1. Формула Ричардсона и правило Рунге

Одним из наиболее распространенных способов экстраполяции является правило Ричардсона, основанное на предположении о справедливости математической модели (4.2) и реальной малости добавочной погрешности.

В этом случае, отбросив малую величину в (4.2), получаем одно уравнение с двумя неизвестными c₁ и z. Чтобы получить второе уравнение, используем другой известный член последовательности . Пусть n₁=n/Q (Q>1), тогда приходим к системе двух уравнений

(4.3)

Отсюда найдем

. (4.4)

С помощью (4.4) определяется экстраполированное (по правилу Ричардсона) значение искомого параметра , а с его помощью находится оценка погрешности приближенного значения z_n

. (4.5)

Этот способ оценки погрешности называется правилом Рунге.

2. Метод Нэвилла

Аналогичный подход имеет место и в случае, когда номер члена последовательности увеличивается на единицу (т.е. n_j+1=n_j+1). Для последовательности {z_n} строится таблица Нэвилла [7,8], представляющая собой матрицу (L=0,1,…, nL+1), в которой нулевой столбец (L=0) – исходная последовательность, а все остальные столбцы находятся по правилу

,

которое получается из рекуррентного соотношения Эйткена при , .

3. Метод численной фильтрации

В более общем случае математическая модель погрешности представляется в виде

, (4.6)

где k₁,…, k_L – произвольные действительные числа (k₁<k₂<…< k_L). Тем не менее, при n_j=n₁Q ^j1 задача определения коэффициентов c_i и экстраполиро­ванного значения z решается аналитически, если применить метод численной фильтрации. Подставив в (4.6) n_j=n₁Q ^j1, получим систему уравнений:

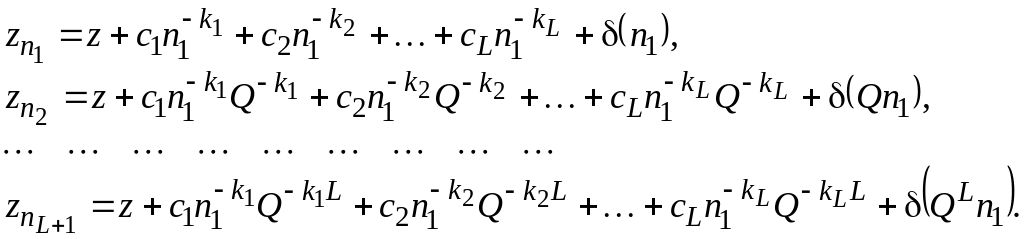(4.7)

Рассмотрим два значения , , вычисленные при числе узлов, равном и соответственно. Составим линейную комбинацию

и потребуем, чтобы суммарный коэффициент при z был равен 1, а при (для определенного j) равен 0. Отсюда получим формулу фильтрации, которая совпадает с Ричардсоновской экстраполяционной .

Критерий качества оценки погрешности

При использовании перечисленных методов оценки погрешности возникает вопрос о допустимости отбрасывания малых (n).

Какой критерий можно для этого применить? Если может быть найдена оценка погрешности оценки погрешности , то отношение этих оценок по модулю должно быть существенно меньше единицы:

.

Это означает, что относительная размытость оценки мала, и такой оценке можно доверять. Если же ¹, то ширина области размытости сравнима с и такую оценку следует отвергнуть.

Поскольку величина получается в виде разности (где экстраполированное значение), то оценкой погрешности величины является оценка погрешности экстраполированного значения (с обратным знаком).

Какая информация может быть использована для получения такой оценки? Мы рассматриваем задачу о нахождении оценок по­грешности в условиях, когда известны только численные значения z_n.

Применим следующий подход. Обозначим экстраполиро­ванное число , полученное с помощью какого-нибудь из изложенных методов при конкретном n. Тогда, увеличивая (или уменьшая) n (в Q, Q², и т.д. в Q^m раз), мы можем получить последовательность уточненных значений . Теперь представим в виде (4.2)

и получим дважды экстраполированное значение , повторив экстраполяцию по Ричардсону по формуле (4.4), (где вместо используем ), или методом Ромберга увеличив L. Разность является искомой оценкой погрешности экстраполиро­ванного значения .

Отметим, что в результате указанных действий получаются дважды экстраполированные значения , погрешность которых также может быть оценена путем повторной (третьей по счету) экстраполяции. Если эта оценка мала по сравнению с , то экстраполированные величины могут быть использованы как уточненные значения с известной оценкой погрешности и мерой ее размытости.

Процесс экстраполяции может повторяться до тех пор, пока очередное отношение ширины области размытости к величине самой оценки не приблизится к 1 или не превысит единицу.

Повторное применение правила Рунге для оценки погрешности результатов вычислений zn при последовательном увеличении n в Q раз называют методом Ромберга.

Результаты экстраполяций удобно представлять в виде треугольной матрицы

Результаты экстраполяций и оценки погрешности удобно представлять на графике в виде зависимости десятичного логарифма относительной погрешности от логарифма n (числа отрезков разбиения). При этом данная зависимость для каждой составляющей погрешности (степенная функция) представлялась бы на таком графике отрезком прямой. Значение ординаты соответствует числу верных знаков.

а)

б)

Рис. 1. Результаты экстраполяции данных, полученных при удвоении числа слагаемых с помощью метода Ромберга: а) – сравнение с эталоном;

б) – оценки по правилу Рунге

Анализ методов экстраполяции с определением порядков аппроксимации

Следует различать задачи по наличию и виду дополнительной (априорной) информации, которая может быть использована при построении математической модели погрешности.

Например, экстраполяция по правилу Ричардсона основана на предположении, что известен порядок точности численного метода (или порядок аппроксимации). В методе Ромберга требуется, чтобы были известны показатели нескольких степенных функций.

Однако при анализе результатов решения сложных задач часто случается, что показатели неизвестны, и их значения должны быть получены из анализа численных результатов.

Метод Эйткена (²-алгоритм)

При оценке погрешности частичных сумм значение k в (4.3) может быть неизвестно. В этом случае можно использовать следующую модификацию правила Ричардсона. Вычислим три значения z₁, z₂, z₃ при трех номерах последователь­ности: n, nQ, nQ² и составим систему трех уравнений

Найдем разности

,

и, разделив одну на другую, определим Q^k:

.

Теперь можно найти z:

.

Как и в рассмотренных ранее случаях, мы нашли экстраполированное (уточненное) значение , а вместе с ним и оценку погрешности .

Этот способ экстраполяции при неизвестном порядке точности принято называть методом Эйткена или ²-алгоритмом, который в более общем случае применяется для экстраполяции векторных последовательностей, например, при решении систем уравнений

.

В последнем выражении z_i – векторы, а скобками обозначается скалярное произведение.

В настоящее время разработано много методов экстраполяции при неизвестном порядке аппроксимации, например, -алгоритм, -алгоритм, u-алгоритм.

1 Эта величина, установленная в [6] экспериментально, впоследствии получила теоретическое обоснование [25].

86