2.3. Интерполяция Постановка задачи

Пусть некоторая функция f(x) задана своими значениями y_j=f(x_j) на дискретном множестве точек x_j., j=0,…,m. Требуется приближенно определить аналитический вид этой функции и тем самым получить возможность вычислить ее значения в промежуточных точках x(x_j,x_j+1). График, иллюстрирующий данную задачу, изображен на рис. 2.3.1.

Рис. 2.3.1. К задаче интерполяции функций.

Интерполирующую функцию будем искать в виде алгебраического многочлена

. (2.3.1)

Поскольку многочлен в узловых точках должен совпадать с заданными значениями функции, то задача сводится к решению системы линейных алгебраических уравнений

относительно неизвестных a_i (k – номер начальной узловой точки, используемой в данном расчете).

Эта система уравнений имеет единственное решение (если mn+k, и все x_j различны). Решение можно представить в форме интерполяционного многочлена Лагранжа:

(2.3.2)

В частном случае n=1

,

а при n=2

.

Нетрудно заметить, что структура этих формул такова, что для каждой узловой точки x=x_j из входящих в набор используемых формулой узловых точек, только одно слагаемое отлично от нуля и именно то, в которое входит y_j. Кроме того, дробь, входящая в это отличное от нуля слагаемое, равна единице. Поэтому .

Теоретическая оценка погрешности интерполяции

, (2.3.3)

где x_j - узлы сетки, .

Для непосредственного применения этой формулы необходимо иметь оценку n+1- й производной функции . Если речь идет об интерполяции известной функции по ее табличным значениям, то такая оценка может быть получена аналитически. Например, производная любого порядка от функций sinx и cosx по модулю не превышает единицы.

Оценка погрешности интерполяции по результатам численного эксперимента

В случае, когда интерполируемая функция является результатом численного решения некоторой задачи, вся информация об искомой функции исчерпывается ее значениями в узловых точках. Задача интерполяции при этом является некорректной, поскольку может существовать сколько угодно функций, проходящих через данные точки (рис 2.3.2). То есть, решение задачи может быть получено только с точностью до произвольной аддитивной составляющей, имеющей нулевые значения во всех заданных узловых точках.

В оправдание этого можно сказать, что если сетка выбирается произвольно, то существование функции, равной нулю именно в узловых точках этой сетки маловероятно. Можно также указать разные способы использования нескольких сеток для повышения надежности получаемых результатов.

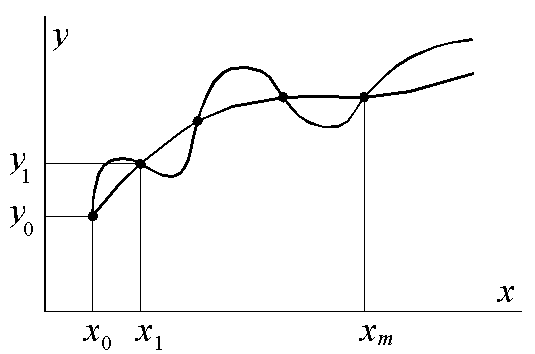
Рис. 2.3.2. Некорректность задачи интерполяции

Мы рассмотрим подход к оценке погрешности интерполяции, не требующий использования никакой другой информации, кроме значений функции в узловых точках.

Для этого на основании (2.3.3) представим математическую модель погрешности интерполяции в следующем виде

. (2.3.4)

Здесь - узлы некоторой сетки; j=0,..., , c - величина, предполагаемая независимой от положения узлов; k₁ - номер начального узла, используемого интерполяционной формулой; ₁(x) - дополнительная часть погрешности, полагаемая малой величиной по сравнению с первым слагаемым.

Теперь заменим сетку, используя новые узлы , j=0,..., . Тогда получим второе уравнение для нахождения неизвестных c и f(x)

. (2.3.5)

Вычитая (2.3.4) из (2.3.5) и пренебрегая малыми, найдем c

, , (2.3.6)

оценку погрешности интерполяции

(2.3.7)

и более точное значение функции

. (2.3.8)

Формировать разные сетки можно различными способами (например, уменьшением шага в 2 раза, выбором закона распределения узлов). В том числе для оценки интерполяции можно использовать значения функции в других узлах той же самой сетки. Последнее может оказаться более удобным с практической точки зрения. Способ выбора узлов также может быть различным.

Рассмотрим случай, когда второй набор состоит из узлов с номерами от k+1 до n+k+1 (т.е. k₁=k, k₂=k+1). В этом случае согласно (2.3.7) погрешность оценивается по формуле

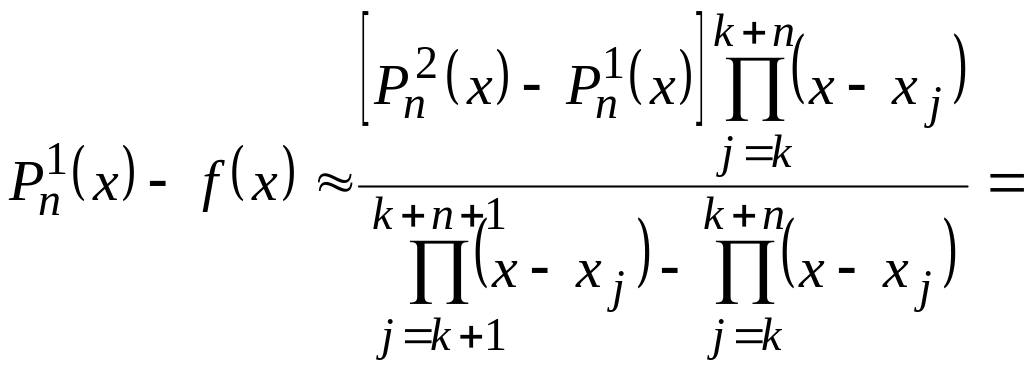
, (2.3.9)

а (2.3.8) принимает вид

. (2.3.10)

Функция (2.3.10) в действительности представляет собой интерполяционный многочлен степени n+1, так как:

- является алгебраическим многочленом степени n+1;

- в узлах с номерами от i=k+1 до i=k+n оба многочлена и , а, следовательно, и , совпадают с ;

- ;

- .

Формула (2.3.10) называется рекуррентным соотношением Эйткена [1].

Таким образом, данный способ оценки погрешности интерполяции сводится к построению интерполяционного многочлена и сравнению проверяемых значений с как с более точными.