МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования «УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра вычислительной математики и кибернетики

Отчет по лабораторным работам

по курсу «Исследование операций»

ИСПОЛЬЗОВАНИЕ

ПАКЕТОВ ПРИКЛАДНЫХ ПРОГРАММ ДЛЯ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Выполнил: студент гр. ПРО-323 Алексеева А.В.

Проверила: Верхотурова Галина Николаевна

Уфа - 2021

Содержание

Введение

1. Постановка задачи (условия задачи)

2. Математическая модель задачи

3. Решение задачи с использованием пакета EXCEL

4. Решение задачи с использованием пакета MathCAD

5. Решение задачи с использованием пакета SciLab

6. Выводы

Заключение

Введение

На практике очень часто возникают задачи, для решения которых используются методы оптимизации.

К таким задачам относятся, например,

• Задачи оптимального планирования деятельности;

• Транспортные задачи;

• Задачи о раскрое;

• Задачи распределения

и многие другие.

В качестве инструмента решения оптимизационных задач используется математическое программирование.

С появлением компьютеров для решения таких задач используются специализированные пакеты прикладных программ, такие как, Excel, Mathcad и Scilab.

Excel – это широко распространенная компьютерная программа.

Представляет собой большую таблицу, в которую можно вносить данные, то есть печатать слова и цифры. Также, используя функции этой программы, можно производить с цифрами разные манипуляции: складывать, вычитать, умножать, делить, совершать консолидацию данных, автоматизировать отчеты, делать сложные массивы данных которые будут автоматически обновляться при грамотном составлении.

Mathcad – программное средство, предоставляющее пользователю инструменты для работы с формулами, числами, графиками и текстами, снабженное простым в освоении графическим интерфейсом.

Scilab — это мощное открытое окружение для инженерных и научных расчётов.

В Scilab реализованы численные методы решения следующих задач вычислительной математики, среди которых можно выделить следующие:

1. задачи линейной алгебры,

2. нелинейные уравнения и систем,

3. задачи оптимизации, при решении которых следует обратить внимание на несколько нестандартный синтаксис,

4. дифференцирование и интегрирование,

5. обработка экспериментальных данных (интерполяция и метод наименьших квадратов),

6. обыкновенные дифференциальные уравнения и системы.

Таким образом, для решения задачи мы будем использовать данные программные продукты.

1. Постановка задачи

На ткацкой фабрике для изготовления ткани трех артикулов используются ткацкие станки двух типов, пряжа и красители. В таблице указаны производительность станков каждого типа, нормы расхода пряжи и красителей, цена 1м такни данного артикула, а также общий фонд рабочего времени станков каждого типа, имеющиеся в распоряжении фабрики фонды пряжи и красителей и ограничения на возможный выпуск тканей данного артикула.

Ресурсы	Нормы затрат на 1м ткани артикула				Общее количество ресурсов
	1		2	3
Производительность станков (станко-ч) 1 типа 2 типа	0,02 0,04		- 0,03	0,04 0,01	200 500
Пряжа (кг)	1,0	1,5		2,0	15000
Красители (кг)	0,03	0,02		0,025	450
Цена 1м ткани (у.е)	5	8		8
Выпуск ткани (м): Минимальный Максимальный	1000 5000	2000 9000		2500 4000

Составить такой план изготовления тканей, согласно которому будет произведено нужное количество тканей данного артикула, а общая стоимость всех тканей максимальна.

2. Математическая модель задачи

Составим математическую модель задачи.

Предположим, что предприятие произведет x1 метров ткани 1-го артикула, x2 метров ткани 2-го артикула и x3 метров ткани 3-го артикула. Тогда задача состоит в определении максимального в стоимостном выражении выпуска ткани

при выполнении следующих ограничений:

• на имеющийся фонд рабочего времени каждого из типов станков:

1 тип:

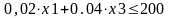
2 тип:

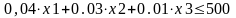
• на выделенные предприятию фонды пряжи и красителей:

Красители:

Пряжа:

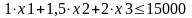
• на возможный выпуск ткани каждого из артикулов:

Окончательно математическая модель задачи оптимизации будет иметь вид:

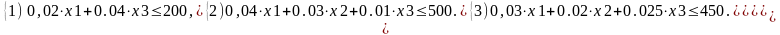
3. Получение оптимального решения в Excel

Для решения задачи я буду использовать Excel, так как эта программа предоставляет отличные возможности для расчетов и решения задачи линейного программирования.

Решать задачу мы будем с помощью инструмента «Поиск решения»

Решим задачу с помощью «Поиск решения» в EXCEL.

В ячейки рабочего листа программного средства вводятся исходные данные и формулы:

• В ячейках В3:D3 будут находиться значения переменных х₁, х₂ и х₃ соответственно

• В ячейки В4:D4 помещаются коэффициенты при переменных в целевой функции задачи.

• В ячейку E4 вводится выражение целевой функции с использованием встроенной функции «СУММПРОИЗВ». Аргументами этой функции являются вышеуказанные массивы ячеек B3:D3 и B4:D4.

• В ячейки В7:D10 помещаются коэффициенты при переменных в ограничениях задачи.

• В ячейки E7:E10 вводятся выражения левых частей ограничений также с использованием функции «СУММПРОИЗВ».

• В ячейках F7:F10 для удобства и наглядности указываются знаки в ограничениях.

• В ячейки G7:G10 вводятся значения правых частей ограничений.

Исходный рабочий лист EXCEL, таким образом, имеет вид:

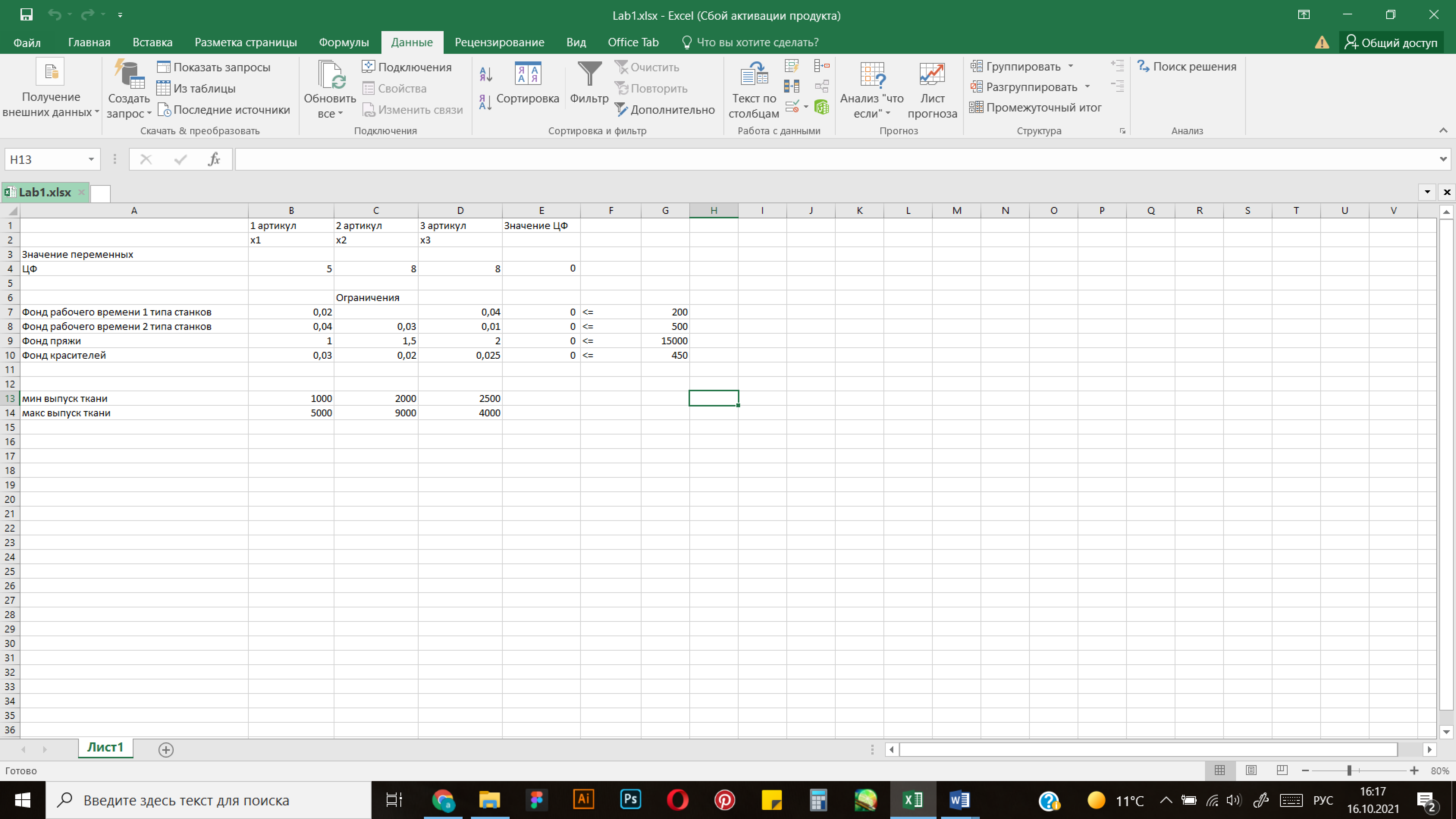
Рисунок 1 Исходный рабочий лист

Для решения задачи оптимизации запускается надстройка «Поиск решения» (меню «Данные») и заполняются все необходимые поля в панели надстройки:

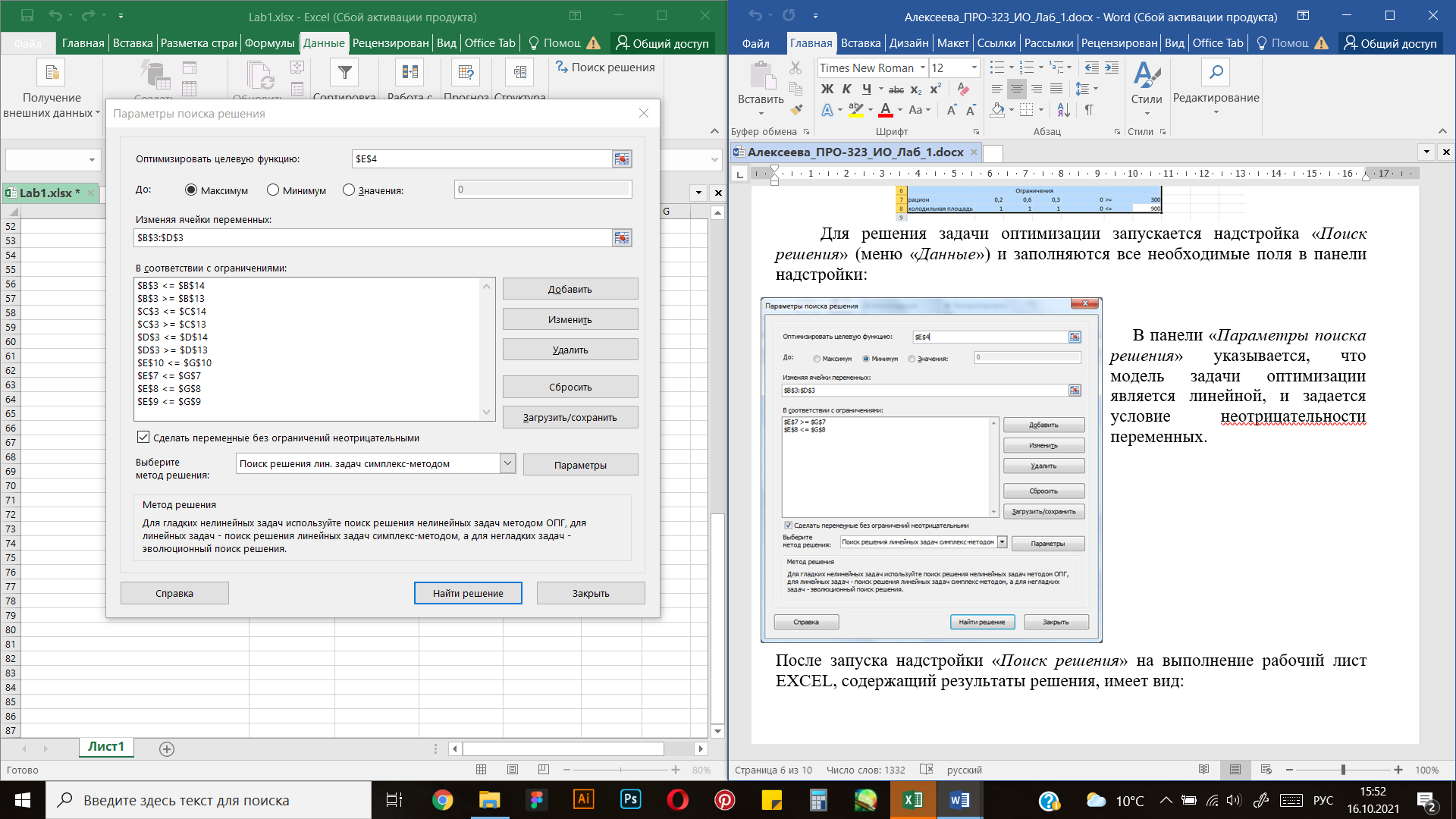
Рисунок 2 Надстройка "Поиск решения"

В панели «Параметры поиска решения» указывается, что модель задачи оптимизации является линейной, и задается условие неотрицательности переменных.

После запуска надстройки «Поиск решения» на выполнение рабочий лист EXCEL, содержащий результаты решения, имеет вид:

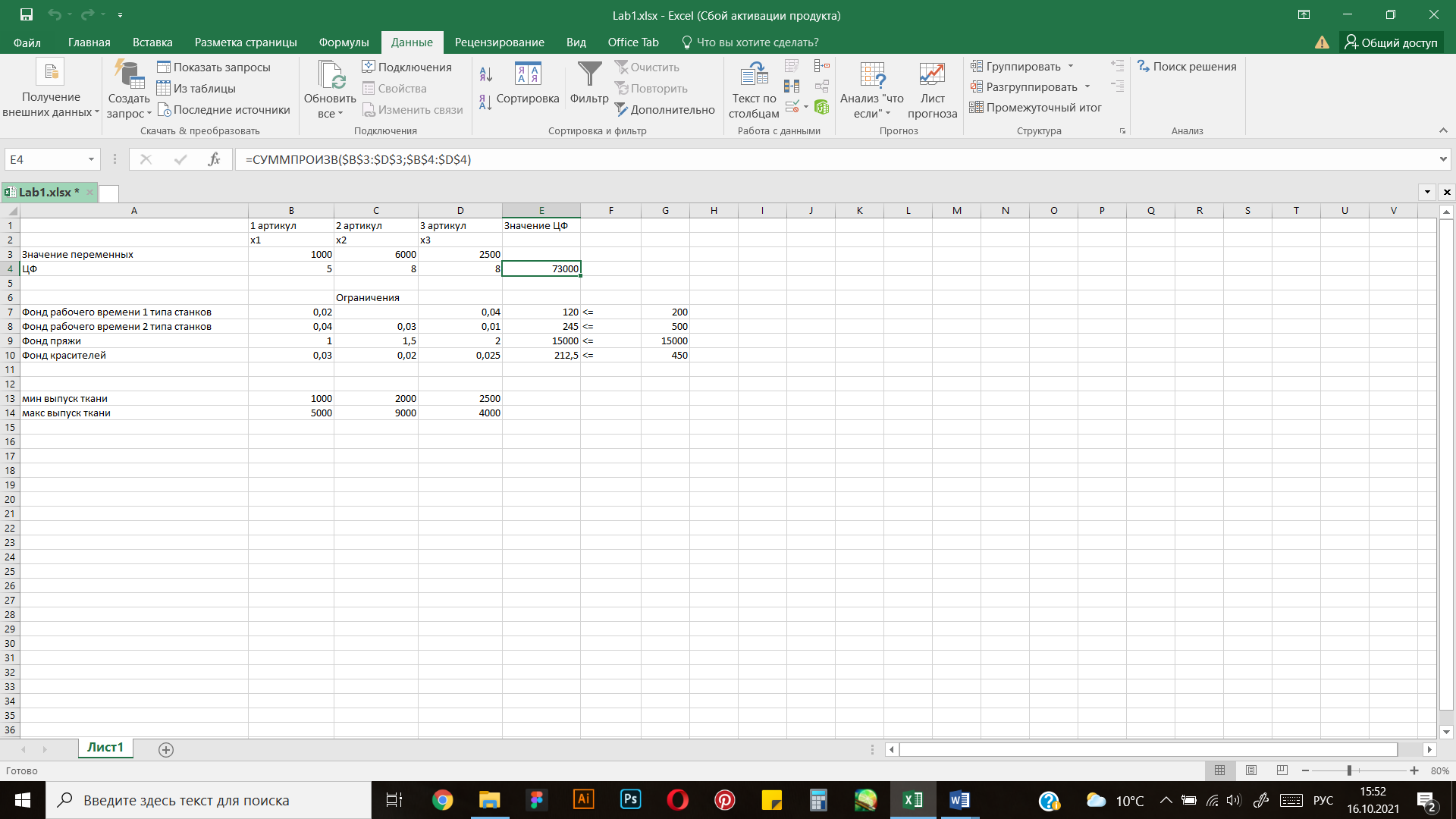
Рисунок 3 Результат

Таким образом, получили следующее решение: для того, чтобы общая стоимость тканей была максимальной (73000), нужно произвести 1000м ткани 1 артикула, 6000м ткани 2 артикула и 2500м ткани 3 артикула.