11.Peremennye_tsepi_1F_VSYo

Добавил:

Kupac Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

Основы электротехники и электроники

Файл:

j LI m j X L I m Z L I m

.pdf

Скачиваний:

Добавлен:

19.11.2022

Размер:

518.47 Кб

Скачать

☆

Коваленко В.Е. ноябрь 2021г. ОЭиЭ

Метод комплексных амплитуд (символический метод)

1.Комплексные числа и основные операции над ними

Символический метод комплексных амплитуд (символический метод) основан на представлении гармонических функций времени a t в форме комплексных чисел.

Напомним, что комплексным числом A (обозначаем подчёркиванием) называется выражение вида

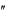A A jA Ae j ,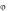

которое на комплексной плоскости отображается в виде точки с абсциссой A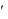 (вещественная часть) и ординатой A 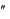(мнимая часть) (рис. 2.2, а).

Ось абсцисс, по которой откладывается вещественная часть A , называется действительной ( Re ), а ось ординат, по которой откладывается мнимая часть A , — мнимой ( Im ).

Каждой точке A комплексной плоскости может быть(2поставлен.8) в соответствие вектор A (рис. 2.2,б). Длину вектора A называют его модулем

	A	A 2	A 2 ,

а угол , образуемый вектором A с положительным направлением вещественной оси, на-
зывают аргументом комплексного числа			(2.9)
		arctg	A	.

			A

Вещественную и мнимую части комплексного числа можно определить через модуль и аргумент:

а)

б)

Рис. 2.2

Re A

cos

;

(2.10)

Im A

sin

Подставляя далее (2.10) в выражение (2.7), можно перейти от алгебраической записи

комплексного числа к тригонометрической:

cos

(2.11)

sin .

Далее, используя формулу Эйлера

e j

cos

j sin

получаем показательную форму комплексного числа:

e j .

(2.12)

2. Комплексные изображения гармонических функций

Каждой гармонической функции a t можно поставить в соответствие комплексное число A , называемое мгновенным комплексом гармонической функции:

A Am e	j t	Am cos t	j sin t	(2.13)

модуль которого равен амплитуде гармонической функции Am , а аргумент — ее фазе

Значение мгновенного комплекса A при t

0 называется комплексной амплитудой

A e j

(рис. 2.1).

С использованием понятия комплексной амплитуды выражение для мгновенного ком-

плекса может быть преобразованно к виду

A Am e

Am e

(2.14)

где e j t ,

называемый оператором вращения,

имеет единичную длину и вращается в ком-

плексной плоскости против часовой стрелки со скоростью

(рис. 2.2). Всякий неподвиж-

ный вектор,

будучи умноженным на e j t , начинает вращаться против часовой стрелки с

угловой скоростью .

Пример 2.1. Комплексная амплитуда гармонического тока i 5sin

103 t

равна

5 e j

50sin 105 t —

а комплексная амплитуда гармонического

напряжения u

50 e j 0

50 .

Основные действия с комплексными изображениями гармонических функций. При сложении (вычитании) комплексных чисел их записывают в алгебраической форме и отдельно складывают (вычитают) их действительные и мнимые части. Например, если

	A		A e j	A cos	jA sin	A	j A	,
		1	1	1	1	1	1
A		2	A e j	A cos	jA sin	A	j A	,
		2	2	2	2	2	2

то

A A

j A

Ae j ,

где A

A1 A2

arctg

Умножение и деление комплексных величин производят, как правило, в показатель-

ной форме:	A A		A A e j		;	A1	A1	e j .
ной форме:	A A	2	A A e j		;			e j .
	1	2	1	2		A2	A2
						A2	A2

В комплексной форме дифференцирование по времени соответствует умножению, а интегрирование — делению комплексных значений рассматриваемых функций на j ,

поэтому

uC	1	i dt	1	I m	j X C I m Z C I m	U	Cm ,
	C		j C			U

где X L		и X C — индуктивное и емкостное сопротивления; Z L и Z C — соответственно
индуктивное и емкостное сопротивления в комплексной форме.
	Для резистивного элемента напряжение в комплексной форме
			uR R i	RI m Z R I m U Rm ,
где Z R		R — вещественная величина.

Замечание. Часто в практических расчетах удобно пользоваться действующими значе-

ниями величин, тогда U R Z R I , U L Z L I , U C Z C I .

Пример 2.2. Определить эквивалентное комплексное сопротивление двухполюсника

R	R
L	jXL
L
C	-jXC
а)	б)
	Рис. 2.3

относительно входных зажимов (рис. 2.3,а).

Решение. Комплексное сопротивление схемы замещения электрической цепи (рис. 2.3,

б):

jX C

Пример 2.3. К зажимам идеализированного пассивного элемента (рис. 2.4) приложено

напряжение U

0,36e j 74

мВ. Определить тип и параметры элемента Z , если значение

тока: а) I

2,4 e j 74 мкА;

б) I

2,4e j164

мкА;

в)

2,4e j 344

мкА.

Решение. Значение параметра элемента Z

а) Z

0,15e j 0 кОм; б) Z

0,15e j 90

кОм;

в)

0,15e j 90

кОм.

Если сдвиг фаз между напряжением и током на элементе равен 0,

или

, то такой

элемент будет соответственно резистивным, индуктивным или емкостным.

U Z

Рис. 2.4

Пример 2.4. Выразить входное сопротивление и ток последовательной RLC-цепи (рис.

2.5,а) в комплексной форме для частот		1	2,5 106 c 1 ,		2	8 106 c 1 ,	3	5 106	c 1 .
		1			2		3
Параметры	цепи: L 80 мкГн, C	500 пФ,		R 100 Ом.		Входное		напряжение

u 10 2 cos	t.

Решение. Комплексное входное сопротивление по (2.16) равно сумме комплексных сопротивлений элементов цепи. Подставляя в (2.16) параметры элементов, находим:

j 80,5

Z 1

100

j 600

608e

Ом;

403e j 75,6 Ом;

Z 2

100

j 390

Z 3

100 Ом.

Таким образом, при

входное сопротивление имеет резистивно-емкостный ха-

рактер, при

2 — резистивно-индуктивный, а при

3 — чисто резистивный ха-

рактер.

Используя закон Ома в комплексной форме, находим:

I 1

16,4 e j 80,5 мА;

608e

j 80,5

I 2

24,8e j 75,6

мА;

I 3

100 мА.

100

402,6 e j 75,6

Здесь I 1 опережает входное напряжение на 80,5 ,

I 2

отстает от напряжения на 75,6 , I 3

совпадает по фазе с напряжением.

Пример 2.5. В цепи (рис. 2.10) напряжения на соответствующих индексам элементах

и ток I 1

имеют следую-

щие

значения:

R 1

I 1

U R1

2,33e149,8

В;

I 2

R 2

6,93 e

210,5

В;

4,66e239,8

R 2

В;

0,77 e120,5

В;

6,97 e24,2 В;

2,33e144,8 А.

I 1

Рис. 2.10

Проверить

выполнение

баланса мощностей.

Решение. В соответствии с условием баланса мощностей мощность источников равна

мощности потребителей: S и

S п .

S и

E I 1

J J

21,5 j9,06 10 3 В А ;

I 2

j X

I 2

j X

21,4

j9,07 10 3 В А .

Условие баланса выполняется.

3. Преобразования электрических цепей

Понятие об эквивалентных преобразованиях. Анализ процессов в электрических цепях может быть существенно упрощен за счет использования различных преобразований, в результате которых отдельные участки цепей заменяются эквивалентными — либо с более простой топологией, либо более удобными для анализа.

Два участка цепи называются эквивалентными, если при замене одного из этих участков другим токи и напряжения в остальной части цепи не изменятся. Преобразования такого типа также называются эквивалентными. Отметим, что преобразуемые электрические цепи должны иметь одинаковое число внешних выводов, и в процессе преобразований токи выводов и напряжения между ними должны оставаться неизменными.

Рассмотрим правила преобразования цепей с последовательным и параллельным соединениями.

Участки цепи с последовательным соединением элементов. Рассмотрим однокон-

турную цепь (рис. 2.11). Уравнение этой цепи составим по второму закону Кирхгофа для мгновенных значений:

R i	R	i	1	i dt	1		i dt L	di	L		di
R i	R	i		i dt			i dt L		L	k dt
1	n		C		C	m	1 dt			k dt
			1			m

		u	e	e	p	. (2.34)
			1		p
После приведения подобных (2.34) примет вид:
i R 1	R n	C 1	C m	i		R э
						C э
u		L 1		u
e p	e 1					L	э
e p	e 1	L k			e э
		L k
	а)				б)		5
	а)				б)
		Рис. 2.11

i dt

u (2e.35),

CЭ

Э dt

m 1

где

;

; e

e .

CЭ

i 1 Ci

i 1

Если обобщенная одноконтурная цепь находится под гармоническим воздействием, то от эквивалентной схемы (рис. 2.11) удобнее перейти к электрической схеме для комплексных значений (рис. 2.12, а). Уравнения (2.34) в комплексной форме в этом случае имеют вид:

Z R1 I 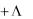Z R n I Z C 1 I 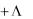Z C m I Z L1 I 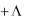Z L k I

	U	E1	E p .(2.36)

После преобразований:

			Z Э I	U EЭ ,
n		m	k	p
где Z Э	Z R i	Z C i	Z L i ; E Э	E i .
i 1		i 1	i 1	i 1

Эквивалентная цепь для комплексных действующих значений приведена на рис. 2.12,

б.

I Z R 1	Z R n	Z C 1			I
			Z C m		Z э
U				U	Z э
U				U
E p	E 1		Z L 1		E э
E p	E 1	Z L k			E э
		Z L k
	а)				б)
		Рис. 2.12

Участки цепи с параллельным соединением элементов. Пусть электрическая цепь

(рис. 2.13, а) состоит из параллельно соединенных n активных сопротивлений, m емкостей, k индуктивностей и p независимых источников тока (обобщенная двухузловая цепь). Все элементы цепи находятся под одним и тем же напряжением u, поэтому уравнение цепи, по первому закону Кирхгофа

u C

(2.37)

u dt

J p .

После приведения подобных

u dt(2.J38),

RЭ

Э dt

LЭ

где

;

; C

;

LЭ

i 1 Li

i 1

Уравнению (2.38) соответствует преобразованная цепь (рис. 2.13, б).

При гармоническом воздействии для комплексной схемы замещения (рис. 2.14, а, б, в)

I Y R1	U		Y R n	U		Y C 1	U	Y C m	U

Y L1		U	Y L k		U	J 1		J p .

После преобразований:

			I	Y Э U J Э , (2.39)
n		m	k	p
где Y Э	Y R i	Y C i	Y L i ; J Э	J i .
i 1		i 1	i 1	i 1

	R n	C 1	C m		J1	Jp
	R n
	R 1
u	R 1			L 1	L k
			а)
	i
	R э	C э
u	R э		L э	J э

б)

Рис. 2.13

Эквивалентные преобразования треугольника сопротивлений в звезду и звезды — в треугольник.

Такие преобразования должны быть эквивалентными по отношению к внешней цепи. Это значит, что подходящие к выводам токи должны быть одинаковы, одинаковы также должны быть напряжения между выводами, т. е. I 1 , I 2 , I 3 и U 12 , U 2 3 , U 31 одинаковы

как для звезды (рис. 2.15, а), так и для треугольника (рис. 2.15, б) сопротивлений. Соотношения эквивалентности для комплексных значений при переходе от треуголь-

ника к звезде:

Z 1		Z 12	Z 31	;	Z 2	Z 12	Z 2 3	;
	Z 12	Z	2 3 Z 31			Z 12 Z 2 3 Z 31

			Z 3		Z 2 3 Z 31		.	(2.40)
			Z 3	Z 12	Z 2 3	Z 31	.
				Z 12	Z 2 3	Z 31
	I
		Y R n	Y C m			Y L k	J1	Jp
							J1	Jp
U	Y R 1	Y C 1		Y L 1

			а)
	I				I
		Y L э			Y э
U	Y R э	Y C э	J э	U	J э
		б)			в)
			Рис. 2.14

		I 1					I 1
			1				1
	U 3 1			U 1 2	U 3 1		Z 1	U
					U 3 1
			Z 1 2
			Z 1 2
		Z 3 1						Z 2
								Z 2
		Z 2 3			Z 3
		Z 2 3		I 2
I 3				I 2	I 3	3	2 I
I 3	3			2	I 3	3	2 I
	3			2
		U 2 3					U 2 3
			а)				б)

Рис. 2.15

1 2

При переходе от звезды к треугольнику:

Z 12	Z 1 Z 2	Z 1 Z 2	; Z 2 3	Z 2 Z 3	Z 2 Z 3	; Z 31	Z 3 Z 1	Z 3 Z 1	.	(2.41)

		Z 3			Z 1			Z 2

Выражения комплексных проводимостей, образующих стороны треугольника, могут быть получены из (2.41) путем замены комплексных сопротивлений их проводимостями:

Y 12		Y 1 Y 2		; Y 2 3			Y 2 Y 3	;
	Y 1	Y 2 Y 3				Y 1 Y 2 Y 3
		Y 31		Y 3 Y 1			.
			Y 1	Y 2
					Y 3

Пример 2.6. Рассчитать комплексное входное сопротивление цепи (рис. 2.16). Параметры цепи:

1кОм ;

R 1

C 1

L 1

С1

С2

0,5 нФ ;

10 мГн ; f

39,8 кГц .

C 2

Решение.

Эквивалентное

комплексное

сопротивление

ветви R1

Z Э 1

Z R1

Z L

Z C 1 .

Комплексное

сопротив-

ление параллельно включен-

Рис. 2.16

ных ветвей с Z Э 1 и C2

Z Э 2

Z Э 1 Z C 2

Z Э 1

Z C 2

Комплексное входное сопротивление цепи

Z В Х

Z R 2

Z Э 2 .

В этих выражениях

Z R1 Z R 2 R , Z L

j L , Z C 1

Z C 2

Подставив значения параметров элементов цепи, получим:

Z В Х 1 кОм.

Решаем задачу на занятие.

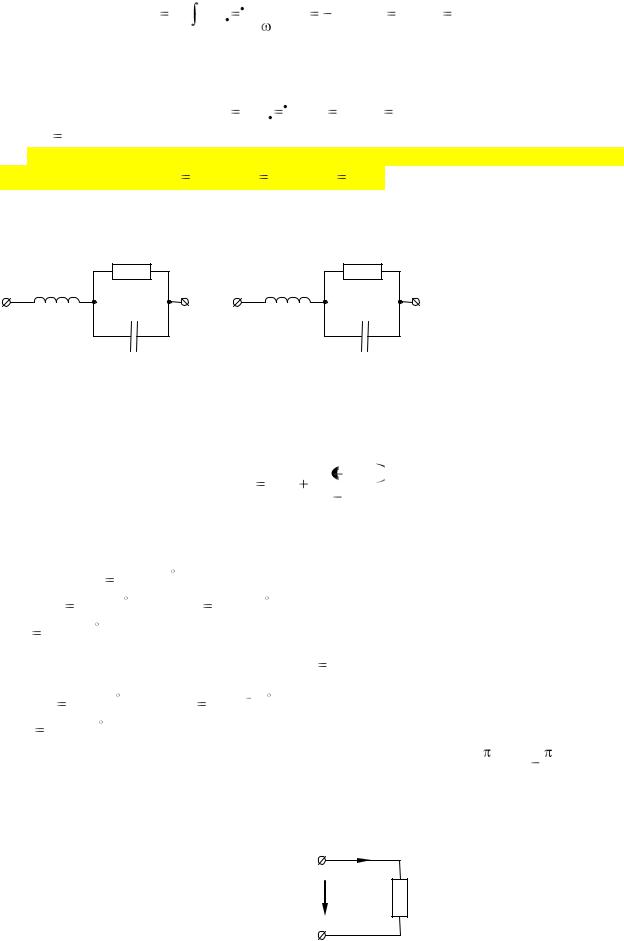
1) Определить токи i(t), i1(t), i2(t) в ветвях для схемы ниже, если R=8 Ом, R2=4 Ом,

X1=6 Ом, X2=3 Ом, u(t)= (50√2 Sin (ωt) ) В , f=50

Гц. Определить параметры L и C.

Дорешать задачу 1 до конца самостоятельно.

Самостоятелно решить задачу.

Дано R= 10 Ом, R2=4 Ом, XL=3 Ом, XC=6 Ом, u(t)= (141 Sin (628t) ) В.

Определить токи i(t), i1(t), i2(t) в ветвях для схемы ниже.

I R

Соседние файлы в предмете Основы электротехники и электроники

#
19.11.2022582.1 Кб2306.laboratornaya_OR.pdf
#
19.11.2022608.52 Кб1207.SDO_520_LR1_Rasch_LETs_post_toka.pdf
#
19.11.2022489.43 Кб3608.LEKTsIYa_3_1ch_Perem_tok_1za_1vn.pdf
#
19.11.20221.03 Mб4709.LEKTsIYa_4_RLC_tsep_MKA_Moschnost_TsPT_Balans.pdf
#
19.11.2022607.09 Кб5910.Lektsia_5_i_6_Rezonans.pdf
#
19.11.2022518.47 Кб3211.Peremennye_tsepi_1F_VSYo.pdf
#
19.11.2022729.57 Кб4312.Lektsia_7_ISTs_s_primerom.pdf
#
19.11.2022656.78 Кб4113.Tryokhfaznye_tsepi.pdf
#
19.11.20221.09 Mб3014.Chetyryokhpolyusniki_10_2021.pdf
#
19.11.2022357.35 Кб3415.Perekhod_prots_Klassich_Metod.pdf
#
19.11.2022247.65 Кб2716.L11_Klas_prod.pdf