3. Расчет гидродинамических коэффициентов сопротивления волновых нагрузок

Цель работы:

1. Обработка экспериментальных данных (лаб. работа №2).

2. Изучение основных положений методики расчета гидродинамических коэффициентов сопротивления волновых нагрузок, базирующихся на линейной теории волн.

3. Расчет гидродинамических коэффициентов сопротивления волновых нагрузок для заданного варианта.

Обработка экспериментальных данных лабораторной работы №2:

Решение:

1. Рассчитаем период и высоту волны:

 = X_T / К_T = 10,9 / 10 = 1,09 с;

h = y_V·к_V = 56,1·0,0013 =0,073 м

2. В момент времени t₁ (на вершине волны) будет присутствовать только скоростная составляющая волновой нагрузки, поскольку ускорения частиц жидкости в этот момент равны нулю. Следовательно:

- амплитудное значение скоростной составляющей волновой нагрузки в верхнем датчике

q_cb = y_b1·k_b = 1,1·0,00945 = 0,011 H;

- амплитудное значение скоростной составляющей волновой нагрузки в нижнем датчике

q_ch = y_h1·К_H = 0,31·0,0042 = 0,0013 H

В момент времени t₂ (на склоне волны) будет присутствовать только инерционная составляющая волновой нагрузки, поскольку скорости частиц жидкости в этот момент равны нулю. Следовательно:

- амплитудное значение инерционной составляющей волновой нагрузки в верхнем датчике

q_ив = Y_B2·K_B = 29,32·0,00945 = 0,278 Н;

- амплитудное значение инерционной составляющей волновой нагрузки в нижнем датчике

q_ин = Y_Н2·K_Н = 34,5·0,0042 = 0,145 Н;

Определим отношения величин нагрузок в верхнем и нижнем датчиках:

q_cb / q_cн = 0,011 / 0,0013 =8,46; q_ив / q_ин = 0,278 / 0,145 =1,92.

3. Предварительно определим следующие параметры волнового движения:

- круговая частота волны  = 2 /  =23,14/1,09 =5,76 с^-1;

- волновое число k = ² / g = 5,76²/9,81 =3,38 м^-1;

- длина волны  = 2 / k =2·3,14/3,38 = 1,86 м;

- амплитудное значение скорости горизонтального орбитального движения частиц жидкости на уровне верхнего датчика

м/с

- амплитудное значение скорости горизонтального орбитального дви­жения частиц жидкости на уровне нижнего датчика

м/с

- амплитудное значение ускорения горизонтального орбитального движения частиц жидкости на уровне верхнего датчика

м/с²;

- амплитудное значение ускорения горизонтального орбитального движения частиц жидкости на уровне нижнего датчика

м/с².

4. Определяем гидродинамические коэффициенты сопротивления:

- скоростной составляющей волновой нагрузки для верхнего датчика

- скоростной составляющей волновой нагрузки для нижнего датчика

- инерционной нагрузки для верхнего датчика

- инерционной нагрузки для нижнего датчика

5. Для сопоставления полученных результатов с литературными данными, определим значения числа Кьюлегена - Карпентера N_кс:

- для верхнего датчика N_ксв = V_в·/D = 0,126·1,09/0,076 = 1,81;

- для нижнего датчика N_ксн = V_н·/D = 0,0602·1,09/0,076 = 0,863;

6. Используя величины N_ксв и N_ксн, по графику на рис. 4 находим "литературные" значения коэффициентов волновых нагрузок:

С_свл = 0,45; С_снл = 0,25; С_ивл = 2,3; С_инл = 2,45;

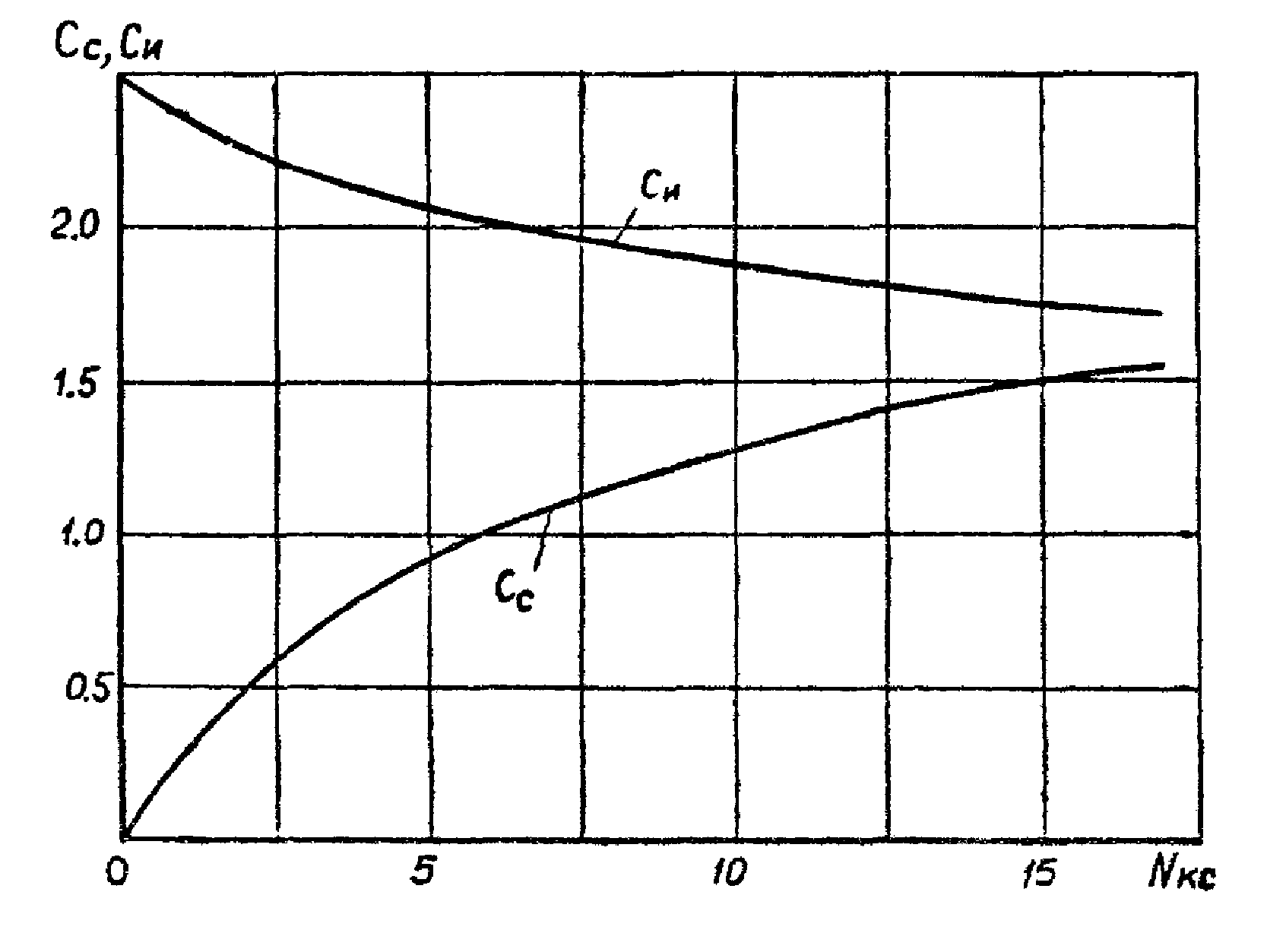
Рис.7. Зависимость коэффициентов С_с и С_и от числа Кьюлегена-Карпентера

Составим соотношения:

; ; ;
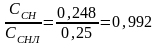