
S
.rtf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По
таблице №1 строим зависимости μ(T),
Cp(T),
Pr(T).
И находим
 ,
,
 ,
,
 ,
,
 ,
,
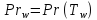 ,
,
 .
.
Определяем температуры и энтальпии восстановления газа на адиабатической стенке и в выбранных сечениях сопла: T∞ = Ti,
Температура
восстановления

Температура
стенки
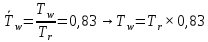
Где
 – коэффициент восстановления.
– коэффициент восстановления.
 ,
,
 – энтальпии
при температурах восстановления и
стенки.
– энтальпии
при температурах восстановления и
стенки.
2. Определяем коэффициенты теплообмена в выбранных сечениях сопла.
Плотность
продуктов сгорания при температуре
стенки:

Число
Рейнольдса:

s – длина сопла по контуру, определяем графически, измеряя длину кривой от КС до расчетного сечения.
Определим значение чисел Статона:

Для учета шероховатости и конденсированной фазы вводятся коэффициенты kш и kр.

 ,
где A,
m,
n
– коэффициенты, A
= 0,0246, m
= -0,3, n
= 2,45;
,
где A,
m,
n
– коэффициенты, A
= 0,0246, m
= -0,3, n
= 2,45;
Z – содержание к-фазы в продуктах сгорания, Z=0,35
Число
Стантона с учетом поправочных
коэффициентов:

Коэффициент
теплоотдачи:
 .
.
Результат расчетов приведен в таблице №3.
Таблица №3.
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По результатам расчёта строим график зависимости коэффициента α от S:
По полученным значениям видно, что самым теплонагруженным является критическое сечение, поэтому решено сделать его из тугоплавкого металла, в данном случае применен вольфрам. Длина «ленточки» трансзвуковой части сопла выбирается с учетом технологических и эксплуатационых требований. Для того, чтобы выполнить отверстие диаметром dкр наличие «ленточки» является необходимым и отвечает требованиям технологичности конструкции. Кроме того, в процессе работы РДТТ при наличии острой кромки критического сечения происходил бы её разгар практически с первых секунд работы двигателя. Это привело бы к падению давления в камере, снижению тяги и появлению экстриситента. Поэтому с целью избежания указанных эффектов трансзвуковую часть сопла изготавливают в виде цилиндрической образующей. Однако «ленточка» не должна быть слишком длинной, поскольку в этом случае увеличиваются габаритно-массовые характеристики сопла и повышается вероятность осаждения к-фазы на входе в трансзвуковую часть сопла. Кроме того применены следующие материалы: углепластик для внутренней поверхности расширяющей части и крепления эластичного опорного шарнира, углрод-углеродный композитный материал для сужающейся части («воротник»), а также высокоплотный графит в сужающейся части сопла перед критикой.
Затем
по формуле
 определяем конвективный тепловой поток
в каждом сечении (результаты приведены
в таблице №5).
определяем конвективный тепловой поток
в каждом сечении (результаты приведены
в таблице №5).
Определение лучистого теплового потока.
Топливо обусловлено в первую очередь содержанием в них водяных паров и углекислого газа.
Радиационный тепловой поток от газов к стенке определяется по формуле:
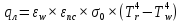
Где
εпс
– эффективная интегральная излучающая
способность (степень черноты) стенки и
продуктов сгорания ; εw
= 0,8 – эффективная степень черноты
стенки; σ0
= 5,67•10-8
Вт/(м2•T4)
– постоянная Стефана-Больцмана.
Из
результатов расчета термодинамических
параметров (см. Приложение №1) парциальные
давления:
 ,
,
 .
.
Длина
пути луча:

Степень черноты смеси газов H2O и CO2:

Степень
черноты H2O
:

Давление в камере сгорания – pk = 4 Мпа. Внутренний диаметр канала dв = 0,07 м, наружный диаметр заряда – dв = 0,35 м, радиус скругления щели – rщ = 0,001 м, длина заряда – L = 1 м, длина щелевой части – Lщ = 0,33 м. Оба торца заряда свободны, поскольку используются передняя и задняя раскрепляющие манжеты. В качестве примера зададимся следующими характеристиками смесевого топлива. Плотность топлива – ρт = 1500 кг/м3, предел прочности топлива на растяжение – [σв.р] = 5 Мпа, модуль упругости топлива – E = 20 Мпа, коэффициент Пуассона – μ = 0,4, температурный коэффициент топлива линейного расширения топлива – αт = 0,9•10-4 К-1, равновесная и предельно допустимая температуры эксплуатации – Т0 = 20°С, Т1 = 50°С. Величину предельной относительной деформации можно рассчитать по формуле

А. Напряжения при нагружении заряда внутрекамерным давлением.
Безразмерный
радиус:

Давление на внешней поверхности заряда рассчитаем по зависимости:

Напряжения на внешней поверхности заряда:
-
радиальные

-
тангенциальные
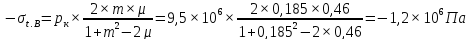
Напряжения на внутренней поверхности заряда:
-
радиальные

-
тангенциальные
Для внутренней поверхности топлива рассчитаем возникающие деформации.
Деформация
внутренней поверхности канального
заряда
 :
:

Выбираем
далее по номограммам коэффициент
разгрузки
 :
:
Для
 и
и
 величина
величина

Таким образом, величина кольцевой деформации канала будет равна:
 .
.
Так как εt.A = 0,24≤0,25, то условие прочности выполняется.
Определим деформацию основание щели с учетом коэффициентов нагрузки.
