Сравнение методов расчета оптимальной цены
|
|
pопт.2 |
pопт.1 |
|
10 |
98,24 |
100 |
|
30 |
108,24 |
100 |
|
50 |
118,24 |
100 |
|
70 |
128,24 |
100 |
|
100 |
143,24 |
150 |
|
120 |
153,24 |
150 |
p0
Проанализируем результаты, представленные в табл. 2 и 3.
Согласно табл.2, при расчете восстановленной функции D*(p) при p = 200 получаем отрицательную величину (-5,18), что не имеет смысла, т.к. спрос не может быть отрицательным. Рассмотри ситуацию подробнее. Функция спроса убывает, коэффициент a* отрицателен, поэтому рано или поздно прямая уйдет в отрицательную область. Это значит, что приближение функции спроса линейной зависимостью может быть корректно лишь на некотором отрезке, а не на всей прямой. Выясним, при какой цене спрос достигает 0:
D*(p) = (-0,38362)p +71,54 = 0,
p
=
= 186,5.
Т.е. корректное приближение функции спроса линейной зависимостью может быть при цене p меньшей, чем 186,5 рублей.
Общепринятых простых методов, позволяющих избежать отрицательных оценок функции спроса, нет. Если получаем отрицательные величины, то должны указать область, в которой линейная зависимость дает корректную оценку, что и сделали выше, когда D*(p) приравняли к 0.
Рассмотрим теперь табл.3. Здесь видим разницу между расчетной оптимальной ценой pопт.2, полученной с помощью метода наименьших квадратов, и расчетной ценой pопт.1, найденной исходя только из данных опроса. Это связано с тем, что потребитель всегда склонен к круглым числам (например, большинство назовет 100 руб., а не 102 руб. 27 коп.). Мы же при применении метода наименьших квадратов ищем максимум не только среди названных опрощенными значений, а по более обширному множеству.
4. Альтернативный метод расчета
Можно построить таблицу (метода наименьших квадратов) и провести все расчеты и без указания частот цен, т.е. чисел, показывающих, сколько раз названа та или иная цена. При таком подходе необходимо все данные ввести в таблицу в порядке неубывания, т.е. все 50 значений, а далее произвести расчеты аналогично предыдущему примеру (табл.4).
Таблица 4
Альтернативный метод расчета оценок параметров
|
i
|
pi |
D(pi) |
D(pi)pi |
(pi)2 |
а*(pi) |
D*(pi) |
D(pi)-D*(pi) |
[D(pi)-D*(pi)]2 |
|
|
50 |
50 |
2500 |
2500 |
-19,1812153 |
52,3587847 |
-2,35878472 |
5,56386535 |
|
|
50 |
50 |
2500 |
2500 |
19,1812153 |
52,3587847 |
-2,3587847 |
5,56386526 |
|
|
60 |
48 |
2880 |
3600 |
-23,0174583 |
48,5225417 |
-0,52254166 |
0,27304979 |
|
|
60 |
48 |
2880 |
3600 |
23,0174583 |
48,5225417 |
-0,52254166 |
0,27304979 |
|
|
75 |
46 |
3450 |
5625 |
-28,7718229 |
42,7681771 |
3,231822923 |
10,4446794 |
|
|
75 |
46 |
3450 |
5625 |
-28,7718229 |
42,7681771 |
3,231822923 |
10,4446794 |
|
|
75 |
46 |
3450 |
5625 |
-28,7718229 |
42,7681771 |
3,231822923 |
10,4446794 |
|
|
75 |
46 |
3450 |
5625 |
-28,7718229 |
42,7681771 |
3,231822923 |
10,4446794 |
|
|
75 |
46 |
3450 |
5625 |
-28,7718229 |
42,7681771 |
3,231822923 |
10,4446794 |
|
|
75 |
46 |
3450 |
5625 |
-28,7718229 |
42,7681771 |
3,231822923 |
10,4446794 |
|
|
75 |
46 |
3450 |
5625 |
-28,7718229 |
42,7681771 |
3,231822923 |
10,4446794 |
|
|
75 |
46 |
3450 |
5625 |
-28,7718229 |
42,7681771 |
3,231822923 |
10,4446794 |
|
|
90 |
38 |
3420 |
8100 |
-34,5261875 |
37,0138125 |
0,986187507 |
0,9725658 |
|
|
90 |
38 |
3420 |
8100 |
-34,5261875 |
37,0138125 |
0,986187507 |
0,9725658 |
|
|
90 |
38 |
3420 |
8100 |
-34,5261875 |
37,0138125 |
0,986187507 |
0,9725658 |
|
|
90 |
38 |
3420 |
8100 |
-34,5261875 |
37,0138125 |
0,986187507 |
0,9725658 |
|
|
100 |
34 |
3400 |
10000 |
-38,3624306 |
33,1775694 |
0,822430563 |
0,67639203 |
|
|
100 |
34 |
3400 |
10000 |
-38,3624306 |
33,1775694 |
0,822430563 |
0,67639203 |
|
|
100 |
34 |
3400 |
10000 |
-38,3624306 |
33,1775694 |
0,822430563 |
0,67639203 |
|
|
100 |
34 |
3400 |
10000 |
-38,3624306 |
33,1775694 |
0,822430563 |
0,67639203 |
|
|
100 |
34 |
3400 |
10000 |
-38,3624306 |
33,1775694 |
0,822430563 |
0,67639203 |
|
|
100 |
34 |
3400 |
10000 |
-38,3624306 |
33,1775694 |
0,822430563 |
0,67639203 |
|
|
100 |
34 |
3400 |
10000 |
-38,3624306 |
33,1775694 |
0,822430563 |
0,67639203 |
|
|
100 |
34 |
3400 |
10000 |
-38,3624306 |
33,1775694 |
0,822430563 |
0,67639203 |
|
|
100 |
34 |
3400 |
10000 |
-38,3624306 |
33,1775694 |
0,822430563 |
0,67639203 |
|
|
100 |
34 |
3400 |
10000 |
-38,3624306 |
33,1775694 |
0,822430563 |
0,67639203 |
|
|
100 |
34 |
3400 |
10000 |
-38,3624306 |
33,1775694 |
0,822430563 |
0,67639203 |
|
|
100 |
34 |
3400 |
10000 |
-38,3624306 |
33,1775694 |
0,822430563 |
0,67639203 |
|
|
100 |
34 |
3400 |
10000 |
-38,3624306 |
33,1775694 |
0,822430563 |
0,67639203 |
|
|
100 |
34 |
3400 |
10000 |
-38,3624306 |
33,1775694 |
0,822430563 |
0,67639203 |
|
|
100 |
34 |
3400 |
10000 |
-38,3624306 |
33,1775694 |
0,822430563 |
0,67639203 |
|
|
120 |
19 |
2280 |
14400 |
-46,0349167 |
25,5050833 |
-6,50508332 |
42,3161091 |
|
|
120 |
19 |
2280 |
14400 |
-46,0349167 |
25,5050833 |
-6,50508332 |
42,3161091 |
|
|
120 |
19 |
2280 |
14400 |
-46,0349167 |
25,5050833 |
-6,50508332 |
42,3161091 |
|
|
120 |
19 |
2280 |
14400 |
-46,0349167 |
25,5050833 |
-6,50508332 |
42,3161091 |
|
|
120 |
19 |
2280 |
14400 |
-46,0349167 |
25,5050833 |
-6,50508332 |
42,3161091 |
|
|
120 |
19 |
2280 |
14400 |
-46,0349167 |
25,5050833 |
-6,50508332 |
42,3161091 |
|
|
120 |
19 |
2280 |
14400 |
-46,0349167 |
25,5050833 |
-6,50508332 |
42,3161091 |
|
|
150 |
12 |
1800 |
22500 |
-57,5436458 |
13,9963542 |
-1,99635415 |
3,98542991 |
|
|
150 |
12 |
1800 |
22500 |
-57,5436458 |
13,9963542 |
-1,99635415 |
3,98542991 |
|
|
150 |
12 |
1800 |
22500 |
-57,5436458 |
13,9963542 |
-1,99635415 |
3,98542991 |
|
|
150 |
12 |
1800 |
22500 |
-57,5436458 |
13,9963542 |
-1,99635415 |
3,98542991 |
|
|
150 |
12 |
1800 |
22500 |
-57,5436458 |
13,9963542 |
-1,99635415 |
3,98542991 |
|
|
170 |
7 |
1190 |
28900 |
-65,216132 |
6,32386804 |
0,676131958 |
0,45715442 |
|
|
170 |
7 |
1190 |
28900 |
-65,216132 |
6,32386804 |
0,676131958 |
0,45715442 |
|
|
170 |
7 |
1190 |
28900 |
-65,216132 |
6,32386804 |
0,676131958 |
0,45715442 |
|
|
180 |
4 |
720 |
32400 |
-69,052375 |
2,48762499 |
1,512375014 |
2,28727818 |
|
|
180 |
4 |
720 |
32400 |
-69,052375 |
2,48762499 |
1,512375014 |
2,28727818 |
|
|
200 |
2 |
400 |
40000 |
-76,7248611 |
-5,18486113 |
7,184861127 |
51,6222294 |
|
|
200 |
2 |
400 |
40000 |
-76,7248611 |
-5,18486113 |
7,184861127 |
51,6222294 |
|
|
5540 |
1452 |
133810 |
684400 |
|
|
0,278653232 |
540,161666 |
|
|
110,8 |
29,04 |
|
|
|
|
|
|
На основе результатов, приведенных в табл.4, получаем оценки:
a*=
=
-0,38362431
b* = 29,04
d* = b* - a*pср. = 29,04 – (-0,383624)*110,8 = 71,54.
Оценка теоретической функция спроса имеет вид:
D*(p) = - 0,383624*p+ 71,54.
Оценка среднеквадратического отклонения такова:
=
= 3,29
Далее, доверительные границы функции спроса имеют вид:
D*(p)верхн\нижн.
= (-0,383624) + 71,54
1,96*3,29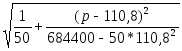
=
=
(-0,383624)p
+71,54
6,45
.
Например, при p =120
D*(120)верхн. = 25,50 +0,9391 = 26,44,
D*(120)нижн. = 25,50 – 0,9391 = 24,56.
Т.о., при цене 120 руб. товар купят 25-26 человек.
Если сравним значения SS в табл. 2 и табл. 4, то заметим разницу. Это связано с тем, что в табл.2 значения были округлены до пятого знака после запятой, а в табл. 4 округления не производились. В данном случае на конечный результат это не повлияло, т.к. данные сами по себе выражены довольно большими числами. Чем меньше значения данных, тем аккуратнее необходимо подходить к процессу округления и сохранять в расчетах достаточное количество значащих цифр.