2.2. Определение основных размеров звеньев:

1. Диаметр поршня:

2. Длина кривошипа :

3. Длина шатуна :

4. Ход поршня :

5. Необходимая частота вращения кривошипного вала компрессора

6. Высота поршня (приближенно равна диаметру поршня):

7. Масса поршня :

8. Масса шатуна (приближенно равна массе поршня):

9. Момент инерции шатуна относительно центра масс :

2.3.Расчет кинематических параметров кривошипно-ползунного механизма

Для определения параметров динамической модели необходим расчет кинематических параметров кривошипно-ползунного механизма. Связь перемещения ползуна (поршня), отсчитанного от ВМТ, с углом поворота кривошипаопределяется методом замкнутого контура.

Расчет организуется по углу поворота кривошипа

Из рассмотрения проекций звеньев на ось Х получим координату поршня:

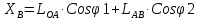
Перемещение поршня от ВМТ

Угол поворота φ2 шатуна находится из рассмотрения проекций на ось У:

Безразмерное отношение перемещения поршня к его ходу имеет вид:

Аналог скорости точки В получается дифференцированием функции положения SH­_φ(φ1):

Передаточное отношение :

U₂₁(ф1) – отношение угловых скоростей шатуна и кривошипа

Аналог скорости точки S (центра масс звена 2) получается из рассмотрения плоского движения шатуна:

Проекция аналога скорости на оси:

На ось Х

На ось У

4. Расчет параметров динамической модели Аппроксимация индикаторной диаграммы

Рабочий процесс любой поршневой машины связан с движением поршня и иллюстрируется индикаторной диаграммой, представляемой в системе координат: давление на поршень – перемещение поршня. При принятых в теоретической механике правилах сил индикаторная диаграмма по отношению к линии атмосферного давления представляет диаграмму сил. В поршневых машинах обычно принимают за положительное направление сил направление от поршня к центру вращения кривошипа, т.е. положительное направление силы соответствует избыточному давлению в цилиндре.

Индикаторная диаграмма приводится таблицей безразмерных изменений давлений и перемещений поршняS/H, где ­– текущее и максимальное абсолютное давления на поршень;– атмосферное давление.

Где SH=S/H – безразмерное отношение перемещения к ходу поршня (S –текущее перемещение поршня от ВМТ (); Н –ход поршня);

PR – безразмерное изменение давления при расширении;

PS – изменение давлении при сжатии ( в долях ).

С помощью сплайновой аппроксимации можно получить зависимость отношения давлений (PR и PS) от отношения перемещения к ходу поршня (SH).

Функция cspline(VX, VY) - возвращает вектор VS вторых производных при приближении в опорных точках к кубическому полиному.

Функция interp(VS, VX, VY, x) – вычисляет промежуточные значения, не заданные массивами PR и PS.

intPR(x) - давление при всасывании в долях от максимального давления;

intPS(x) - давление при сжатии в долях от максимального давления.

Сила действия газов на поршень

Индикаторная диаграмма по отношению к линии атмосферного давления представляет диаграмму действия сил на поршень. При расчете сил давления на поршень используется общепринятое правило знаков сил: за положительное направление сил принято направление от поршня к центру вращения кривошипа, т.е. положительное направление силы соответствует избыточному давлению в цилиндре

Значение силы вычисляется по промежуточным значениям давления в функции перемещения поршня intPR и intPS перестраивается по углу поворота кривошипа заменой переменных.