§ 2.3. Сферические и плоские преломляющие и

отражаю­щие поверхности

Узкий световой конус световых лучей с осью, нормальной к сферической поверхности, называется параксиальным пучком. Непараксиальные пучки не дают стигматических изображений и после преломления перестают быть гомоцентрическими. Область бесконечно малого пространства вблизи оптической оси, внутри которой углы лучей с оптической осью и с нормалями к поверхностями настолько малы, что величины синусов и тангенсов этих углов можно заменить самими углами, называется параксиальной областью.

Рассмотрим преломление лучей на сферической поверхности. LA – падающий, LA’ – преломленный. Из треугольника LAO по теореме о синусах можно записать

. (2.1)

Углы иβ смежные, тогда

; . (2.2)

Из тригонометрии известно: , отсюда

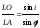. (2.3)

Аналогично из треугольника L'AO можно получить:

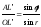. (2.4)

Тогда, перемножив левые и правые части уравнений 2.3 и 2.4, получим: c учетом закона Снеллиуса

. (2.5)

Для параксиальных лучей:

AL SL = - , (2.6)

AL’ SL’ = ;SO = R. (2.7)

Тогда

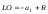, .(2.8)

Подставим 2.6, 2.7, 2.8 в 2.5:

. (2.9)

или

. (2.10)

. (2.11)

Формула 2.10 показывает, что произведение при преломлении сохраняет свою величину, называемую нулевым инвариантом Аббе. Соотношение 2.10 обычно записывают в виде:

. (2.12)

Формула 2.12 позволяет отыскать положение точки если известно положение точкии.

Формулу 2.12 можно применить и к сферическому зеркалу, т.е. к случаю отражения, если положить . Тогда имеем:

. (2.13)

§ 2.4 Кардинальные точки, главные и фокальные

плоскости и фокусные расстояния

Идеально оптической системой называется система, которая дает стигматическое изображение точек пространства предметов с помощью широких гомоцентрических лучей. В идеально оптической системе сохраняется гомоцентричность пучков и изображения геометрически подобны предмету. Рассмотрим идеально оптическую систему:

Задним фокусом оптической системы называется точка, являющаяся изображением бесконечно удаленной точки, лежащей на продолжении оптической оси F’. Это точка, в которой сходится после преобразования параллельные оси лучи В. Передними и задними главными плоскостями называются плоскости в пространстве предметов и изображений, для которых линейное увеличение = +1. Это плоскости, перпендикулярные главной оптической оси и проходящие через отрезки КН и К’Н’. Точка F называется передним фокусом оптической системы. Изображением данной точки является бесконечно удаленная точка в пространстве изображений. Расстояние НF, отсчитываемое от точки Н, называется передним фокусным расстоянием. Расстояние Н’F’, отсчитываемое от точки Н’, называется задним фокусным расстоянием. Плоскости Е и Е’ , перпендикулярны оптической оси и проходящие через точки фокусов F и F’, называются соответственно передней и задней фокальными плоскостями.