
Работа расширения /сжатия в политропном процессе.
![]() ;
;
![]()


5.2.1
физический
маятник -осциллятор,
представляющий собой твёрдое тело,
совершающее колебания в поле каких-либо
сил относительно точки, не являющейся
центром масс этого тела, или неподвижной
оси, перпендикулярной направлению
действия сил и не проходящей через центр
масс этого тела. Момент инерции
относительно оси, проходящей через
точку подвеса:
![]()
---------------------------------------------------------------------------------------------
Если
амплитуда колебаний
![]() мала, то корень в знаменателе эллиптического
интеграла приближенно равен единице.
Такой интеграл легко берется, и получается
хорошо известная формула малых колебаний:
мала, то корень в знаменателе эллиптического
интеграла приближенно равен единице.
Такой интеграл легко берется, и получается
хорошо известная формула малых колебаний:
 .
.
5.2.2 Адиабатический процесс - см. 2.2.2
Поясним понятие
работы применительно к адиабатическому
процессу. В частном случае, когда
работа совершается через изменение
объёма, можно определить её следующим
способом: пусть газ заключён в
цилиндрический сосуд, плотно закрытый
легко скользящим поршнем, если газ будет
расширяться, то он будет перемещать
поршень и при перемещении на отрезок
![]() совершать работу :
совершать работу :
![]()
где F — сила,
с которой газ действует на поршень.
Перепишем уравнение:
![]()
где s — площадь
поршня. Тогда работа будет равна:
![]()
где
![]() —
давление
газа,
—
давление
газа,
![]() —
малое приращение объёма.
—
малое приращение объёма.
5.3.1
Уравнение свободных незатухающих колебаний
|
энергия гармонического осциллятора - кинетическая энергия K системы в функции времени t такова:
и потенциальная
есть:
импульс
- Кинематическое
уравнение линейного гармонического
осциллятора имеет вид :
Продифференцировав
(6) по времени и умножив полученный
результат на массу осциллятора
Фазовая
траектория - кривая в фазовом
пространстве, составленная из точек,
представляющих состояние динамической
системы в последовательные моменты
времени в течение всего времени
эволюции. Динамическая система
задаётся с помощью закона, позволяющего
установить состояние системы в
произвольный (допустимый) момент
времени t>0, если известно её
состояние в начальный момент t =
0. Это означает, что задаётся набор
фазовых переменных x={xi,
i=1, 2, ..., n} и эволюционный
оператор Tt, преобразующий
состояние х0 = х(t =0)в
состояние x(t):
5.3.2
Работа газа при
изобарном расширении:
Работа газа при
изохорном процессе равна нулю:
Работа газа при
изотермическом расширении:
6.1.1 Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных. ------------------------------------------------------------------------------------------------------------
Центром
масс системы материальных точек
называется точка
----------------------------------------------------------------------------------------------------
Вследствие
действия сил на тела системы их импульсы
изменяются.
Бели за малый промежуток времени сила
заметно не меняется, то для каждого
тела системы можно записать изменение
импульса в форме:
Сложим левые и правые части уравнений (6) и покажем, что сумма изменений импульсов отдельных тел равна изменению суммарного импульса всех тел системы, равного
6.1.2 - см. в 3.1.2 6.2.1
Закон
равномерного распределения энергии
по степеням свободы молекул
можно сформулировать следующим
образом: статистически в среднем на
каждую степень свободы молекул
приходится одинаковая энергия.
Поступательное движение молекул
характеризуется средней кинетической
энергией, равной
1-атомная молекула- мат точку J = (x,y,z)- 3 параметра 2-атомная молекула(6 степеней свободы) (x1-x2)^2+(y1-y2)^2+(z1-z2)^2=l 6-1=5 независимых параметров Распределение энергии: <Екин>=l*k*T\2 L=3-одноатомный,l=5-двухатомный,l=6-многоатомный. -------------------------------------------------------------------------------------------
Согласно закону
Джоуля, выведенному эмпирически,
внутренняя энергия идеального
газа не зависит от давления
или объёма. Исходя из этого факта,
можно получить выражение для изменения
внутренней энергии идеального газа.
По определению молярной
теплоёмкости при постоянном
объёме,
6.2.2 Сила в механике - это мера взаимодействия между телами. Все многообразие встречающихся в природе взаимодействий сводится всего лишь к четырем типам. Это гравитационное электромагнитное, ядерное (или сильное) и слабое взаимодействие. В механике Ньютона можно рассматривать только гравитационное и электромагнитное взаимодействия. Сила упругости.
Сила упругости,
действующая на тело со стороны
деформированной (сжатой или растянутой)
пружины, равна по величине
Сила трения.
При скольжении тела действующая
на него сила трения, является функцией
скорости относительного движения.
Сопротивление
среды (мех.) — окружающей
движущееся тело, представляет собой
совокупность сил, противодействующих
движению тела и образуемых ударами
частиц. среды и трением их о поверхность
тела
где Δ есть вес единицы объема жидкости. ----------------------------------------------------------------------------------------------------------------- Динамика мат. точки: она базируется на 3 основных законах, называемых законами Ньютона. Приведем формулировки этих законов: Закон 1. Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного прямолинейного движения, пока оно не понуждается приложенными силами изменить это состояние. Закон 2. Изменение количества движения пропорционально приложенной силе и происходит по направлению прямой, по которой эта сила действует. Закон 3. Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг с другом равны и направлены в противоположные стороны.
6.3.1- см 1.1.2
6.3.2
В
случае, когда одна из систем отсчета
движется относительно другой
поступательно
с постоянной скоростью
------------------------------------------------------------------------------------------------------------------
Из
7.1.1 - см. 2.2.1 7.1.2 - см. 1.2.2 7.2.1
Опыт
показывает, что поверхность жидкости
стремится принять такую форму, чтобы
иметь минимальную площадь. Это явление
связано с воздействием на поверхность
жидкости механических сил, стремящихся
уменьшить площадь этой поверхности.
Указанные силы называются силами
поверхностного натяжения. Величины
Как
следует из этой формулы, равновесию
жидкости на поверхности твердого тела
соответствует вполне определенный
угол
----------------------------------------------------------------------------------------- капиллярный эффект — физическое явление, заключающееся в способности жидкостей изменять уровень в трубках, узких каналах произвольной формы, пористых телах. Поднятие жидкости происходит в случаях смачивания каналов жидкостями, например воды в стеклянных трубках, песке, грунте и т. п. Понижение жидкости происходит в трубках и каналах, не смачиваемых жидкостью, например ртуть в стеклянной трубке Капиллярное давление. Так как силы поверхностного (межфазного) натяжения направлены по касательной к поверхности жидкости, искривление последней ведет к появлению составляющей, направленной внутрь объема жидкости. В результате возникает капиллярное давление, величина которого Dp связана со средним радиусом кривизны поверхности r0 уравнением Лапласа: Dp = p1 - p2 = 2s12/r0, (1) где p1 и p2 - давления в жидкости 1 и соседней фазе 2 (газе или жидкости), s12 - поверхностное (межфазное) натяжение.
7.2.2 Релятивистский закон сложения скоростей -
7.3.1 Интервал - интервал в теории относительности — расстояние между двумя событиями в пространстве-времени. Интервал не меняется при переходе от одной инерциальной системы отсчета к другой, что позволяет чисто формально получить преобразования Лоренца как группу преобразований, сохраняющих интервал. Интервал является одним из фундаментальных физических понятий. Он лежит в основе специальной и общей теорий относительности. Свойство теории сохранять интервал при смене инерциальной системы отсчета называется Лоренц-инвариантностью.
7.3.2
Внутренняя
энергия термодинамической системы
включает в себя энергию микроскопического
движения и взаимодействия частиц
системы, а так же их внутримолекулярную
и внутриядерную энергии. Определяется
в соответствии с первым
началом термодинамики, как
разность между количеством
теплоты, сообщенным системе, и
работой,
совершенной системой над внешними
телами:
----------------------------------------------------------------------------------------------------
Количество теплоты, сообщаемой
телу, идёт на увеличение внутренней
энергии и на совершение телом работы:
Правило
знаков:
Важно отметить, что теплота Q и работа А зависят от того, каким образом совершен переход из состояния 1 в состояние 2 (изохорически, адиабатически и т.д.), а внутренняя энергия U не зависит. При этом нельзя сказать, что система обладает определенным для данного состояния значением теплоты и работы. ---------------------------------------------------------------------------------------------- Первое начало термодинамики – dQ=dA+dU — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем. dQ – зависит от процесса перехода из 1-го состояния в другие; dA- зависит от процесса ; dU- не зависит от процесса.
8.1.1 наиболее важным и часто встречающимся типом гармонических волн являются плоские гармонические волны.
Стоячая
плоская волна:
--------------------------------------------------------------------------------------------
Длина́
волны́ —
расстояние
между двумя ближайшими друг к другу
точками, колеблющимися в одинаковых
фазах,
обычно длина волны обозначается
греческой буквой
----------------------------------------------------------------------------------------------------
Фа́зовая
ско́рость —
скорость перемещения точки, обладающей
постоянной фазой
колебательного движения, в пространстве
вдоль заданного направления. Обычно
рассматривают направление, совпадающее
с направлением волнового
вектора,
и фазовой называют скорость, измеренную
именно в этом направлении, если
противное не указано явно. Основная
формула, определяющая фазовую скорость
(монохроматической) волны в одномерном
пространстве:
Любая волна,
описываемая волновым
уравнением:
-------------------------------------------------------------------------------------------------------- Волновой вектор — вектор, направление которого перпендикулярно фазовому фронту бегущей волны, а абсолютное значение равно волновому числу.
Волновой вектор
обычно обозначается латинской буквой
---------------------------------------------------------------------------------------------------------
СФЕРИЧЕСКАЯ
ВОЛНА - волна, радиально расходящаяся
от некоторой точки (источника) или
сходящаяся к ней (к стоку) и имеющая
сферические волновые фронты (поверхности
равных фаз). Простейшим примером
является сферически симметричная
скалярная волна вида:
8.1.2 Неравенство Клаузиуса (1854): Количество теплоты, полученное системой при любом круговом процессе, делённое на абсолютную температуру, при которой оно было получено (приведённое количество теплоты), неположительно.
Термодинамическая
энтропия
S,
часто просто именуемая энтропия,
в химии
и термодинамике
является функцией
состояния
термодинамической
системы
------------------------------------- см 1.3.2
8.2.1
8.2.2 - см. 2.1.2
8.3.1
Вынужденные
колебания
-колебания,
происходящие под воздействием внешних
сил, меняющихся во времени.Автоколебания
отличаются от вынужденных колебаний
тем, что последние вызваны периодическим
внешним воздействием и происходят с
частотой этого воздействия, в то время
как возникновение автоколебаний и их
частота определяются внутренними
свойствами самой автоколебательной
системы.Наиболее простой и содержательный
пример вынужденных колебаний можно
получить из рассмотрения гармонического
осциллятора и вынуждающей силы, которая
изменяется по закону:
Механический резонанс - явление возрастания амплитуды вынужденных колебаний в какой-либо колебательной системе при приближении частоты периодического внешнего воздействия к одной из частот собственных колебаний системы. Характер Р существенно зависит от свойств колебательной системы. Простейший случай Р наступает при периодическом воздействии на линейную систему, т.е. систему с параметрами, не зависящими от состояния самой системы. Примером линейной системы с одной степенью свободы является масса m, подвешенная на пружине и находящаяся под действием гармонической силы F = F0 cos(wt)
8.3.2 Из формулировки второго начала термодинамики по Кельвину следует, что вечный двигатель второго рода — периодически действующий двигатель, совершающий работу за счет охлаждения одного источника теплоты, — невозможен Принцип действия теплового двигателя : от термостата* с более высокой температурой Т1, называемого нагревателем, за цикл отнимается количество теплоты Q1, а термостату с более низкой температурой Т2, называемому холодильником, за цикл передается количество теплоты Q2, при этом совершается работа А = Q1 – Q2. -------------------------------------------------- См. 4.2.2
9.1.1 Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.
Для абсолютно
твёрдого тела полную кинетическую
энергию можно записать в виде суммы
кинетической энергии поступательного
и вращательного движения:
9.1.2 Фазовое пространство – воображаемое математическое пространство, число измерений которого равно количеству переменных, определяющих состояние данной системы. (Дать по запись). Если система состоит из N частиц, то ее состояние будет определяться 6N переменными. Такую же размерность будет иметь и фазовое пространство этой системы. Из-за непрерывного движения и столкновения частиц микросостояние системы все время меняется.Фазовый объем системы из N частиц, суммарная кинетическая энергия которых близка к какому-либо значению Е, определяется выражением: Г=CVNE3N/2 где С — некоторый коэффициент пропорциональности. -----------------------------------------------------------------
Полученное
распределение, характеризующее
вероятность того, что молекула имеет
данный импульс и находится в данном
элементе объема, называется распределением
Максвелла-Больцмана.
9.2.1 Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем. И см. 3.3.2
9.2.2 Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.
Для идеального
газа, имеющего постоянную
температуру
где
--------------------------------------------------------------------------------------------------- Распределение Больцмана — распределение вероятностей различных энергетических состояний идеальной термодинамической системы (идеальный газ атомов или молекул) в условиях термодинамического равновесия.
9.3.1 Момент силы — аксиальный вектор. Он направлен вдоль оси вращения. Направление вектора момента силы определяется правилом буравчика, а величина его равна M. M = F*r
.
.
|
|
|

 это
дифференциальное уравнение
свободных гармонических незатухающих
колебаний. Решение уравнения (2)
будем искать в виде:
это
дифференциальное уравнение
свободных гармонических незатухающих
колебаний. Решение уравнения (2)
будем искать в виде:
 .
. (6)
(6) ---------------------------------------------------------------------
---------------------------------------------------------------------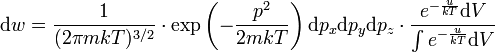

 --------------------------------------------------------
--------------------------------------------------------