Обобщенный закон Гука

Между компонентами тензора деформаций (2.7) и компонентами тензора напряжений (1.5) существует связь, которая, в принципе, может быть установлена только экспериментальным путем. Опыт показывает, что для большинства материалов при умеренных нагрузках связь между напряжениями и деформациями может быть принята линейной. Это обнаруживается при испытании стандартных образцов в условиях одноосного растяжения. Вплоть до значения напряжения называемогопределом пропорциональности, справедлив закон Р. Гука (1676 г.): напряжения прямо пропорциональны деформации удлинения:

(2.9)

В законе Гука коэффициент пропорциональности называетсямодулем упругости. Он характеризует жесткость материала и в приведенных ниже случаях приблизительно равен: сталь — МПа; алюминиевые сплавы — МПа; древесина вдоль волокон (сосна) — МПа.

Закон Гука можно записать в виде

Воспользуемся этим соотношением и принципом независимости действия сил для того, чтобы получить закон Гука для трехосного напряженного состояния. Обратим внимание на то, что с точностью до малых высшего порядка нормальные напряжения не вызывают сдвигов, а касательные напряжения не вызывают удлинений ребер элемента. Рассмотрим малый элемент, показанный на рис. 2.3. Пусть на элемент действует только напряжение атогда деформации в направлении координатных осей будут равны:

При и

При и

Деформация удлинения в направлении оси при совместном действии всех напряжений будет равна

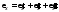
Аналогичным образом определятся деформации в направлении других координатных осей. Подставляя выражения для после очевидных преобразований получим три уравнения:

(2.10)

Добавим к этим уравнениям еще три соотношения, вытекающие из закона Гука при чистом сдвиге (двухосное напряженное состояние, при котором на гранях элемента возникают только касательные напряжения):

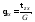(2.11)

Три упругие постоянные (модуль упругости модуль сдвигаи коэффициент Пуассона) не являются независимыми. Они связаны между собой соотношением

(2.12)

Шесть полученных уравнений, связывающих между собой компоненты тензоров напряжений и деформаций, составляют так называемый обобщенный закон Гука.

Три дифференциальных уравнения равновесия, шесть соотношений Коши и шесть уравнений обобщенного закона Гука составляют систему уравнений теории упругости, в которой неизвестными будут шесть независимых компонент тензора напряжений, шесть независимых компонент тензора деформаций и три компоненты вектора перемещения.

Теории перехода в пластическое состояние.

Рассмотрим следующие теории (гипотезы) перехода в пластическое состояние.

Теория наибольших касательных напряжений.

Согласно этой теории считается, что критерием перехода в пластическое состояние является величина наибольшего касательного напряжения.

Так как оба состояния равноопасны, а критерием перехода в предельное состояние является величина наибольшего касательного напряжения, то естественно считать, что наибольшие касательные напряжения в обоих случаях можно считать равными

Теория энергии формоизменения.

Потенциальная энергия деформации может быть представлена в виде суммы двух слагаемых: потенциальной энергии изменения объема и потенциальной энергии формоизменения. Последняя величина может служить критерием перехода в пластическое состояние.

Для сложного напряженного состояния потенциальная энергия формоизменения выражается (если отнести энергию к единице объема):

Для одноосного напряженного состояния

Т.к. оба напряженных состояния равноопасны, то обе величины можно приравнять и в результате:

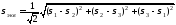
Теория Мора

В отличие от предыдущих теорий (гипотез), являющихся критериальными гипотезами, теория Мора отправляется от опыта и носит феноменологический характер. Допустим, что мы располагаем возможностью испытывать образцы в условиях сложного напряженного состояния, задавая всевозможные напряженные состояния с пропорциональным изменением компонента напряженного состояния.

Доведя напряженное состояние до предельного, можно построить большой круг Мора (на напряжениях). Поступая таким образом, в случае других напряженных состояний, можно построить семейство больших кругов Мора для различных предельных состояний. Огибающая этих кругов – предельная огибающая, является объективной характеристикой материала ( как, например, диаграмма растяжения) и она позволяет для конкретного напряженного состояния вычислить коэффициент запаса.

Однако в действительности у нас имеется возможность произвести испытания только на растяжение и сжатие и построить два соответствующих круга Мора.

Предельная огибающая аппроксимируется прямой, касающейся двух окружностей, указанных круговых диаграмм.

Исходя из такого представления предельной огибающей, найдем выражение для .

Пусть компоненты некоторого напряженного состояния, которое необходимо оценить, заданы и известны главные напряжения . В предельном состоянии главные напряжения будут равны

Круг Мора, построенный на этих напряжениях, будет касаться предельной огибающей в точке А.

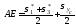
Подставляя выражения для отрезков в пропорцию (*),

Вспоминая, что , приходим к выводу что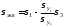. Обозначив , имеем

формулу для эквивалентных напряжений

Несмотря на то, что для материала пластичного одинаково работающего на растяжение и сжатие формула теории Мора совпадает с формулой теории наибольших касательных напряжений. Не следует говорить, что теория наибольших касательных напряжений является частным случаем теории Мора. Исходные посылки этих теорий различны и если бы была возможность уточнить предельную огибающую, то выражение для эквивалентных напряжений по теории Мора была бы другой.