Напряжения при косом изгибе.

В силу высказанных ранее причин мы не будем интересоваться касательными напряжениями, возникающими в данном случае. Рассмотрим сечение балки. Оси и- главные центральные оси сечения. Плоскость действия изгибающего момента в сечении не совпадает с плоскостями, в которых лежат главные оси.

След плоскости изгибающего момента на плоскости сечения будем называть силовой линией. Угол между силовой линией и положительным направление оси обозначим. Пусть точкас координатами- произвольная точка сечения. Наша задача – найти напряжение в данной точке, т.е. установить закон изменения напряжений по сечению:.

Разложим изгибающий момент на два моментаи- изгибающие относительно главных центральных осей.

Используя принцип независимости действия сил, определим напряжение, как сумму напряжений от составляющих моментов

и

Как видим, косой изгиб представляет собой комбинацию двух прямых изгибов относительно главных осей. Если использовать выражения для 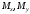, то полученной формуле можно придать другой вид:

Напряжения в сечении распределяются по линейному закону (если откладывать в каждой точке вектор напряжений, то множество концов векторов будет плоскостью). Нас прежде всего интересует величина наибольшего по модулю напряжения в сечении.

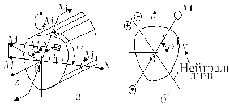
Поступим следующим образом. Вначале найдем нейтральную линию в сечении, т.е. такую линию, в точках которой напряжения равны нулю. Для этого нужно приравнять выражение (1) или (1а) нулю:

Уравнение (2) однородно, следовательно нейтральная ось проходит через центр тяжести. Можно показать, что нейтральная линия не перпендикулярна к силовой.

На самом деле. Угловой коэффициент нейтральной линии: , а силовой линии. При,

т.е. условие перпендикулярности не выполняется. (Что будет при ?) Нанеся на чертеж сечения, нейтральную линию мы можем убедиться что она отклоняется в сторону более “слабой” оси, т.е. оси с меньшим моментом инерции.

В силу характера распределения напряжений, наибольшие по модулю напряжения возникают в точке наиболее удаленной от нейтральной линии. Пусть такой будет точка с координатами(рис.6). Подставив в уравнение для напряжений координаты этой точки, получим выражение для максимальных по модулю напряжений

Внецентренное растяжение и сжатие.

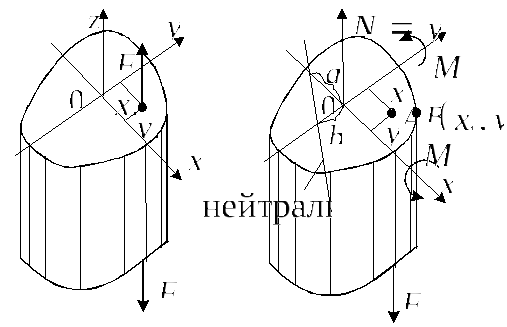
Если в поперечном сечении помимо изгибающих моментов (в двух плоскостях) возникают еще и нормальные силы, то данный случай является комбинацией косого изгиба и обыкновенного (центрального) растяжения или сжатия. Напряжение можно определить по формуле:

Подобная ситуация возникает в случае внецентренного растяжения или сжатия, когда равнодействующая сил, действующих на стержень параллельна оси, но совпадает с ней.

Оси и- главные центральные оси сечения.

- координаты точки приложения (следа) силы F.

Внутренние силовые факторы в сечении:

Подставляя в (5) получаем закон распределения нормальных напряжений при растяжении (сжатии)

Здесь учтено, что (радиусы инерции сечения)

и

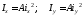
В дальнейшем ход рассуждения такой же как и при косом изгибе. Уравнение нейтральной линии получим, приравняв выражение (6) нулю.

Уравнение не однородно, в отличии от случая косого изгиба, нейтральная ось не проходит через центр тяжести.

Придадим уравнению другую форму:

, где - отрезки,

отсекаемые нейтральной линией на координатных осях.

Наибольшие по модулю напряжения возникают в точке, наиболее удаленной от нейтральной оси. Пусть такой точкой будет точка

с координатами . Тогда:

Если сечение прямоугольное или вписывается в прямоугольник, то .