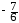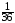Дисперсия случайной величины.

Дисперсия D случайной величины  определяется формулой

D = M( – M)²

Дисперсия случайной величины — это математическое ожидание квадрата отклонения случайной величины от её математического ожидания.

Рассмотрим случайную величину  с законом распределения

	1	2	3
Р

Вычислим её математическое ожидание.

M = 1 + 2 + 3 = 

Составим закон распределения случайной величины  – M

– M
Р

а затем закон распределения случайной величины ( – M)²

(– M)2
Р

Теперь можно рассчитать величину D :

D =  +  +  = 

Используя определение дисперсии, для дискретной случайной величины формулу вычисления дисперсии можно представить в таком виде: D = 

Можно вывести ещё одну формулу для вычисления дисперсии:

D = 

=   M² – M²

Таким образом, дисперсия случайной величины равна разности мате­матического ожидания квадрата случайной величины и квадрата её математи­ческого ожидания.

ПРИМЕР. Найти дисперсию случайной величины, заданной законом распределения

	1	0
Р	p	q

Выше было показано, что M = р. Легко видеть, что M² = р. Таким образом, получается, что D = р – р² = pq.

Дисперсия характеризует степень рассеяния значений случайной величины относительно её математического ожидания. Если все значения случайной величины тесно сконцентрированы около её математического ожидания и большие отклонения от математического ожидания маловероятны, то такая случайная величина имеет малую дисперсию. Если значения случайной величины рассеяны и велика вероятность больших отклонений от математического ожидания, то такая случайная величина имеет большую дисперсию.

Свойства дисперсии.

1. Если k – число, то D(k) = k² D.

Доказательство.

D(k) = M(k – M(k))² = M(k – k M)² = M(k² ( – M)²) = k²M( – M)² = k² D

2. Для попарно независимых случайных величин ₁, ₂,, _n справедливо равенство

Это свойство оставим без доказательства. Рекомендуем читателю рассмотреть следующий пример.

Пусть  и  – независимые случайные величины с заданными законами распределения:

	0	1			1	2
Р	0,25	0,75		Р	0,7	0,7

Показать, что D( + ) = D + D.

Лекция 6. Биномиальный закон распределения.

Пусть заданы числа n  N и p (0 p  1). Тогда каждому целому числу из промежутка [0; n] можно поставить в соответствие вероятность, рассчитанную по формуле Бернулли. Получим закон распределения случайной величины (назовём её )

	0		k		n
Р					

Будем говорить, что случайная величина  распределена по закону Бернулли. Такой случайной величиной является частота появления события А в n повторных независимых испытаниях, если в каждом испытании событие А происходит с вероятностью p.

Рассмотрим отдельное i-е испытание. Пространство элементарных исходов для него имеет вид

Определим на этом пространстве случайную величину _i следующим образом:

_i = 1, если происходит событие А;

_i = 0, если происходит событие

Закон распределения случайной величины _i рассматривался в предыдущем параграфе.

i	1	0
Р	p	q = 1–p

M = р; D = рq

Для i = 1,2,,n получаем систему из n независимых случайных величин _i, имеющих одинаковые законы распределения. Если теперь сравнить законы распределения двух случайных величин  и , то можно сделать очевидный вывод: = . Отсюда следует, что для случайной величины, имеющей закон распределения Бернулли, математическое ожидание и дисперсия определяются формулами M = M= ==np; D = D= ==npq

Найдём оценку величины р — вероятности успеха в одном испытании некоторого биномиального эксперимента. Для этого проведём n испытаний и подсчитаем х – число успехов. Оценку р^* неизвестной величины р определим формулой р^* = .

ПРИМЕР. Из 20 отобранных для контроля образцов продукции 4 оказались нестандартными. Оценим вероятность того, что случайно выбранный экземпляр продукции не отвечает стандарту отношением р^* = 4/20 = 0,2.

Так как х случайная величина, р^* – тоже случайная величина. Значения р^* могут меняться от одного эксперимента к другому (в рассматриваемом случае экспериментом является случайный отбор и контроль 20-ти экземпляров продукции). Каково математическое ожидание р^*? Поскольку х есть случайная величина, обозначающая число успехов в n испытаниях по схеме Бернулли, Мx = np. Для математического ожидания случайной величины р* по определению получаем: Mp* = M, но n здесь является константой, поэтому по свойству математического ожидания

Mp* = 

Таким образом, “в среднем” получается истинное значение р, чего и следовало ожидать. Это свойство оценки р* величины р имеет название: р* является несмещённой оценкой для р. Отсутствие систематического отклонения от величины оцениваемого параметра р подтверждает целесообразность использования величины р* в качестве оценки. Вопрос о точности оценки пока оставляем открытым.