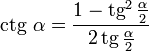Основные тригонометрические формулы

Основные тригонометрические формулы

Формула	Допустимые значения аргумента	Номер
		(1)
		(2)
		(3)

Формула (1) является следствием теоремы Пифагора. Формулы (2) и (3) получаются из формулы (1) делением на  и  соответственно.

[править]Формулы сложения аргументов

Формулы сложения аргументов
	(4)
	(5)
	(6)
	(7)

Формула (6) получается при делении (4) на (5). А формула (7) — при делении (5) на (4)

Вывод формул  [показать]

[править]Формулы двойного угла

Формулы двойного угла выводятся из формул (4), (5) , (6) и (7), если принять, что угол β равен углу α:

Формулы двойного угла
	(23)
	(24)
	(25)

Примечания  [показать]

[править]Формулы тройного угла

Формулы тройного угла

Примечания  [показать]

[править]Формулы понижения степени

Формулы понижения степени выводятся из формул (24):

Синус		Косинус		Произведение
	(26)		(27)

[править]Формулы преобразования произведений функций

Формулы преобразования произведений функций
	(28)
	(29)
	(30)

Вывод формул преобразования произведений функций  [показать]

[править]Формулы преобразования суммы функций

Формулы преобразования суммы функций
	(31)
	(32)
	(33)
	(34)
	(35)

Вывод формул преобразования суммы функций  [показать]

[править]Решение простых тригонометрических уравнений

• 

Если  — вещественных решений нет.

Если  — решением является число вида 

• .

Если  — решений нет.

Если  — решением является число вида 

• 

Решением является число вида 

• 

Решением является число вида 

[править]Универсальная тригонометрическая подстановка

Основная статья: Универсальная тригонометрическая подстановка

Тождества имеют смысл, только когда существуют обе части (то есть при ).

[править]Вспомогательный аргумент (формулы сложения гармонических колебаний)

[править]Полезные тождества

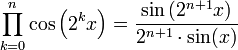
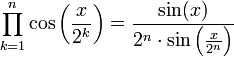
[править]Представление тригонометрических функций в комплексной форме

Основная статья: Формула Эйлера

Формула Эйлера утверждает, что для любого вещественного числа  выполнено следующее равенство:

где  — основание натурального логарифма,

 — мнимая единица.

При помощи формулы Эйлера можно определить функции  и  следующим образом:

,

.

Откуда: