
3.3. Метод приведения масс и моментов инерции
Рассмотрим метод приведения масс на примере МА с кривошипно – ползунным механизмом (см. рис.2.2). Приведение, т.е. замена реальных масс механизма на условные приведенные осуществляется из условия равенства кинетических энергий реальных звеньев и энергии звена приведения, наделяемого условным суммарным приведенным моментом инерции:
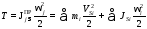
где: mi, JSi - масса и момент инерции относительно центра масс Si i-го звена; VSi – линейная скорость центра масс звена i; wj, w i – угловые скорости звеньев (индекс j соответствует номеру звена, выбранного за звено приведения).
Суммарный приведенный к звену jсуммарный момент инерции
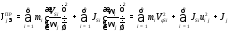 ,
,
является квадратичной формой кинематических передаточных функций. Выбирая вал 1 в качестве звена приведения, угловая координата j1 которого будет обобщенной координатой j, получим выражение суммарного приведенного момента инерции
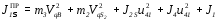 ,
,
где J1 - момент инерции звена 1 относительного центра вращения.
Если в качестве звена приведения выбрать выходное МА (рис.3.6), то выражение для суммарного приведенного момента инерции примет вид
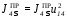 .
.
Анализ приведенных моментов инерции позволяет разделить их на две группы:
1.
Постоянную составляющую моментов
инерции
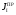 –
так называемую первую группу звеньев,
играющую в некоторых случаях положительную
роль снижения колебаний скорости звена
приведения на установившемся режиме.
–
так называемую первую группу звеньев,
играющую в некоторых случаях положительную
роль снижения колебаний скорости звена
приведения на установившемся режиме.
2.
Периодическую переменную составляющую
приведенного суммарного момента инерции
 ,
так называемой второй группы звеньев,
являющуюся внутренним источником
колебаний.Вторая
группа звеньев может быть значительно
снижена (уравновешена). Например, в
многоцилиндровом ДВС выбор формы
коленчатого вала позволяет снизить
неравномерность вращения и произвести
уравновешивание машины наиболее
эффективным способом.
,
так называемой второй группы звеньев,
являющуюся внутренним источником
колебаний.Вторая
группа звеньев может быть значительно
снижена (уравновешена). Например, в
многоцилиндровом ДВС выбор формы
коленчатого вала позволяет снизить
неравномерность вращения и произвести
уравновешивание машины наиболее
эффективным способом.
Таким образом, при определении приведенных моментов сил и моментов инерции не требуется знания законов движения звеньев, для расчёта необходимы лишь кинематические передаточные функции. Поскольку значения их зависят от обобщенной координаты, то параметры динамической модели в общем случае не постоянны, они являются функцией обобщенной координаты звена приведения jj и зависят от его выбора. Поэтому в качестве звена приведения целесообразно принимать вращающееся звено. которое не совершает остановки, кинематические передаточные функции при таком выборе ни при каких положениях механизма не обращаются в бесконечность.
Рассмотрение общих свойств динамической модели механизма с числом степеней свободы w = 1 и жесткими звеньями показывает, что сфера применения одномассовой динамической модели включает определение закона движения, рассмотрение энергетических процессов в машине и оптимизация на этой основе параметров МА по динамическим критериям и критериям экономичности расхода энергии.
3.4. Расчёт закона движения машины по математической модели
Закон
движения выбранного звена может быть
найден по приведенным к нему параметрам
динамической модели МΣ(φ)
и JΣ
(φ).
Применим теорему об изменении кинетической
энергии и, упустив для упрощения записи
номер звена в обозначении угла поворота
j,
угловой скорости
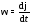 и ускорения
и ускорения
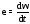 ,получим
,получим
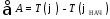 ,
,
где
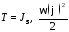 и
и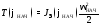 -
текущее и начальное значение кинетической
энергии; jнач,
wнач
, Jå(jнач)
– начальные значения угловой координаты,
скорости и суммарного приведенного
момента инерции.
-
текущее и начальное значение кинетической
энергии; jнач,
wнач
, Jå(jнач)
– начальные значения угловой координаты,
скорости и суммарного приведенного
момента инерции.
Сумму работ можно представить в виде интеграла с переменным верхним пределом φ от суммарного приведенного момента МΣ(φ) по углу поворота, поэтому
 .
.
Закон движения w(j) звена приведения представляет решение предыдущего уравнения суммарной работы в функции обобщенной координаты j
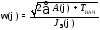 .
.
Таким образом закон движения звена приведения определяется изменением приведенного момента сил и приведенного момента инерции, являющихся при расчёте функцией координаты звена приведения.
Продифференцировав выражение суммы работ по координате j, получим уравнение движения в дифференциальальной форме
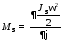 .
.
Учитывая, что начальное значение кинетической энергии машиныTнач величина постоянная, получим дифференцированием
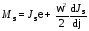 ,
,
угловое ускорение звена приведения
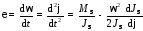 .
.
Каким
бы сложным не был
МА
с одной степенью свободы, выполнив
приведение сил и масс, его можно
представить как одно звено с переменным
моментом инерции, в общем случае зависящим
от обобщенной координаты j.
Поэтому алгоритм расчета динамической
модели часто строится в функции j,
принимаемой за независимую переменную.
Как правило, возникает необходимость
связать расчетные значения координаты
j
со временем. Для этого запишем известное
соотношение угловой скорости
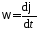 ,
откуда выразим бесконечно малый интервал
времени
,
откуда выразим бесконечно малый интервал
времени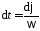 .
Проинтегрируем его и получим время
.
Проинтегрируем его и получим время
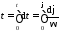 .
.
Таким
образом, определение времени движения
связано с интегрированием обратной
функции закона движения
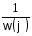 .
.
В многоцилиндровых ДВС расчёты производятся, принимая МΣ и JΣ независящими от угловой координаты вала j, но момент на валу ДВС явно зависит от скорости (рис. 1.8). Для определения закона движения необходимо взять выражение его в дифференциальной форме
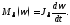
Разделив
переменные
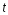 и
и
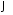 и
проинтегрировав его при начальных
условиях
и
проинтегрировав его при начальных
условиях
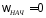 ,
получим
выражения для определения времени
движения при зависимости сил от скорости
,
получим
выражения для определения времени
движения при зависимости сил от скорости
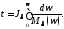
Для анализа возможных режимов движения машин рассмотрим полученное уравнение движения, отметив, что значения приведенных моментов сил и моментов инерции JΣ (φ) зависят от обобщенной координаты j или времени. Можно сделать вывод, что процессы работы МА делятся на две группы (рис. 3.1):
Установившийся режим движения с циклом изменения скорости начального звена, которая или постоянна (стационарный режим) или совершает периодические колебания около среднего значения wср (рис. 3.1 а). Суммарная работа движущих сил и сил сопротивления за цикл равна нулю. Колебания происходят за счет периодических изменений работ сил и кинематических передаточных функций механизма. При работе машины скорости её движения могут периодически принимать одни и те же значения, связанные с изменением сил и совершаемых ими работ. Если период такого цикла движения не меняется как показано на рисунке 3.1.а, то такой режим принято называть режимом установившегося движения. Установившееся движение характеризуется амплитудой колебаний скорости и периодом колебаний jцикла, который определяется частотой действия внешних возмущений или цикловым углом работы механизма;
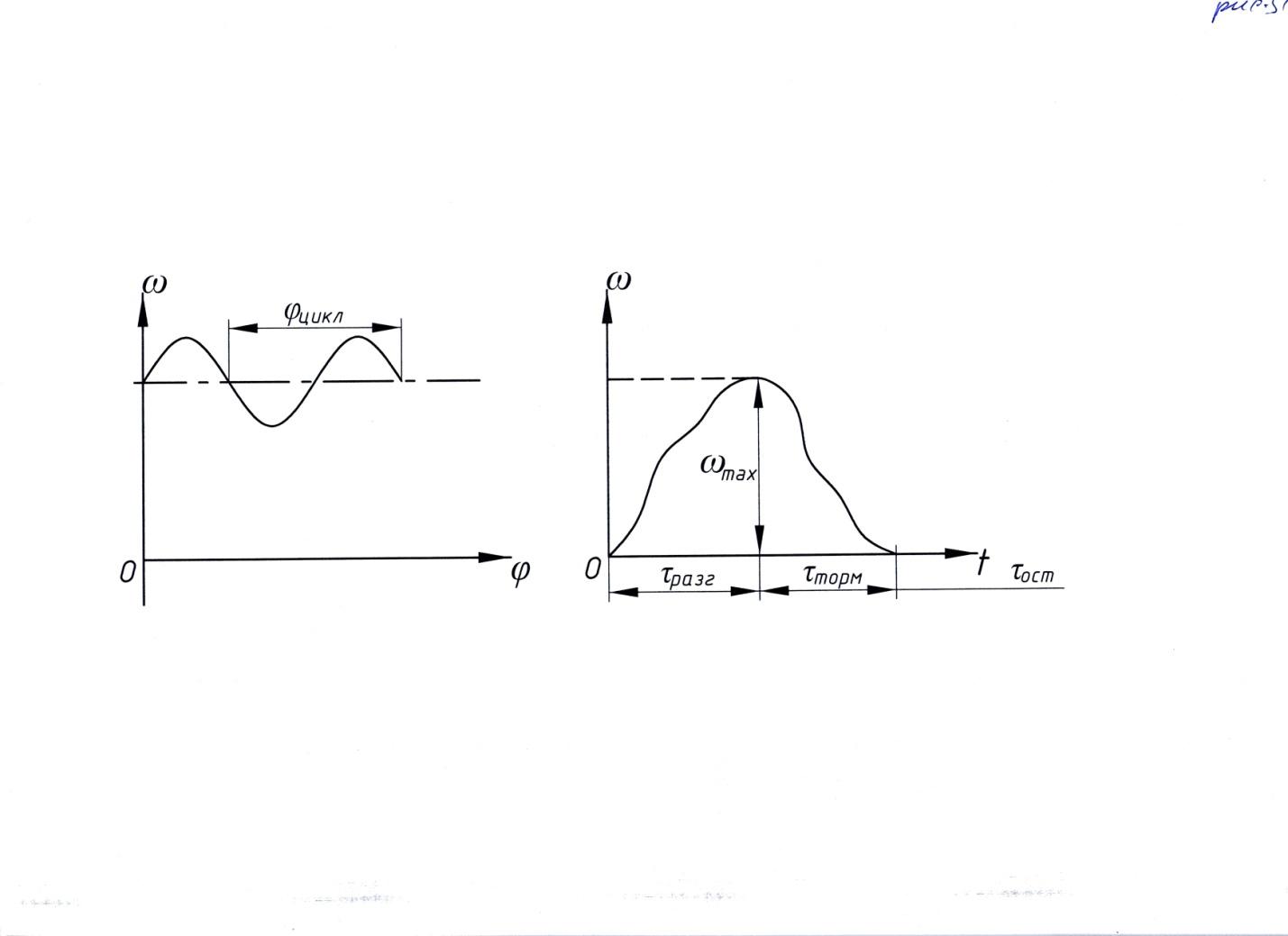
Неустановившиеся режимы разгона и торможения являются переходными (неравновесными процессами) между установившимися режимами:
Разгон – режим неустановившегося движения с возрастанием скорости звена за счет превышения работы движущих сил над работой сил сопротивления. Время разгона машинного агрегата до заданной скорости tразг является важнейшей динамической характеристикой, характеризующей быстродействие и производительность МА;
Торможение (останов) – переходный режим, на котором работа сил сопротивления превышают работу движущих сил, за счет чего происходит снижение кинетической энергии и скорости МА. Время торможения tторм часто бывает не менее важной характеристикой, чем время разгона;
У некоторых машин установившееся движение может отсутствовать, а разгон и торможение могут следовать непосредственно друг за другом. В таком “комбинированном цикле непериодического неустановившегося движения” (рис. 3.1 б), характеризующегося остановками звена приведения на неопределённое время tост начальные и конечные параметры движения являются одинаковыми «нулевыми», что наделяет такой цикл «разгон – торможение » свойствами как установившегося так и неустановившегося движения.
рис. 3.1.
Комбинация двух неустановившихся режимов: разгона @073 и торможения B>@< без установившегося режима между ними показана на рисунке 1.1 б. Эта комбинация обладает одинаковыми начальными и конечными значения скоростей, поэтому изменение кинетической энергии равно нулю подобным циклу установившегося движения. Однако эта комбинация может повторяться через неопределённое время остановки >AB, что не позволяет выделить общий период цикла с остановкой, хотя можно выделить период движения
