
- •Карондеев а.М. Козлов а.А. Силков а.А. Сложение по модулю в блочном шифровании
- •Введение
- •Линейные статистические аналоги сложения по модулю
- •Особенности использования линейных статистических аналогов при анализе блочных шифров
- •Нелинейные статистические аналоги сложения по модулю
- •Криптоанализ на основе нелинейных статистических аналогов
- •Описание метода криптоанализа
- •Используемые аппроксимации
- •Оценка сложности
- •Использованная литература
-
Криптоанализ на основе нелинейных статистических аналогов
-
Описание метода криптоанализа
Общая
идея – получить соотношение связывающие
некоторые биты открытого текста,
шифртекста и ключа, которое выполняется
с преобладанием существенно больше
нуля. Соотношения (7) и (8) не являются
линейными, поэтому и итоговое соотношение
будет нелинейным. Покажем, что это не
мешает использовать лемму о накапливании.
Действительно как было показано в леммах
1, 2 для фиксированного ключа, наибольшее
преобладание достигается при фиксированном
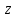 ,
при проведении анализа будем перебирать
всевозможные
,
при проведении анализа будем перебирать
всевозможные
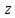 и на одном из них итоговое соотношение
будет выполнятся с наибольшим
преобладанием. При подстановке этого
и на одном из них итоговое соотношение
будет выполнятся с наибольшим
преобладанием. При подстановке этого
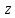 ,
итоговое соотношение сведется к линейному
для которого применима лемма о
накапливании. По сути, перебирая
всевозможные
,
итоговое соотношение сведется к линейному
для которого применима лемма о
накапливании. По сути, перебирая
всевозможные
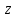 ,
мы выбираем из нескольких линейных
соотношений то, которое выполняется с
наибольшим преобладанием. С
учетом вышесказанного произведем
криптоанализ блочного шифра описанного
в 3 части, более детальная схема которого
изображена на рисунке 9.
,
мы выбираем из нескольких линейных
соотношений то, которое выполняется с
наибольшим преобладанием. С
учетом вышесказанного произведем
криптоанализ блочного шифра описанного
в 3 части, более детальная схема которого
изображена на рисунке 9.
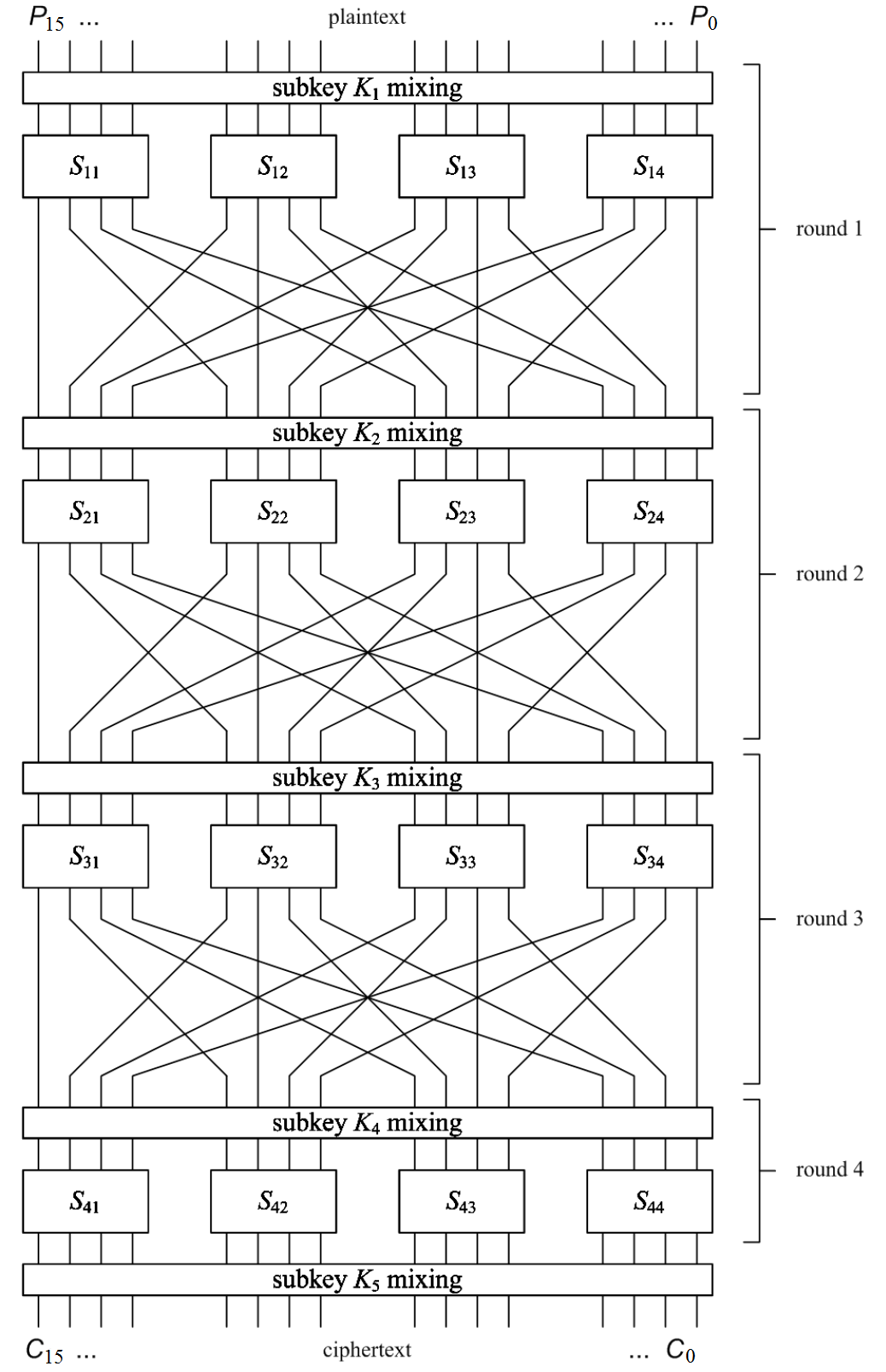
Рисунок 4. Схема шифрования
-
Используемые аппроксимации
Для проведения анализа будем использовать следующие соотношения:
-
Нелинейные соотношения для блока сложения по модулю 2n:
-
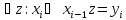 выполняется
с преобладанием больше
выполняется
с преобладанием больше
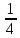
-
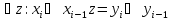 выполняется
с преобладанием больше
выполняется
с преобладанием больше
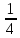
-
Корреляционную матрицу S-блока
Корреляционная матрица рассматриваемого S-блока приведена на рисунке 3 (выделенные ячейки соответствуют аппроксимациям, используемым в активных S-блоках):
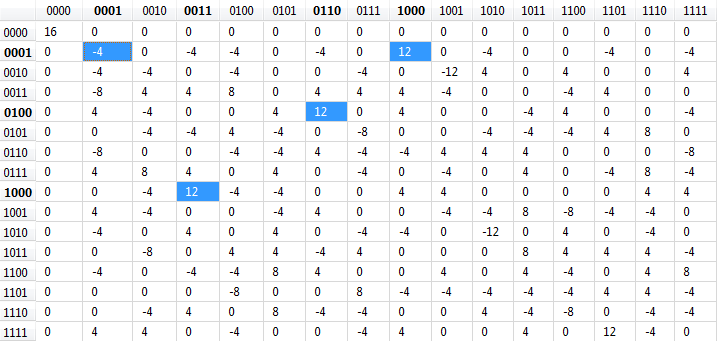
Рисунок 5. Корреляционная матрица S-блока
Активными назовем S-блоки, участвующие в линейном соотношении. Активные блоки выбирались так, чтобы максимизировать преобладание конечной линейной аппроксимации.
На рисунке 9 приведен путь используемой аппроксимации:
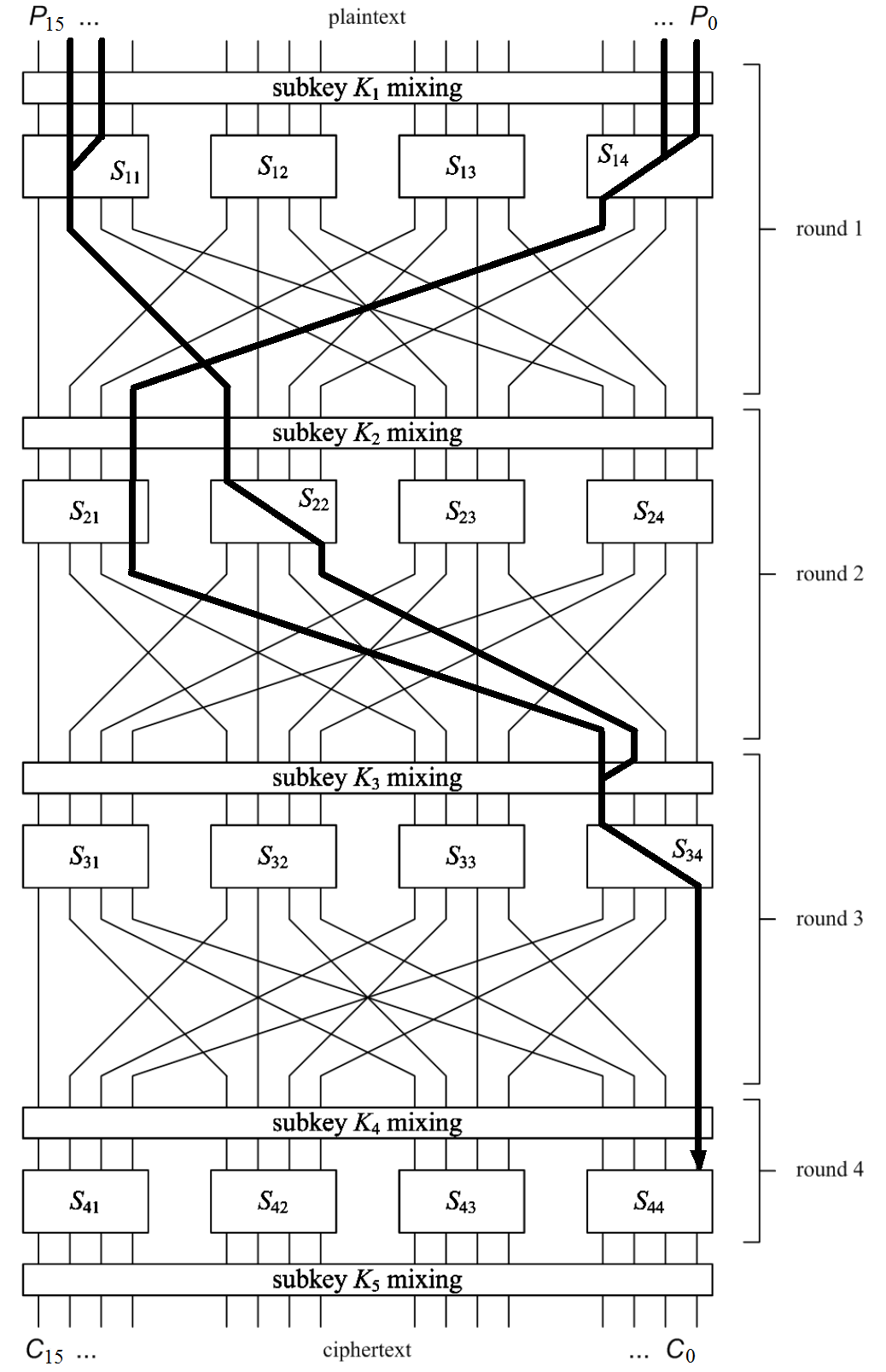
Рисунок 9. Схема нелинейной аппроксимации
Согласно приведенной схеме активными S-блоками являются:
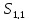 ,
,
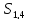 ,
,
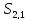 ,
,
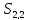 ,
,
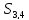
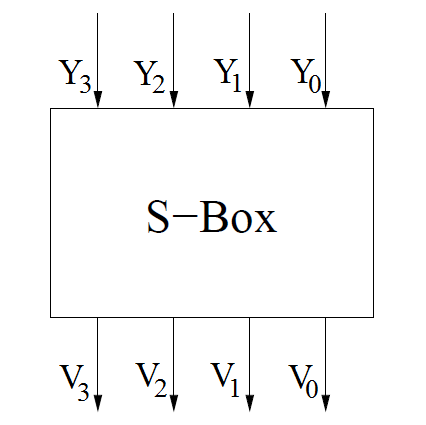
Рисунок 6. Схема S-блока
Для каждого из них выполняются следующие линейные соотношения:
-
S11 :
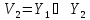 выполняется
с преобладанием
выполняется
с преобладанием
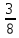
-
S14:
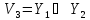 выполняется
с преобладанием
выполняется
с преобладанием
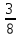
-
S21 :
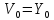 выполняется
с преобладанием
выполняется
с преобладанием
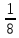
-
S22:
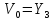 выполняется
с преобладанием
выполняется
с преобладанием
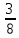
-
S34 :
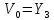 выполняется
с преобладанием
выполняется
с преобладанием
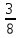
Для каждого из блоков сложения используем следующие соотношения:
-
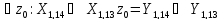 выполняется
с преобладанием больше
выполняется
с преобладанием больше
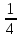
-
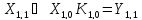 выполняется
с преобладанием
выполняется
с преобладанием
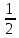
-
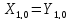 выполняется
с преобладанием
выполняется
с преобладанием
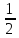
-
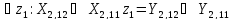 выполняется
с преобладанием больше
выполняется
с преобладанием больше
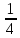
-
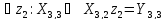 выполняется
с преобладанием больше
выполняется
с преобладанием больше
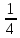
-
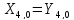 выполняется
с преобладанием
выполняется
с преобладанием
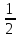
Итоговое соотношение имеет вид:
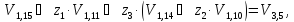 (9)
(9)
где Vij – j-й выход i-го слоя S-блоков.
Согласно
лемме о накапливании, соотношение (9) на
истинном ключе выполняется с преобладанием
больше чем
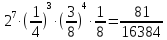 соответственно для проведения
криптоанализа в худшем случаи будет
достаточно иметь порядка 40 тысяч пар
открытый текст – шифртекст. Для проведения
анализа необходимо перебрать 1 бит
первого подключа, и 4 бита пятого, а также
значения
соответственно для проведения
криптоанализа в худшем случаи будет
достаточно иметь порядка 40 тысяч пар
открытый текст – шифртекст. Для проведения
анализа необходимо перебрать 1 бит
первого подключа, и 4 бита пятого, а также
значения
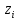 (
(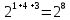 ).
В среднем же 10 тысяч пар открытый текст
- шифртекст более чем достаточно.
).
В среднем же 10 тысяч пар открытый текст
- шифртекст более чем достаточно.
Ход криптоаналиаза:
-
Для восстанавливаемого ключа сгенерировать 10000 случайных пар открытый текст – шифртекст
-
Для сгенерированных пар и всевозможных значений части ключа
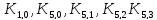 и параметров
и параметров
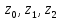 вычислить преобладание, с которым
выполняется соотношение 9
вычислить преобладание, с которым
выполняется соотношение 9 -
Значения части ключа, на котором соотношение 9 выполняется с наибольшим преобладанием, с высокой долей вероятности совпадает с соответствующими битами искомого ключа. Если не удается однозначно выделить искомый подключ, то генерируем еще 10000 случайных пар открытый текст – шифртекст и возвращаемся к шагу 3
-
Оставшиеся биты находим тотальным опробованием
