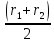Domashnee_zadanie_TD_2

Условия задания. В задании необходимо рассчитать стационарное температурное поле осесимметричной многослойной цилиндрической стенки, во втором слое которого равномерно распределен внутренний источник тепла удельной мощностью (рис. 1), определить потоки при и , а так же построить график изменения температуры по толщине стенки.

Рис. 1

Дано: , , , , , , , , , , .

Решение задачи производим в программе MathCAD.

Вводим начальные условия:

Составляем уравнения температурного поля:

По граничным условиям I-го и III-го рода составляем систему уравнений и решаем ее с помощью блока Given-Find.

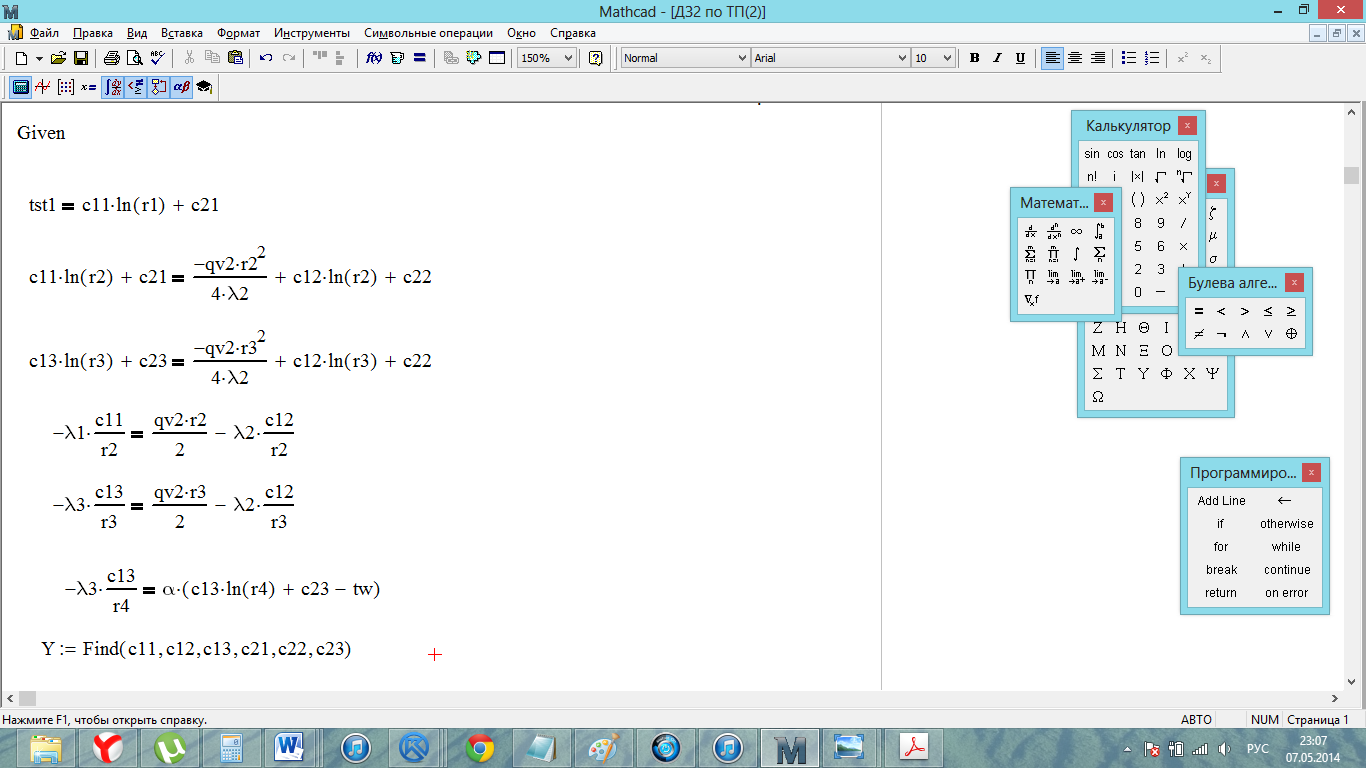
Матрица Y содержит искомые коэффициенты.

По результатам вычислений коэффициенты уравнений равны (размерность [К]):

Тепловые потоки при при и 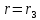равны (размерность ):

График изменения температуры по толщине стенки приведен на рис.2.

Т, К

Рис. 2

r, мм

Результаты вычислений приведены в таблице 1.

Таблица 1

Координата	м
T	K	873	873.21	873.41	872.191	861.226	772.02	694.747

Максимум температурного ([K]) поля находим с помощью функции Minimize.ц