- •Глава 1. Введение ...2
- •Глава 1. Введение
- •1.1. Общая проблема
- •1.2. Структура работы
- •1.3. Цель работы
- •1.4. Состояние вопроса
- •1.5. Задача об изгибе пластинки переменной толщины
- •Глава 2. Вывод основных уравнений изгиба круглых симметрично нагруженных пластин
- •2.1. Принятые допущения
- •2.2. Пластина под действием осесимметричной деформации
- •2.2.1. Определение деформаций и напряжений
- •2.2.2. Определение усилий и моментов
- •2.2.3. Связь деформаций и напряжений с заданными усилиями и моментами
- •2.2.4. Условия равновесия элемента пластинки
- •2.3. Уравнение осесимметричного изгиба пластинки переменной толщины
- •2.3.1. В общем случае
- •2.3.2. При постоянных по толщине параметрах упругости
- •2.4. Вывод формул для ограничений
- •2.5. Граничные условия
- •Глава 3. Алгоритм оптимизации диска методом чувствительности
- •3.1. Вывод вариационного уравнения
- •3.2. Расчет градиентов целевой функции и ограничений
- •3.3. Алгоритм метода проекции градиента
- •3.4. Мкэ применительно к задаче об изгибе круглой пластинки
- •3.5. Мкр применительно к задаче об изгибе круглой пластинки
- •Глава 4. Результаты оптимизации
- •4.1. Описание программы
- •4.2. Примеры расчетов оптимальных дисков
- •Глава 5. Организационно-экономическая часть
- •5.1. Организация и планирование проведения нир2
- •Расчёт трудоёмкости и составление календарного графика
- •5.2. Расчет себестоимости нир4
- •5.3. Итоговые данные
- •Глава 6. Экологическая и промышленная безопасность
- •6.1. Проектирование оптимальных условий труда инженера-программиста
- •6.1.1. Анализ условий труда на рабочем месте
- •6.1.2. Требования к рабочим местам оборудованными пк
- •6.1.3. Требования к пэвм.
- •6.1.4. Требования к помещениям для работы с пэвм
- •6.2. Требования к производственной среде
- •6.2.1. Требования к микроклимату на рабочих местах, оборудованных пэвм
- •6.2.2. Требования к уровням шума и вибрации на рабочих местах, оборудованных пэвм
- •6.2.3. Требования к освещению на рабочих местах, оборудованных пэвм Утомляемость органов зрения зависит от ряда причин:
- •6.2.4. Требования к уровням электромагнитных полей на рабочих местах, оборудованных пэвм
- •6.2.5. Требования к организации режимов труда и отдыха
- •6.2.6. Требования к организации медицинского обслуживания пользователей вдт и пэвм
- •6.3. Определение освещенности
- •6.3.1. Описание помещения, в котором располагается рабочее место
- •Расчет систем искусственного освещения
- •6.4. Ртутьсодержащие отходы потребления и их утилизация
- •6.5. Характеристики ламп
3.4. Мкэ применительно к задаче об изгибе круглой пластинки
Расчет диска ведется методом конечных элементов (МКЭ) [9]. МКЭ позволяет избежать численного интегрирования, тем самым уменьшая погрешность вычислений, что, как следствие, приводит к повышению точности. Так же МКЭ позволяет рассчитывать диск на небольшом количестве узлов, что приводит к относительному уменьшению затрат ресурсов вычислительной машины.
Разобьем
весь диск на конечные элементы. В расчетах
для перехода от функции
 к вектору параметров проектирования
к вектору параметров проектирования использовалась линейная аппроксимация.
Отрезок
использовалась линейная аппроксимация.
Отрезок разбивается на
разбивается на равных интервалов
равных интервалов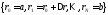 ,
для аппроксимации управляющей функции
использовались линейные функции.
,
для аппроксимации управляющей функции
использовались линейные функции.
Рассмотрим систему (2.24) дифференциальных уравнений первого порядка для диска. Введем обозначения

 (3.23)
(3.23)
И интегрируя по радиусу, получим соотношения МКЭ для уравнения в перемещениях для диска:

Рассмотрим формирования матрицы системы и вектора нагрузок:

 -
матрица формы, где
-
матрица формы, где
 .
.
Суммируя по всем конечным элементам, найдем

Обозначим

тогда можно записать

 -
матрица жесткости для одного элемента.
-
матрица жесткости для одного элемента.
Матрица
и правая часть для всей системы
формулируются из
 и
и как показано на рис. 3.2.
как показано на рис. 3.2.
|
|
|
Рис. 3.2. Формирование общей матрицы системы |
3.5. Мкр применительно к задаче об изгибе круглой пластинки
Замена краевой задачи начальной приводит к существенному упрощению решения. Поэтому другой удобный метод решения краевой задачи (2.24) и сопряженной системы (3.15) - метод начальных параметров, основанный на дополнении поставленных для краевой задачи граничных условий в начале участка интегрирования некоторыми параметрами, называемыми начальными [13]. Эти параметры выбираются так, чтобы полученная при этом совокупность начальных условий полностью определяла решение поставленной задачи.
Основная
трудность численного решения уравнений
(2.24), (3.15) заключается в том, что на
основании граничных условий в начальной
точке ( )
бывают известны только некоторые
начальные значения функций
)
бывают известны только некоторые
начальные значения функций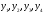 (
( в случае сопряженной системы). Остальные
же должны быть определены по граничным
условиям на наружном крае пластины (
в случае сопряженной системы). Остальные
же должны быть определены по граничным
условиям на наружном крае пластины ( )
[12].
)
[12].
Пусть дана краевая задача (2.24) с граничными условиями (2.31).
Общий интеграл системы (2.24)
 (3.24)
(3.24)
где
 - частное решение матричного уравнения
(2.24), удовлетворяющее нулевым начальным
условиям
- частное решение матричного уравнения
(2.24), удовлетворяющее нулевым начальным
условиям ;
; -
- -е
частное решение соответствующего
уравнению (2.24) однородного уравнения
-е
частное решение соответствующего
уравнению (2.24) однородного уравнения ,
т.е. при нулевом столбце свободных членов
,
т.е. при нулевом столбце свободных членов
 ,где
,где
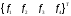 взято из формулы (3.23),
взято из формулы (3.23),
удовлетворяющее начальным условиям:

 -
постоянные интегрирования.
-
постоянные интегрирования.
Подстановкой
полученного по (3.24) решения в условия
(2.31) получают систему
 -х
алгебраических уравнений для определения
-х
алгебраических уравнений для определения .
.
Например, для пластины с шарнирной опорой на внутреннем краю:

коэффициенты равны:



Найденные постоянные подставляют в (3.24), откуда находят решение исходной краевой задачи (2.24), (2.31).
Аналогично
решается сопряженная задача (3.15). В ней
коэффициенты
 для граничных условий вида:
для граничных условий вида:
будут равны:

Глава 4. Результаты оптимизации
4.1. Описание программы
Для реализации поставленной задачи была написана программа с использованием языка программирования СИ.
Данная
программа проводит оптимизацию диска
с помощью МКЭ и МКР. Способ расчета можно
выбрать до начала работы программы. На
вход подаются все данные о материале
диска, такие как модуль упругости
 ,
коэффициент Пуассона
,
коэффициент Пуассона ,
плотность
,
плотность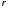 и температурный коэффициент
и температурный коэффициент ;
так же данные о размерах диска – внешний
и внутренний радиусы и толщина; и,
наконец, данные о нагрузке на диск –
приложенная распределенная сила,
температурный градиент и моменты. Так
же в программе можно задать ограничение
на минимальную и максимальную толщину
диска.
;
так же данные о размерах диска – внешний
и внутренний радиусы и толщина; и,
наконец, данные о нагрузке на диск –
приложенная распределенная сила,
температурный градиент и моменты. Так
же в программе можно задать ограничение
на минимальную и максимальную толщину
диска.
Перед началом работы программы нужно задать значения управляющих параметров:
 -
количество узлов (точек, находящихся
на равном расстоянии по всей длине
диска);
-
количество узлов (точек, находящихся
на равном расстоянии по всей длине
диска);
 и
и
 - отвечают за норму изменения толщины
на каждой итерации;
- отвечают за норму изменения толщины
на каждой итерации;
 -
отвечает за сглаживание функции толщины
диска.
-
отвечает за сглаживание функции толщины
диска.
 -
отвечает за норму отклонения получившегося
напряжения в точке от допустимого
напряжения.
-
отвечает за норму отклонения получившегося
напряжения в точке от допустимого
напряжения.
Все эти пять параметров сильно влияют на скорость и характер сходимости алгоритма.
Алгоритм можно запустить с двумя способами останова:
До полной его сходимости с заданной точностью.
В этом случае количество итераций определяется программой автоматически и на выходе получается форма диска, которая в большей или меньшей степени удовлетворяет всем заданным параметрам.
Задать на входе количество итераций.
В этом случае программа проведет нужное количество итераций и на выходе получается форма диска, которая необязательно будет удовлетворять всем ограничениям. При таком запуске удобно смотреть текущее состояние диска и скорость сходимости. Так же, при желании можно посмотреть результаты работы алгоритма после того как оптимальная форма уже найдена (для этого необходимо задать количество итерации больше, чем необходимо для сходимости алгоритма).
После
завершения работы программы можно
посмотреть результаты расчетов всех
требуемых параметров, например и их графики в зависимости от
и их графики в зависимости от .
.
При реализации алгоритма предполагалось, что расчет диска будет вестись только методом конечных элементов, но, после проведения первых расчетов стала ясна непригодность этого подхода. В результатах оптимизации были явно выражены биения почти всех ключевых функций. Вследствие этого пришлось отдать предпочтение менее точному на малом количестве узлов методу конечных разностей. Но увеличение количества узлов в данном случае не привело к значительному увеличению времени расчета программой, так как время одной итерации МКР значительно меньше времени одной итерации МКЭ.