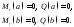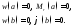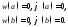- •Глава 1. Введение ...2
- •Глава 1. Введение
- •1.1. Общая проблема
- •1.2. Структура работы
- •1.3. Цель работы
- •1.4. Состояние вопроса
- •1.5. Задача об изгибе пластинки переменной толщины
- •Глава 2. Вывод основных уравнений изгиба круглых симметрично нагруженных пластин
- •2.1. Принятые допущения
- •2.2. Пластина под действием осесимметричной деформации
- •2.2.1. Определение деформаций и напряжений
- •2.2.2. Определение усилий и моментов
- •2.2.3. Связь деформаций и напряжений с заданными усилиями и моментами
- •2.2.4. Условия равновесия элемента пластинки
- •2.3. Уравнение осесимметричного изгиба пластинки переменной толщины
- •2.3.1. В общем случае
- •2.3.2. При постоянных по толщине параметрах упругости
- •2.4. Вывод формул для ограничений
- •2.5. Граничные условия
- •Глава 3. Алгоритм оптимизации диска методом чувствительности
- •3.1. Вывод вариационного уравнения
- •3.2. Расчет градиентов целевой функции и ограничений
- •3.3. Алгоритм метода проекции градиента
- •3.4. Мкэ применительно к задаче об изгибе круглой пластинки
- •3.5. Мкр применительно к задаче об изгибе круглой пластинки
- •Глава 4. Результаты оптимизации
- •4.1. Описание программы
- •4.2. Примеры расчетов оптимальных дисков
- •Глава 5. Организационно-экономическая часть
- •5.1. Организация и планирование проведения нир2
- •Расчёт трудоёмкости и составление календарного графика
- •5.2. Расчет себестоимости нир4
- •5.3. Итоговые данные
- •Глава 6. Экологическая и промышленная безопасность
- •6.1. Проектирование оптимальных условий труда инженера-программиста
- •6.1.1. Анализ условий труда на рабочем месте
- •6.1.2. Требования к рабочим местам оборудованными пк
- •6.1.3. Требования к пэвм.
- •6.1.4. Требования к помещениям для работы с пэвм
- •6.2. Требования к производственной среде
- •6.2.1. Требования к микроклимату на рабочих местах, оборудованных пэвм
- •6.2.2. Требования к уровням шума и вибрации на рабочих местах, оборудованных пэвм
- •6.2.3. Требования к освещению на рабочих местах, оборудованных пэвм Утомляемость органов зрения зависит от ряда причин:
- •6.2.4. Требования к уровням электромагнитных полей на рабочих местах, оборудованных пэвм
- •6.2.5. Требования к организации режимов труда и отдыха
- •6.2.6. Требования к организации медицинского обслуживания пользователей вдт и пэвм
- •6.3. Определение освещенности
- •6.3.1. Описание помещения, в котором располагается рабочее место
- •Расчет систем искусственного освещения
- •6.4. Ртутьсодержащие отходы потребления и их утилизация
- •6.5. Характеристики ламп
2.4. Вывод формул для ограничений
Ограничения на эквивалентные напряжения из формулы (1.1) представим в виде
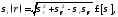 (2.27)
(2.27)
где
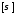 - допускаемое напряжение на радиусе,
- допускаемое напряжение на радиусе,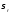 и
и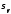 выражаются из уравнений (2.5), (2.17) и
(2.22):
выражаются из уравнений (2.5), (2.17) и
(2.22):
 (2.28)
(2.28)
При постоянных по толщине параметрах упругости и при линейном изменении температуры по толщине диска [2]:
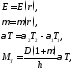 (2.29)
(2.29)
где
 - температурные деформации на поверхности
диска, (2.28) примет вид
- температурные деформации на поверхности
диска, (2.28) примет вид
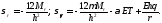 (2.30)
(2.30)
2.5. Граничные условия
Задача (2.24) является краевой и состоит из четырех дифференциальных уравнений первого порядка. Следовательно, должны быть заданы четыре краевых условия: два – на внутреннем радиусе и два – на внешнем [13]:
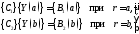 (2.31)
(2.31)
где
 ;
;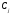 и
и - матрицы столбцы размером
- матрицы столбцы размером :
: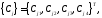
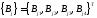 ,
,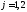 .
.
Например,
в книге [1] предлагается задать два
статических параметра на внутреннем
радиусе
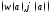 ,
а на внешнем радиусе – два динамических
параметра
,
а на внешнем радиусе – два динамических
параметра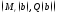 .
.
В
примерах [2] граничными условиями
определяется поперечная сила на обоих
радиусах
 и задаются угол поворота нормали на
внутреннем радиусе и момент на внешнем.
и задаются угол поворота нормали на
внутреннем радиусе и момент на внешнем.
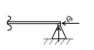
Рассмотрим отдельно разные способы опирания пластины на контуре [12]:
свободный край;
свободно опертый край;
жестко защемленный край.
При
жестком закреплении нет угловых и
линейных перемещений
 .
.
Свободное опирание (подвижная/неподвижная шарнирные опоры) исключает линейное перемещение в вертикальном направлении, но при этом возможен поворот по опертой стороне.
Способы задания граничных условий приведены в табл. 2.1.
|
|
Таблица 2.1 | |||
|
Способы задания граничных условий | ||||
|
на внешнем радиусе
на внутреннем радиусе
|
свободный край |
свободное опирание пластины на контуре1 |
жестко защемленный край | |
|
|
|
| ||
|
свободный край |
|
|
| |
|
| ||||
|
свободное опирание пластины на контуре1 |
|
|
| |
|
| ||||
|
жестко защемленный край |
|
|
| |
|
| ||||
Глава 3. Алгоритм оптимизации диска методом чувствительности
3.1. Вывод вариационного уравнения
После того как получена система уравнений для расчета пластинки можно переходить к алгоритму оптимизации диска. Для удобства заменим ограничение (1.1) интегральным соотношением [6]:
 (3.1)
(3.1)
где
принято обозначение
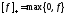 для любой функции
для любой функции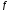 .
.
Метод
оптимизации заключается в оценке
чувствительности функции цели к параметру
управления, которым в нашей задаче
является толщина диска [5]. Для реализации
этого метода следует взять два похожих
диска cтолщинами и
и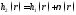 .
Отметим, что переход от вектора состояния
.
Отметим, что переход от вектора состояния к вектору
к вектору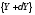 изменит операторное уравнение (2.24)
изменит операторное уравнение (2.24)
 (3.2)
(3.2)
где

 .
.
Тогда
представим матрицу
 :
:
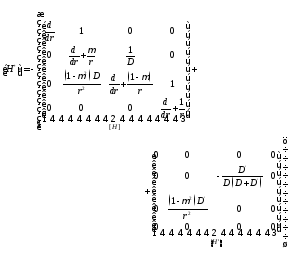 (3.3)
(3.3)
Покажем,
что
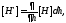 где
где Производная от всех элементов матрицы
Производная от всех элементов матрицы будет равна 0, кроме
будет равна 0, кроме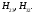 Рассмотрим дифференцирование этих
элементов отдельно:
Рассмотрим дифференцирование этих
элементов отдельно:
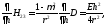 (3.4)
(3.4)
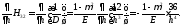 (3.5)
(3.5)
Теперь
распишем значения ненулевых элементов
матрицы
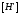 с учетов
с учетов :
:
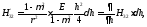 (3.6)
(3.6)
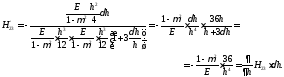 (3.7)
(3.7)
Из
(3.5) и (3.6) следует, что
 Аналогично получим
Аналогично получим
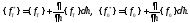
Таким
образом, вариационная постановка задачи
будет иметь следующий вид: (3.8)
(3.8)
Исключая из (3.8) уравнение (2.24), соответствующее начальному состоянию, получим:
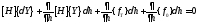
или уравнение в вариациях имеет вид
 (3.9)
(3.9)
где
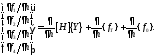 (3.10)
(3.10)
Граничные
условия из (2.31) для
 получим следующие
получим следующие
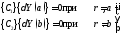 (3.11)
(3.11)