1.5. Задача об изгибе пластинки переменной толщины

Задача оптимизации круглой пластинки заключается в минимизации ее массы при выполнении ограничений на напряженно-деформированное состояние. В простейшем случае геометрия пластинки задается функцией толщины от радиуса которая и является параметром управления.

Функцией качества, подлежащей минимизации, является масса пластинки. Для обеспечения технологичности конструкций, на проект пластинки накладываются геометрические или технологичные ограничения Требование работоспособности конструкции выражается в прочностном ограничении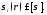Все эти требования к проекту пластинки составляют оптимизационную задачу

(1.1)

здесь плотность материала пластинки;внутренний радиус пластинки;внешний радиус пластинки;конструктивные и технологические ограничения на толщину пластинки;интенсивность напряжений;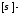допускаемые напряжения.

В данной работе рассматривается круглая изотропная пластинка (далее в качестве примера круглой пластины будем рассматривать диск ГТД, см. рис. 1) симметричная относительно своей срединной поверхности. Толщина предполагается малой по сравнению с наружным радиусом. Силы, действующие на диск, равномерно распределены по поверхности и направлены перпендикулярно радиусу. Температура считается постоянной по толщине.

Напряженное состояние в пластинке считается двумерным и осесимметричным, напряжения равномерно распределены по толщине.

Рис. 1.1. Меридиональное сечение диска, симметричного относительно своей срединной поверхности

Далее будут рассмотрены расчет напряженно-деформированного состояния круглой пластины и вывод формул для алгоритма оптимизации методом проекции градиента.

Глава 2. Вывод основных уравнений изгиба круглых симметрично нагруженных пластин

2.1. Принятые допущения

Теория изгиба пластин и оболочек основана на некоторых упрощающих предположениях [1]:

1. толщина пластинки 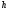достаточно мала по сравнению с другими ее размерами, что значит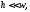где- прогиб пластинки;

2. гипотеза Кирхгофа (о неизменности нормали) гласит, что точки, расположенные на некоторой прямой, нормальной к срединной поверхности до деформации, после деформации снова образуют прямую, нормальную к деформированной поверхности;

3. нормальные напряжения в сечениях параллельных срединной поверхности малы по сравнению с изгибными напряжениями, т.е. отсутствует надавливание между слоями пластины.

2.2. Пластина под действием осесимметричной деформации

2.2.1. Определение деформаций и напряжений

С учетом указанных допущений при осесимметрической деформации (рис. 2.1) точки пластинки получают радиальные смещения [6]

(2.1)

где радиальное смещение,угол поворота нормали в точках основной поверхности.

Рис. 2.1. Прогиб пластины

Радиальная и окружная деформация равны

(2.2)

или

(2.3)

где

- векторы деформации основной поверхности и кривизны.

При упругом деформировании изотропного материала имеем

(2.4)

В последнем равенстве вектор напряжений,вектор дополнительных деформаций,температурная деформация. Матрица упругости материала

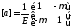
Как и раньше, модуль упругости,коэффициент Пуассона. Из равенств (2.4) и (2.3) вытекает

(2.5)

где

- матрица жесткости материала,

(2.6)

- условные дополнительные (начальные) напряжения. По физическому смыслу напряжения соответствуют (с обратным знаком) дополнительным деформациямпри полном стеснении плоской деформации элемента.