
- •1.27 1. Программы линейной структуры
- •1. Программы линейной структуры
- •Средства разработки программ линейной структуры
- •Целые типы данных
- •Вещественные типы данных
- •Стандартные функции для обработки числовых данных
- •Арифметические выражения
- •Оператор присваивания
- •Ввод данных с клавиатуры
- •Вывод данных в окно программы
- •Приемы, используемые для минимизации вычислений
- •Пример 1.1 выполнения задания
- •Пример 1.2 выполнения задания
- •Задания 1.1 для самостоятельной проработки
- •Задания 1.2 для самостоятельной проработки
Задания 1.1 для самостоятельной проработки
В заданиях 1 – 28:
вычислить, упростив за счет использования скобочных форм и/или дополнительных переменных, значения по заданным формулам,
для контроля правильности результатов выполнить вычисления по формулам без использования скобочных форм и дополнительных переменных,
проверить результаты на комбинациях заданных значений аргументов и при возникновении исключений дополнить программу обработкой этих исключений с выводом типа исключения и предложением закончить выполнение программы нажатием клавиши Enter.
 X=(2;
-2), Y=( 4; -3).
X=(2;
-2), Y=( 4; -3).B=A+2; C=(A+3)/(A+2); D=(A+4)/(A+3); E=(A+5)/(A+4); A=(1; 2; -2; 3; 4).
 ;
X=(0; 1; 2; -2; 4).
;
X=(0; 1; 2; -2; 4).B=sinA; C=lgA; D=eA; E=|A|; S=(A+B)(A+B+C)(A+B+C+D)(A+B+C+D+E); A=(8; -2; 4; -5).
B=A+5; C=A-2; D=B+C; E=A-C;
 A=(-15; -5; 0; 7; 14).
A=(-15; -5; 0; 7; 14).B=A-2; C=A+3; D=B+C; E=A-2; P1=A·B; P2=A·B·C; P3=A·B·C·D; P4=A·B·C·D·E; A=(-4; 0; 4; 7).
 X=(-9;
-4; 0; 3; 9).
X=(-9;
-4; 0; 3; 9). X=(-3; 5), A=(-3;5).
X=(-3; 5), A=(-3;5). X=(-3; 0; 3), A=4.
X=(-3; 0; 3), A=4. X=(-7; -2; 0; 2; 7).
X=(-7; -2; 0; 2; 7). X=(0,5; 1; 2), A=4, B=3.
X=(0,5; 1; 2), A=4, B=3. X=(2,5;
5; 7; 10), A=4, B=3.
X=(2,5;
5; 7; 10), A=4, B=3. X=(1; 2,5; 5; 7; 10).
X=(1; 2,5; 5; 7; 10). X=(-0,5; 5; 10; 25).
X=(-0,5; 5; 10; 25). X=(-15; -5; -2; 2; 5).
X=(-15; -5; -2; 2; 5). X=(-5; -2; 2; 5).
X=(-5; -2; 2; 5). X=(0; 30 o;
45 o;
60 o;
90 o).
X=(0; 30 o;
45 o;
60 o;
90 o).
 X=(0; 1; 2; 3).
X=(0; 1; 2; 3). X=(0,001; 0,1; 0,3; 0,5; 0,9; 1,8).
X=(0,001; 0,1; 0,3; 0,5; 0,9; 1,8). X=(0,001; 0,02; 0,1; 0,9).
X=(0,001; 0,02; 0,1; 0,9). X=(0,001 o;
15 o
; 30 o;
60 o;
135 o).
X=(0,001 o;
15 o
; 30 o;
60 o;
135 o). X=(0,001o;
15 o
; 30 o;
60 o;
270 o).
X=(0,001o;
15 o
; 30 o;
60 o;
270 o). X=(-5; -2; 2; 5).
X=(-5; -2; 2; 5). X=(0,001; 0,1; -1; 1; 4).
X=(0,001; 0,1; -1; 1; 4). X=(0,001; 0,1; -1; ; 1
4), A=3.
X=(0,001; 0,1; -1; ; 1
4), A=3. X=(0,001; 0,1; 1; 4), A=1,5.
X=(0,001; 0,1; 1; 4), A=1,5.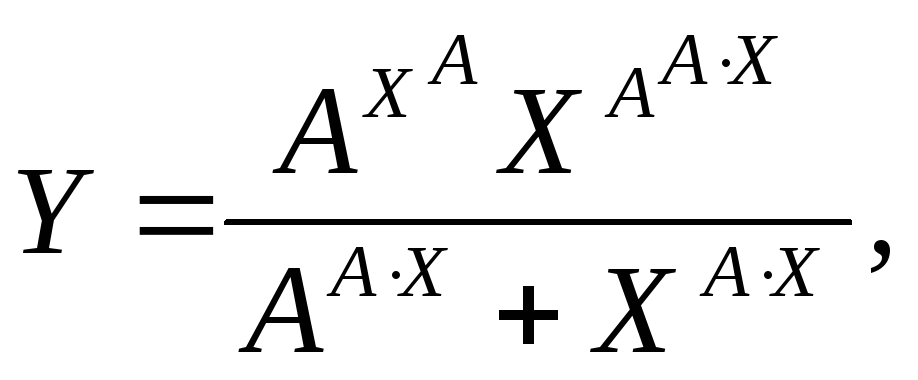 X=(0,001;
0,1; 1; 4) и A=2.
X=(0,001;
0,1; 1; 4) и A=2. X=(-4; 0; 4; 11).
X=(-4; 0; 4; 11).
В заданиях 29 и 30 найти коэффициенты k0, k1, k2, … представления числа Х (0≤X<PN) в позиционной системе счисления с основаниемP, используя операцииmodиdiv. Для контроля результатов выполнить вычисление Х непосредственно по заданной формуле разложенияXпо степенямPдля найденных коэффициентов, а также после преобразования выражения в формуле по схеме Горнера. Вывести все результаты вычислений в наглядной форме с поясняющими текстами. Проверить работу программы при вводимых значениях X из набора М.
P=8, N=4,
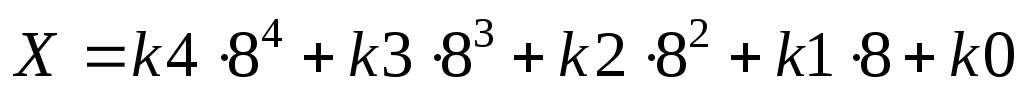 ,
M={0; 1; 2; 4; 7, 8; 65; 1023; 4095}.
,
M={0; 1; 2; 4; 7, 8; 65; 1023; 4095}.P=16, N=3,
 ,
M={0; 1; 15; 64; 127; 255; 2047; 4095}.
,
M={0; 1; 15; 64; 127; 255; 2047; 4095}. Найти среднее геометрическое абсолютных значений частных от целочисленного деления X, X2, X3 на Y и среднее арифметическое остатков от целочисленного деления X, X2, X3 на Y. Для контроля результатов целочисленного деления выводить на экран с поясняющими надписями делимое, делитель, частное, абсолютное значение частного, остаток. Также с поясняющими текстами вывести найденные средние геометрические и средние арифметические. Проверить работу программы при вводе значений X=(-5; 5) и Y=(-3; 3).
Координаты вершин параллелепипеда заданы положительными значениями X1, X2, Y1, Y2, Z1, Z2 (X1<X2, Y1<Y2, Z1<Z2), имеющими ненулевые дробные части. Требуется найти целочисленные координаты I1, I2, J1, J2, K1, K2 вершин такого параллелепипеда, который находится внутри заданного и имеет наибольший объем. Найти также объемы этих параллелепипедов и отношение объемов. Все значения X1, X2, Y1, Y2, Z1, Z2 и I1, I2, J1, J2, K1, K2 вывести на экран с поясняющими надписями, а найденные объемы и их отношения вывести с предшествующими поясняющими текстами. Проверить работу программы на вводимых X1=(2,7; 5,2), X2=2·X1, Y1=X1-1, Y2=2·Y1, Z1=
 ,
Z2=3·Z1.
,
Z2=3·Z1.
