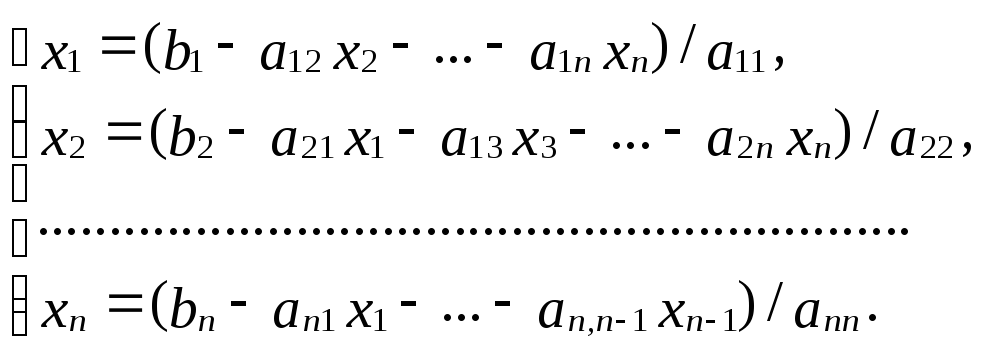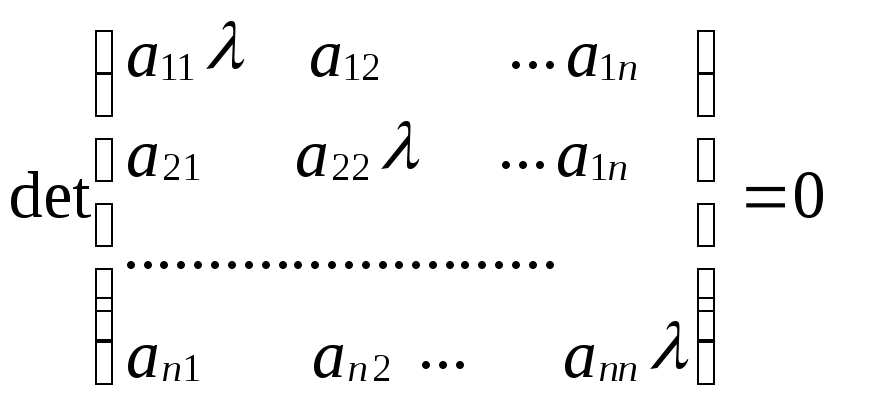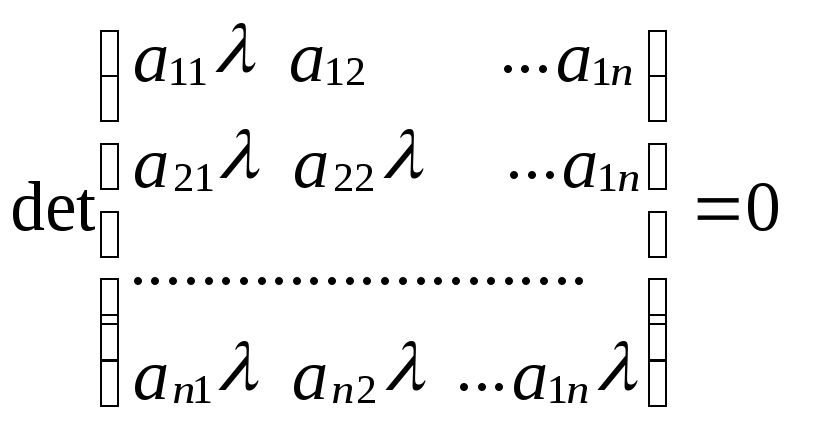2Итерационные методы решения СЛАУ
.doc2. Численные методы решения систем линейных алгебраических уравнений. Итерационные методы
В случае, когда система уравнений имеет большое (103-104) число уравнений, метод Гаусса неэффективен, так как требует большого количества вычислений. Для решения подобных систем предпочтительно применять итерационные методы (методы последовательных приближений).
Для итерационного решения системы
|
|
(31) |
преобразуем ее к виду
|
|
(32) |
Выберем произвольно
начальное приближение
![]() ,
подставим его в правую часть выражения
(32), получим первое приближение
,
подставим его в правую часть выражения
(32), получим первое приближение
|
|
(33) |
Продолжая этот
процесс далее, мы получим последовательность
![]() по формулам
по формулам
|
|
(34) |
|
|
|
В
качестве начального приближения
обычно берут вектор
|
|
При этом возникают следующие вопросы:
Как преобразовать систему (31) к виду (32)?
1. Сходится ли процесс (34) и, если сходится, то к какому вектору?
-
Устойчив ли процесс решения задачи?
-
Когда надо прекращать вычисления?
Возьмем любую невырожденную матрицу D и запишем систему (31) в виде
|
|
(34) |
Очевидно, что все решения системы (31) являются решениями системы (34) и наоборот (системы эквивалентны).
Сравнивая (34) и (32), получим:
![]()
Теорема 1.
(Достаточное условие сходимости). Если
![]() ,
то система уравнений (32) имеет единственное
решение и итерационный процесс (34)
сходится к решению системы (31) со скоростью
геометрической прогрессии.
,
то система уравнений (32) имеет единственное
решение и итерационный процесс (34)
сходится к решению системы (31) со скоростью
геометрической прогрессии.
Рассмотрим различные варианты итерационных процессов.
2.1. Метод простой итерации (Якоби).
Пусть у матрицы
системы (31) все диагональные элементы
не равны 0. Разрешим i
– тое уравнение системы (31) относительно
i
- того переменного, разделив это уравнение
на
![]() .
В результате получим систему
.
В результате получим систему
|
|
(35) |
Запишем систему
(35) в матричном виде. Для этого представим
матрицу A
в следующем виде:
![]() ,
где
,
где
![]() - диагональная матрица.
- диагональная матрица.
Тогда систему (35) можно записать в виде
|
|
(36) |
Определение 11. Метод (36) называется методом простой итерации или методом Якоби.
Условие сходимости
следует из теоремы 1. Все собственные
числа матрицы
![]()
|
|
(37) |
должны быть по модулю меньше 1.
2.2. Метод Зейделя
Для ускорения
процесса простой итерации воспользуемся
методом Зейделя. В процессе вычислений
он использует уже полученные уточненные
значения
![]() .
.
Обозначим через B – нижнюю треугольную матрицу, составленную из элементов матрицы A.
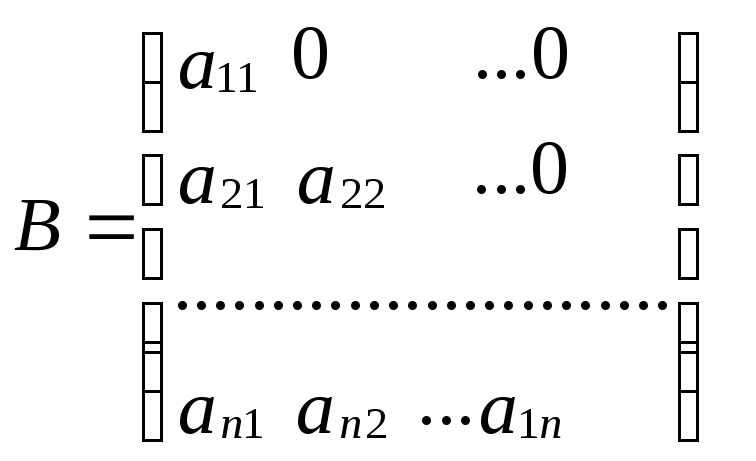 .
.
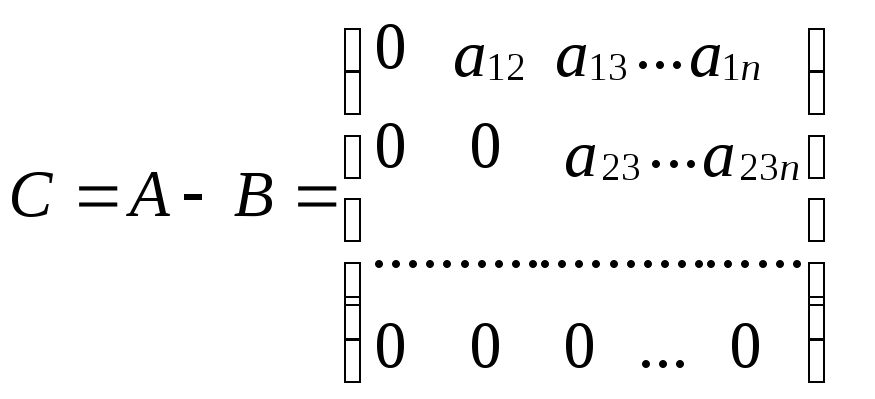 .
.
Представим систему
(31) в виде
![]()
Организуем итерационный процесс по следующей формуле:
![]()
Отсюда получаем
|
|
(38) |
Определение 12. Метод (38) называется методом Зейделя.
Из формулы (28)
видно, что метод Зейделя будет эквивалентен
методу простой итерации с матрицей
![]() ,
поэтому, для его сходимости необходимо
и достаточно, чтобы собственные числа
матрицы
,
поэтому, для его сходимости необходимо
и достаточно, чтобы собственные числа
матрицы
![]() были по модулю меньше 1.
были по модулю меньше 1.
Это условие можно переписать в следующем виде:
Теорема 2. Для сходимости метода Зейделя необходимо и достаточно, чтобы все корни уравнения
|
|
(39) |
были по модулю меньше 1.
Для практического
применения более удобно следующее
условие: существует такое число
![]() ,
что при всех i
выполняется
,
что при всех i
выполняется
![]()
Определение 13. В этом случае говорят, что матрица имеет доминирующую диагональ.
Если система имеет специальный вид, то имеет место еще более удобная теорема.
Теорема 3. Если матрица A симметричная и положительно определенная, то метод Зейделя (38) сходится.
2.3. Метод верхней (нижней) релаксации
Разложим матрицу A на три слагаемых:
D – диагональная матрица,
L – нижняя треугольная матрица,
R – верхняя треугольная.
![]()
Тогда систему (49) можно записать в виде
|
|
(40) |
Умножим (40) на число ω.
![]()
Выразим
![]()
![]()
Перепишем
![]() Тогда
Тогда
![]()
Отсюда получаем итерационный процесс
|
|
(41) |
При ω=1 получаем метод простой итерации.
Определение 13. При ω>1 метод (41) называется методом верхней релаксации. При ω<1 метод (41) называется методом нижней релаксации.
|
|
Можно
показать, что параметр ω
надо выбирать из условия
|
2.4. Общая запись итерационных методов
Итерационные процессы можно описать в общем виде следующей формулой
|
|
(42) |
Здесь
![]() - некоторая матрица, выбираемая для
обеспечения быстрой сходимости метода,
- некоторая матрица, выбираемая для
обеспечения быстрой сходимости метода,
![]() - некоторая система числовых параметров.
- некоторая система числовых параметров.
|
|
Матрицу
|
Определение 14. Запись итерационного метода в виде (42) называется канонической формой записи итерационного метода. [29]
Определение 15.
Процесс
(42) называется
сходящимся,
если
![]() при
при
![]() .
.
Здесь
![]() - точное решение системы (31).
- точное решение системы (31).
Определение 16.
Если
![]() и
и
![]() не зависят от n,
то итерационный процесс называется
стационарным.
В противном случае процесс (42) называется
нестационарным.
не зависят от n,
то итерационный процесс называется
стационарным.
В противном случае процесс (42) называется
нестационарным.
Рассмотрим только этот простой случай.
|
|
(43) |
-
В случае, когда
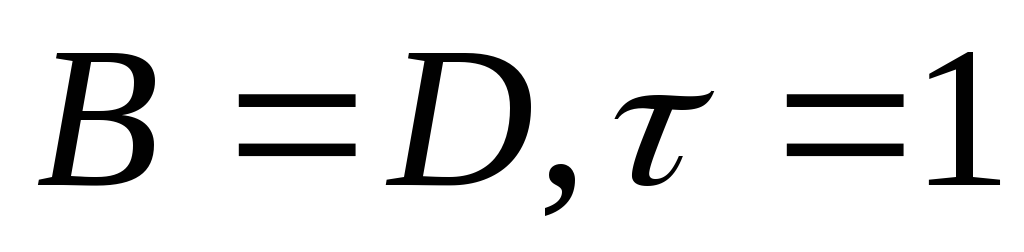 мы получаем метод простой итерации.
мы получаем метод простой итерации. -
В случае, когда
 мы получаем метод Зейделя.
мы получаем метод Зейделя. -
В случае, когда
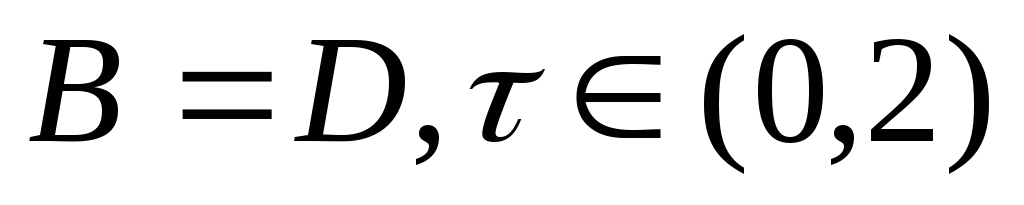 мы получаем метод релаксации.
мы получаем метод релаксации.
Справедлива теорема [29]:
Теорема 4. Пусть A и B – симметричные, положительно определенные матрицы, для которых справедливо неравенство
![]() .
.
|
|
Под
матричным неравенством
|
Тогда при
![]() итерационный метод (43) сходится и для
погрешности справедливы оценки
итерационный метод (43) сходится и для
погрешности справедливы оценки
![]()
где
![]()