Var t : array[1..3] of tPoint; I : byte;
Begin
// Пересчет от реальных декартовых координат на
// пиксельные - экранные. Вот для чего нужна
// наследуемая функция tpix.
for i:=1 to 3 do t[i]:=tpix(apex[i]);
// Установим цвета и рисуем
cnv.Pen.Color:=cl;
cnv.Brush.Color:=cl;
cnv.Polygon(t);
End;
Тестирование классов cDecart и cTri.
Для тестирования создадим обработчик кнопки меню и просто нарисуем прямо на форме треугольник с осями координат.
Листинг 18в. Тестирование классов.
procedure TForm1.N1Click(Sender: TObject);
Var t0 : tPoint; tc : trPoint; tri:cTri;
begin
t0.X:=Form1.ClientWidth div 2;
t0.Y:=Form1.ClientHeight div 2;
tc.x:=0.0;
tc.y:=0.0;
cDecart.Init(t0.x, t0.Y, 100, Form1.Canvas).Draw;
tri:=cTri.Init(t0.x, t0.Y, 100, Form1.Canvas,
0,0, 1,0, 0,1, Tc, clRed);
tri.Draw;
end;
Результат тестирования показан на рис. 18а.
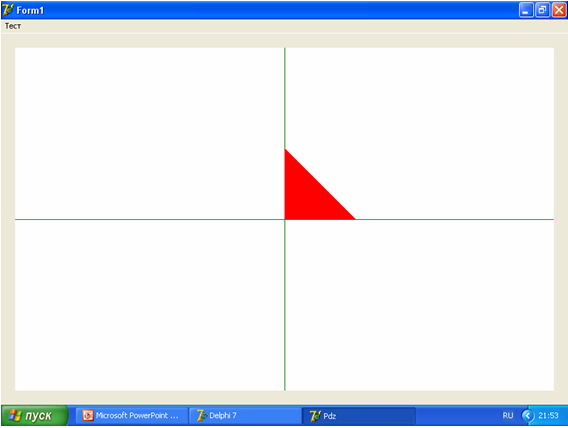
Рис.18а. Примерный вид формы с результатом тестирования.
После тестирования одного треугольника надо выполнить рисование всей фигуры из 4 треугольников, для чего объявить массив треугольников, проинициализировать все его элементы (4), нарисовать их в цикле.
Этап 3. Плоское движение раскладывается на вращательное вокруг центра вращения и поступательное. Метод вращения не рисует повернутый треугольник, он лишь пересчитывает декартовы координаты его вершин. В списке параметров метода передается угол da, на который должен быть повернут треугольник. Объявление в классе (интерфейс метода)
Procedure Rotation(da : real);
Вращение плоской фигуры удобнее всего описывать в полярной системе координат. Более того, иногда в данных класса бывает целесообразно хранить координаты точек в обеих системах, но мы этого делать не будем (оставим для зачета).
Листинг 18г. Реализация метода Rotation.
Procedure cTri.Rotation(da : real);
Var I : byte; r, a : real;
Begin
for i:=1 to 3 do
begin
r:=sqrt(sqr(apex[i].x) + sqr(apex[i].y));
// Надо отдельно рассмотреть случаи 1) нормальный
if apex[i].x > 0 then
a:=arctan(apex[i].y/apex[i].x);
// 2)
if apex[i].x < 0 then a:= ???
// 3а) и 3б)
if apex[i].x = 0 then
if apex[i].y >= 0 then a:=???
else a:=???;
// Наращивание полярного угла
a:=a+da;
// Обратный пересчет на новые декартовы координаты
apex[i].x:=r*cos(a);
apex[i].y:=r*sin(a);
end;
End;
Для случаев, помеченных знаками вопроса, придется вспомнить школьную программу по тригонометрии. На всякий случай вот подсказка: функция arctan() «правильно» работает только в первой и четвертой четверти. На рис.18б представлен результат двух вызовов метода рисования треугольников, между которыми находится вызов метода пересчета.
Рис.18б. Последовательное рисование исходного и повернутого треугольников (см. листинг 18д).
Листинг 18д. Реализация обработчика кнопки.
procedure TForm1.N1Click(Sender: TObject);
Var t0 : tPoint; tc : trPoint;
Begin
// Центр экрана и центр вращения (пока в центре
// экрана)
t0.X:=Form1.ClientWidth div 2;
t0.Y:=Form1.ClientHeight div 2;
tc.x:=0.0; tc.y:=0.0;
// Инициализация объектов
dec:=cDecart.Init(t0.x, t0.Y, 100, Form1.Canvas);
tr[1]:=cTri.Init(t0.x, t0.Y, 100, Form1.Canvas,