
3666
.pdfКвантованное значение Q приближённо представляет истинное значение действительного числа V в виде суммы произведений весовых коэффициентов bi на веса 2i соответствующих двоичных разрядов машинного слова; для беззнаковых чисел с фиксированной точкой определяется формулой
n 1
Q bi 2i .
i 0
Квантованное значение знаковых чисел определяется по формуле
n 2
Q bn 1 2n 1 bi 2i .
i 0
Так как целые числа не имеют дробной части (m = 0), то выражение для V имеет вид
V n 1 bi 2i i 0
и для знакового целого числа:
n 2
V bn 1 2n 1 bi 2i .
i 0
В формате с фиксированной запятой без знака вещественное число V можно считать обозначением полинома
n 1 |
|
|
V S * bi |
2i |
. |
i 0 |
|
|
Например, двоичное число в дополнительном коде 0011.0101 при длине машинного слова n 8 и m = 4 представляет беззнаковое (MSB = 0) вещественное число 3.3125:
11

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 0 * 2 |
7 |
0 * 2 |
6 |
1* 2 |
5 |
1* 2 |
4 |
0 * 2 |
3 |
. |
|||
3.3125 2 |
|
|
|
|
|
|||||||||
|
|
1* 2 |
2 |
0 * 2 |
1 |
1* 2 |
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
При MSB=1 будем иметь уже другое число -4.6875:
4.6875 2 4 1* 27 0 * 26 1* 25 1* 24 0 * 23 1* 22 0 * 21 1* 20 .
1.3. Сумматоры/вычитатели
Рассмотрим схему сумматора, основанного на поразрядном процессе. Обозначим два складываемых числа через A a n-1a n 2 a1a0 и B bn-1bn 2 b1b0 . При сложении двоичных чисел значения цифр в каждом двоичном разряде должны быть сложены между собой с переносом из предыдущего разряда. Если результат при этом превышает 1, то возникает перенос в следующий разряд.
В логической схеме информацию о переносе в разряд i можно представить в виде бита переноса ci , равного 1, если
перенос из предыдущего разряда есть, и 0 – в противном случае. Операция, которую нужно выполнить для каждого
разряда i , будет заключаться в сложении трех битов ai , bi |
и |
|
ci , получении значения бита суммы si |
и переноса |
в |
следующий разряд ci 1 . Фактически ci 1 и si |
представляют |
|
старший и младший разряды в двухразрядной сумме битов ai , bi и ci .
По функциям, заданным в табл. 1.2. Можно построить логические выражения канонические суммы минтермов для суммы si и переноса ci 1 :
si ai bi ci ai bi ci ai bi ci ai bi ci ai bi ci .
ci 1 ai bi ci ai bi ci ai bi ci ai bi ci ai bi ai ci bi ci
12
|
|
|
|
|
|
|
|
|
|
Таблица 1.2 |
|
Определение битов суммы si |
и переноса ci 1 |
по значениям |
|||||||||
|
|
|
|
|
|
ai , bi и ci при сложении |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
a i |
|
bi |
|
ci |
Сумма ai , bi |
и ci |
ci 1 |
|
si |
|
|
0 |
|
0 |
|
0 |
00 |
|
0 |
|
0 |
|
|
0 |
|
0 |
|
1 |
01 |
|
0 |
|
1 |
|
|
0 |
|
1 |
|
0 |
01 |
|
0 |
|
1 |
|
|
0 |
|
1 |
|
1 |
10 |
|
1 |
|
0 |
|
|
1 |
|
0 |
|
0 |
01 |
|
0 |
|
1 |
|
|
1 |
|
0 |
|
1 |
10 |
|
1 |
|
0 |
|
|
1 |
|
1 |
|
0 |
10 |
|
1 |
|
0 |
|
|
1 |
|
1 |
|
1 |
11 |
|
1 |
|
1 |
|
|
|
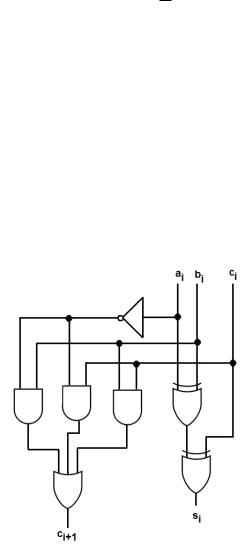
На рис. 1.2 показана схема, реализующая выражения |
|||||||||
для суммы si |
и переноса ci 1 . |
Эта схема называется полным |
|||||||||
сумматором, т.к. она суммирует три бита в разряде, включая перенос. Покаскадно соединив n полных сумматоров можно построить схему для сложения n-разрядных чисел. Разряды двух складываемых чисел подаются на входы a i
результат появляется на выходах si . Последний перенос cn
является старшим разрядом (n+1) – разрядной суммы. Входная линия переноса в младший разряд c0 является еще одним
входом всей схемы. Он позволяет задать начальное значение переноса, что удобно для сложения с многократной точностью.
Сумматоры на схеме рис. 1.3 называют сумматорами с последовательным переносом из-за наличия в них последовательной зависимости от переносов. Каждый полный сумматор в цепочке распространения переносов вносит задержку в двух логических уровнях. Поэтому конечный перенос cn , зависящий от самых правых разрядов a0 , b0 и c0 ,
проходит через 2n логических уровней. Таким образом,
сумматор |
с |
последовательным |
переносом |
работает |
|
|
13 |
|
|

существенно медленнее параллельного сумматора, в котором всего 2 логических уровня.
Рис. 1.2.
Полный
одноразрядный
сумматор
Рис. 1.3. Многоразрядный двоичный сумматор с последовательным переносом
Вычитатель с последовательным переносом можно построить по тому же принципу, что и сумматор. Обозначим
через |
A a n-1a n 2 a1a0 |
уменьшаемое, |
а |
через |
B bn-1bn 2 b1b0 вычитаемое; |
т.е. вычитатель |
должен |
||
выполнять функцию A-B. Заем в соседнем разряде можно считать отрицательным переносом. Таким образом, разряд переноса ci при вычитании может обозначать наличие заема
14
из предыдущего разряда. Операции, которые нужно выполнять в каждом разряде при вычитании, приведены в табл. 1.3. Бит разности обозначен через si .
Сравнивая табл. 1.3 для вычитания и табл. 1.2 для сложения, видим, что колонки для si идентичны. Следовательно, выражения для si в вычитателе и сумматоре
совпадают. Каноническая сумма минтермов для вычитателя имеет вид:
ci 1 ai bi ai ci bi ci .
Полученное выражение совпадает с выражением для сумматора, если a i заменить на a i . На рис. 1.4 показана схема
полного вычитателя, построенного на основе выражений для разности si и переноса ci 1 .
|
|
|
|
|
|
|
|
|
Таблица 1.3 |
Определение |
битов |
разности |
si и переноса ci 1 по |
||||||
значениям ai , bi |
и ci при вычитании |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
a i |
|
|
bi |
|
ci |
ci 1 |
si |
|
|
0 |
|
|
0 |
|
0 |
0 |
0 |
|
|
0 |
|
|
0 |
|
1 |
1 |
1 |
|
|
0 |
|
|
1 |
|
0 |
1 |
1 |
|
|
0 |
|
|
1 |
|
1 |
1 |
0 |
|
|
1 |
|
|
0 |
|
0 |
0 |
1 |
|
|
1 |
|
|
0 |
|
1 |
0 |
0 |
|
|
1 |
|
|
1 |
|
0 |
0 |
0 |
|
|
1 |
|
|
1 |
|
1 |
1 |
1 |
|
Пользуясь сходством булевых выражений для |
|||||||||
сумматоров |
и |
|
вычитателей, |
можно |
построить |
||||
комбинированную схему, которая сможет вычитать и
складывать. |
Для |
этого |
необходимо |
предусмотреть |
управляющий |
вход, |
с помощью которого |
избирательно |
|
|
|
|
15 |
|
инвертировать биты a i в зависимости от требуемой операции. Для избирательной инверсии a i можно применить вентиль Исключающее ИЛИ:
K ai Kai Kai ,
где K - управляющая линия. Если K 0 , то первый член в правой части равен нулю, а второй a i . Если же K 1, то
второй член равен 0, а первый a i . Поэтому выражение K ai соответствует требуемой избирательной инверсии a i . Схема
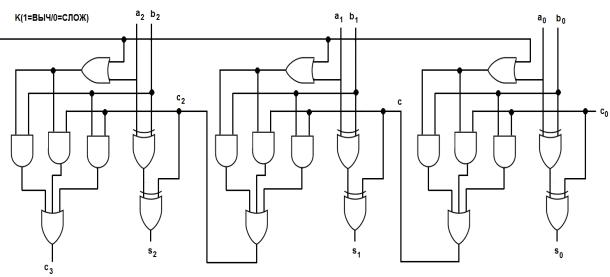
на рис. 1.5 является n-разрядным сумматором/вычитателем с избирательной инверсией a i в схеме вычисления переноса
ci 1 .
Рассмотрим схему сумматора/вычитателя с использованием дополнительного кода. Дополнение можно получить, если прибавить 1 к результату обращения.
Рис. 1.4. Полный одноразрядный вычитатель
16
17
Рис. 1.5. Трехразрядный сумматор/вычитатель, составленный из полных сумматоров/вычитателей
17
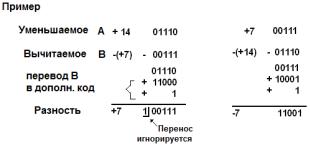
Обращение логически эквивалентно инверсии каждого бита в числе (рис. 1.6). Вентили Исключающее ИЛИ можно применить для избирательной инверсии в зависимости от значения управляющего сигнала. Прибавление 1 к результату обращения можно реализовать, задавая 1 на входе переноса c0 .
Рис. 1.6. Пример вычитания с использованием дополнительного кода (дополнение до двух). Осуществляется инвертирование вычитаемого и суммирование, и переноса 1 в младший значаший разряд с последующим сложением
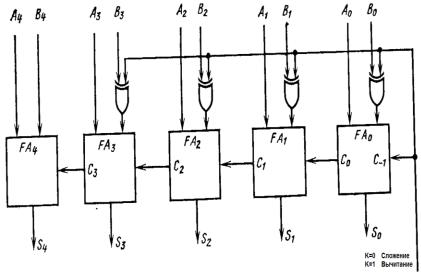
Схема сумматора/вычитателя показана на рис. 1.7. Управляющий сигнал K подается на вентили Исключающее ИЛИ для всех разрядов bi , а также на вход переноса c0 . При
K 1 формируется дополнение B.
Универсальная ИС полного сумматора 9304 представляет собой два полностью независимых полных одноразрядных сумматоров (рис. 1.8). Один из этих сумматоров имеет дополнительный набор входов противоположной полярности. ИС типа 9304 может использоваться для последовательного сложения и для сложения более чем двух переменных. На рис. 1.9 показаны таблицы истинности первого и второго сумматора с условными обозначениями для активно низких и высоких операндов.
18
19
Рис. 1.7. Сумматор/вычитатель, в котором при вычитании второй операнд представляется в дополнительном коде
19
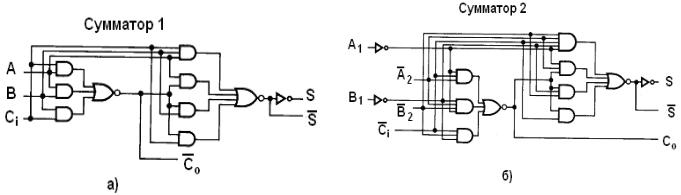
20
Рис. 1.8. Первая (а) и вторая (б) половина сумматора ИС типа 9304
20
