14.3. Несобственные кратные интегралы.

14.3.1. Несобственные интегралы по неограниченной области.Логика определения сходимости несобственного двойного, тройного, - кратного интеграла по неограниченной области такая же, как и для несобственного определённого интеграла: мы ограничиваем область, вычисляем интеграл по этой ограниченной области, и, затем, расширяя область интегрирования до исходной, смотрим, существует или нет конечный предел значения интеграла. Рассмотрим это более подробно для случая двойного интеграла.

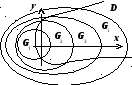
Пусть в неограниченной области D определена функция . Построим бесконечную последовательность ограниченных областей , удовлетворяющую следующим условиям:

1.,

16. 2. ,

17. 3. для любой точки существует такой номер 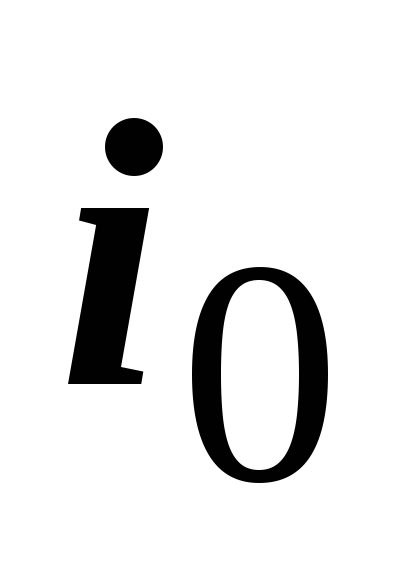, что при .

Пусть теперь . Любая такая область ограничена. Рассмотрим последовательность значений интегралов . Если для любой последовательности существует конечный , то несобственный интеграл называется сходящимся, а значение предела - значением этого интеграла; если хотя бы для одной последовательности не существует или бесконечен, несобственный интеграл называется расходящимся.

Можно показать, что если подынтегральная функция сохраняет знак на области D, то для сходимости достаточно существования конечного для какой-либо одной последовательности . Очевидно, что для таких функций справедливы признаки сравнения. Другое важное свойство, которое мы вводили для сходимости несобственных определенных интегралов, свойство абсолютной сходимости, для кратных интегралов теряет смысл: оказывается, что если сходится , то обязательно сходится и

Рассмотрим два примера.

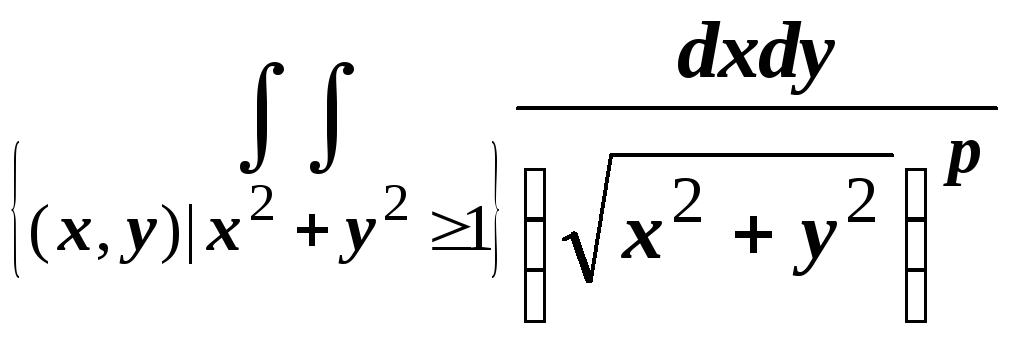1. . Здесь область D - внешность круга радиуса 1. Выберем последовательность (кольца, ограниченные окружностями радиуса 1 и ), тогда , и ( ) . Это выражение имеет конечный предел при , если . Случай исследуется отдельно и приводит к расходимости. Таким образом, исследуемый интеграл сходится при .

Упражнение. Самостоятельно доказать, что сходится при .

2. Цель этого примера - найти значение интеграла, который играет важную роль в теории вероятностей, при решении уравнений в частных производных и в большом числе других приложений - интеграла Пуассона .

Рассмотрим двойной интеграл по всей плоскости . В качестве областей выберем круги радиуса : , и в этом случае . .

С другой стороны, если расписать двойной интеграл 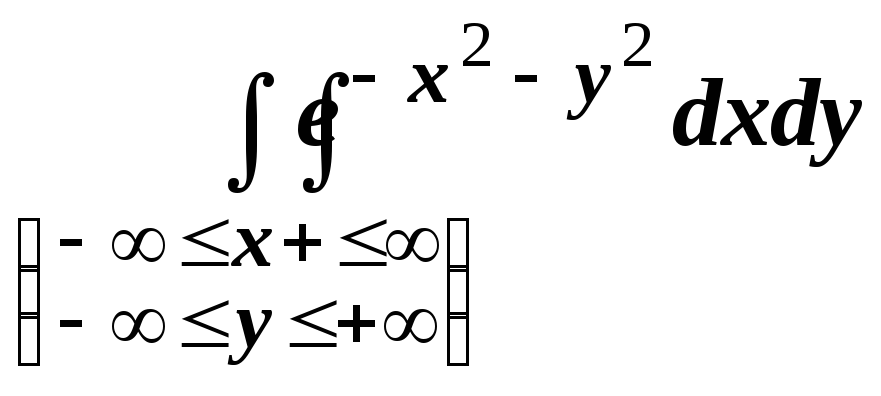в виде повторного, получим , и так как , то .

14.3.2. Несобственные интегралы от неограниченной функции.Структура множества точек, в окрестностях которых функция двух, трех и большего числа переменных может оказаться неограниченной, может быть достаточно сложной. Так, функция трёх переменных может быть неограниченной в окрестности одной точки , прямой , плоскости ; естественно, возможны более сложные случаи. Мы рассмотрим самый простой случай, когда функция неограничена в окрестности единственной точки.

Пусть функция двух переменных определена и непрерывна в ограниченной замкнутой области всюду, за исключением точки . Возьмём бесконечную последовательность ограниченных областей , удовлетворяющую следующим условиям:

1.,

16. 2. ,

Пусть теперь . В каждой такой области функция непрерывна. Рассмотрим последовательность значений интегралов . Если для любой последовательности существует конечный , то несобственный интеграл называется сходящимся, а значение предела - значением этого интеграла; если хотя бы для одной последовательности не существует или бесконечен, несобственный интеграл называется расходящимся.

И в этом случае можно показать, что:

1. если подынтегральная функция сохраняет знак на области D, то для сходимости достаточно существования конечного для какой-либо одной последовательности .

2. Для таких функций справедливы признаки сравнения.

3. Если сходится , то обязательно сходится и

Пример. . Здесь область D - внутренность круга радиуса 1. Выберем последовательность (круги радиуса ), тогда - кольцо , и ( ) . Это выражение имеет конечный предел при , если . Случай исследуется отдельно и приводит к расходимости. Таким образом, исследуемый интеграл сходится при .

Упражнение. Самостоятельно доказать, что сходится при .