
- •16. Кратные, криволинейные, поверхностные интегралы.
- •16.1. Двойной интеграл.
- •16.1.3. Свойства двойного интеграла.
- •16.1.5. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •16.1.6. Задачи на двойной интеграл.
- •16.1.7. Приложения двойного интеграла.
- •16.2. Тройной интеграл.
- •16.2.2.3. Интеграл от единичной функции по области V равен объёму этой области: .
- •16.2.5. Замена переменных в тройном интеграле.
- •14.3. Несобственные кратные интегралы.
- •16.3. Криволинейные интегралы.
- •16.3.2. Криволинейный интеграл первого рода (по длине дуги).
- •16.3.2.4. Механические приложения криволинейного интеграла 1-го рода.
- •16.3.3. Криволинейный интеграл второго рода (по координатам).
- •16.3.3.4. Формула Грина.
- •16.3.3.6. Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути.
- •16.4. Поверхностные интегралы.
- •16.4.3. Поверхностный интеграл первого рода (по площади поверхности).
- •16.4.3.3. Вычисление поверхностного интеграла первого рода.
- •6.4.3.4. Механические и физические приложения поверхностного интеграла 1-го рода.
- •16.4. Поверхностные интегралы.
- •16.4.4. Поверхностный интеграл второго рода (по координатам).
- •17. Теория поля.
- •17.1. Скалярное поле.
- •17.1.2. Частные случаи скалярных полей.
- •17.2. Векторное поле.
- •17.2.2. Дифференциальные характеристики векторного поля.
- •17.2.2.1. Дивергенция векторного поля.
- •17.2.3. Частные случаи векторных полей.
- •17.3.Поток векторного поля через поверхность.
17.3.Поток векторного поля через поверхность.
В разделе 16.4.
Поверхностные интегралы мы
рассмотрели задачу о вычислении
количества жидкости, протекающей через
определённую сторону двусторонней
поверхности ![]() за единицу времени, и получили, что это
количество выражается поверхностным
интегралом
за единицу времени, и получили, что это
количество выражается поверхностным
интегралом ![]() .
Имеется целый ряд физических процессов,
которые описываются аналогичными
поверхностными интегралами, например,
магнитная индукция.
.
Имеется целый ряд физических процессов,
которые описываются аналогичными
поверхностными интегралами, например,
магнитная индукция.
Среди других достоинств математики её мощь заключается, в частности, в способности исследовать процессы в самых разных областях естествознания, абстрагируясь от их физической сущности; приведённые выше примеры показывают естественность введения понятия потока векторного поля через поверхность.
17.3.1.
Определение.
Пусть ![]() - двусторонняя гладкая поверхность,
расположенная в области V,
в которой задано поле
- двусторонняя гладкая поверхность,
расположенная в области V,
в которой задано поле
![]() (M).
Фиксируем выбором нормали
(M).
Фиксируем выбором нормали ![]() одну из двух сторон поверхности
одну из двух сторон поверхности ![]() .
Потоком
векторного поля
.
Потоком
векторного поля
![]() (M)
через поверхность
(M)
через поверхность
![]() называется поверхностный интеграл
первого рода по
называется поверхностный интеграл
первого рода по ![]() от скалярного произведения
от скалярного произведения
![]() (M)
на единичный вектор нормали
(M)
на единичный вектор нормали ![]() к выбранной стороне поверхности: П
к выбранной стороне поверхности: П![]() .
.
Существуют
различные формы записи этого интеграла.
Так как ![]() ,
поток может обозначаться П
,
поток может обозначаться П![]() .
Иногда произведение
.
Иногда произведение ![]() обозначают
обозначают ![]() и называют этот вектор вектором
элементарной площадки, тогда П
и называют этот вектор вектором
элементарной площадки, тогда П![]() .
Если связать
.
Если связать ![]() с проекциями
с проекциями ![]() на координатные плоскости:
на координатные плоскости:
![]()
и использовать
координатную запись поля
![]() ,
то скалярное произведение в координатной
форме даст П
,
то скалярное произведение в координатной
форме даст П![]() ,
т.е. поток может быть выражен и через
поверхностный интеграл второго рода.
Напомню, что в таком интеграле необходимо
выбирать знак каждого слагаемого в
зависимости от знака соответствующей
координаты нормали.
,
т.е. поток может быть выражен и через
поверхностный интеграл второго рода.
Напомню, что в таком интеграле необходимо
выбирать знак каждого слагаемого в
зависимости от знака соответствующей
координаты нормали.
17.3.2. Свойства потока векторного поля. Согласно определению, поток - поверхностный интеграл, поэтому он имеет все свойства поверхностного интеграла. Понятно, что некоторые из этих свойств теряют смысл (интеграл от единичной функции, например), поэтому перечислим основные свойства потока.
Линейность.
 ;
;
2. Аддитивность.
![]() .
Здесь
.
Здесь ![]() и
и ![]() - кусочно-гладкие поверхности, которые
могут пересекаться только по границам;
нормали на этих поверхностях должны
быть согласованы так, чтобы определять
одну сторону всей составной поверхности
- кусочно-гладкие поверхности, которые
могут пересекаться только по границам;
нормали на этих поверхностях должны
быть согласованы так, чтобы определять
одну сторону всей составной поверхности
![]() .
.
3. Поток меняет
знак при изменении стороны поверхности
(так как в каждой точке ![]() вектор
вектор ![]() меняется на -
меняется на -![]() ).
).
17.3.3. Вычисление
потока векторного поля. В
соответствии с определением П![]()
![]() ,
,
поток может
вычисляться и с помощью поверхностного
интеграла первого рода, и с помощью
поверхностного интеграла второго рода.
В примере 2 раздела 16.4.4.3.
Вычисление поверхностного интеграла
второго рода
было приведено вычисление потока поля
![]() через часть плоскости
через часть плоскости ![]() ,
ограниченную координатными плоскостями,
в том и другом представлении. Рассмотрим
более сложный пример.
,
ограниченную координатными плоскостями,
в том и другом представлении. Рассмотрим
более сложный пример.
 Пример.
Найти поток векторного поля
Пример.
Найти поток векторного поля ![]() через полную внешнюю поверхность тела,
ограниченного поверхностями
через полную внешнюю поверхность тела,
ограниченного поверхностями ![]() .
.
Решение.
Поверхность состоит из двух частей: ![]() - часть поверхности параболоида
- часть поверхности параболоида ![]() накрытая шапочкой
накрытая шапочкой ![]() - частью нижней полусферы
- частью нижней полусферы ![]() ;
уровень пересечения этих поверхностей
по оси Oz
определяется уравнением
;
уровень пересечения этих поверхностей
по оси Oz
определяется уравнением
![]() ,
откуда
,
откуда ![]() ;
проекция линии пересечения на плоскость
Oxy
- окружность радиуса
;
проекция линии пересечения на плоскость
Oxy
- окружность радиуса ![]() .
Выпишем нормали:
.
Выпишем нормали: ![]() ;
выбираем знак "+", так как на
;
выбираем знак "+", так как на ![]() нормаль образует тупой угол с осью Oz,
и коэффициент при
нормаль образует тупой угол с осью Oz,
и коэффициент при ![]() должен быть отрицателен (мы находимся
в полупространстве
должен быть отрицателен (мы находимся
в полупространстве ![]() ).
С учётом того, что на
).
С учётом того, что на ![]()
![]() ,
,
![]() ,
,
![]() .
Уравнение
.
Уравнение ![]() в виде поверхности уровня:
в виде поверхности уровня: ![]() ,
,
![]() ,
знак "+", так как угол между
,
знак "+", так как угол между ![]() и осью Oz
острый,
и осью Oz
острый, ![]() .
.
1. Вычисление с
помощью поверхностного интеграла
первого рода: П=П1+П2,
П1![]() ,
П2
,
П2![]() ,
обе поверхности однозначно проектируются
на плоскость Oxy
в круг радиуса
,
обе поверхности однозначно проектируются
на плоскость Oxy
в круг радиуса ![]() ,
поэтому П1
,
поэтому П1
![]()
![]() .
.
П2![]()
![]() .
.
П=П1+П2![]() .
.
2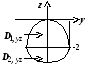 .
Посмотрим, к каким вычислениям приводит
применение поверхностного интеграла
второго рода.
.
Посмотрим, к каким вычислениям приводит
применение поверхностного интеграла
второго рода.![]() .
Для вычисления
.
Для вычисления ![]() придется разбить полную поверхность
придется разбить полную поверхность ![]() на части
на части ![]() ,
находящуюся в полупространстве
,
находящуюся в полупространстве ![]() ,
где
,
где ![]() ,
и
,
и ![]() ,
находящуюся в полупространстве
,
находящуюся в полупространстве ![]() ,
где
,
где ![]() ;
;
![]() (с учётом того, что подынтегральная
функция меняет знак при переходе от
(с учётом того, что подынтегральная
функция меняет знак при переходе от ![]() к
к ![]() )
)
![]()

![]()
![]()
![]() .
.
Интеграл ![]() равен нулю, так как подынтегральная
функция чётна по у,
а интегралы по частям поверхности,
находящихся в полупространствах
равен нулю, так как подынтегральная
функция чётна по у,
а интегралы по частям поверхности,
находящихся в полупространствах ![]() ,
где
,
где ![]() ,
и
,
и ![]() ,
где
,
где ![]() ,
берутся с разными знаками.
,
берутся с разными знаками.
Интеграл ![]() (в соответствии со знаками
(в соответствии со знаками ![]() на
на ![]() и
и ![]() )
)

![]() .
Поток
.
Поток ![]() .
.
Ответы, как и должно быть, совпали, однако вычисления с помощью криволинейного интеграла первого рода оказались существенно более простыми.
17.3.4. Теорема
Остроградского. Пусть
![]() - кусочно-гладкая замкнутая поверхность,
ограничивающая область V,
- кусочно-гладкая замкнутая поверхность,
ограничивающая область V,
![]() - гладкое векторное поле. Тогда поток
поля
- гладкое векторное поле. Тогда поток
поля ![]() через внешнюю сторону
через внешнюю сторону ![]() равен тройному интегралу от дивергенции
поля
равен тройному интегралу от дивергенции
поля ![]() по V:
по V:
![]() .
.
Приведённую выше
формулу обычно называют формулой
Остроградского в векторной форме. Если
записать её в виде
![]() или
или
 ,
то получим формулу Остроградского в
координатной форме. Естественно, для
потока в левой части формулы могут
применяться и другие обозначения.
,
то получим формулу Остроградского в
координатной форме. Естественно, для
потока в левой части формулы могут
применяться и другие обозначения.
 Доказательство.
Достаточно
доказать формулу в случае, когда тело
V
- простое, т.е. проекция V
на любую координатную плоскость -
простая область D,
и любая прямая, перпендикулярная этой
плоскости и проходящая через внутреннюю
точку V,
пересекает границу V
в двух точках. Если V
не является простой областью, мы разобьём
её на простые части; тогда сумма тройных
интегралов по этим частям, в силу
аддитивности, даст интеграл по всей
области V
; а при вычислении поверхностных
интегралов интегралы по введённым
внутренним перегородкам будут браться
дважды с противоположными направлениями
нормали и взаимно уничтожатся. Кроме
того, достаточно доказать формулу
Остроградского для каждого из слагаемых:
Доказательство.
Достаточно
доказать формулу в случае, когда тело
V
- простое, т.е. проекция V
на любую координатную плоскость -
простая область D,
и любая прямая, перпендикулярная этой
плоскости и проходящая через внутреннюю
точку V,
пересекает границу V
в двух точках. Если V
не является простой областью, мы разобьём
её на простые части; тогда сумма тройных
интегралов по этим частям, в силу
аддитивности, даст интеграл по всей
области V
; а при вычислении поверхностных
интегралов интегралы по введённым
внутренним перегородкам будут браться
дважды с противоположными направлениями
нормали и взаимно уничтожатся. Кроме
того, достаточно доказать формулу
Остроградского для каждого из слагаемых:
![]() ,
,
![]() ,
,
 ,
тогда сумма этих формул даст общую
формулу. Докажем, например, что
,
тогда сумма этих формул даст общую
формулу. Докажем, например, что
 .
Простую область V,
как мы знаем, можно описать следующим
образом:
.
Простую область V,
как мы знаем, можно описать следующим
образом: ![]() .
Вычисляем
.
Вычисляем
![]() :
:


![]()
![]() .
Знак последнего
слагаемого выбран с учётом того, что на
.
Знак последнего
слагаемого выбран с учётом того, что на
![]()
![]() .
Если в полной границе области V
присутствует цилиндрическая составляющая
.
Если в полной границе области V
присутствует цилиндрическая составляющая
![]() ,
то
,
то
![]() ,
поэтому
окончательно
,
поэтому
окончательно
 .
Совершенно аналогично доказываются
формулы для двух других слагаемых.
Формула Остроградского доказана.
.
Совершенно аналогично доказываются
формулы для двух других слагаемых.
Формула Остроградского доказана.
Применим формулу
Остроградского для решения задачи,
рассмотренной в предыдущем разделе:
найти поток векторного поля ![]() через полную внешнюю поверхность тела,
ограниченного поверхностями
через полную внешнюю поверхность тела,
ограниченного поверхностями ![]() :
:
![]() ,
,
![]()

![]() .
Естественно,
ответ получился тот же; но этот способ
вычисления оказался самым простым.
.
Естественно,
ответ получился тот же; но этот способ
вычисления оказался самым простым.
1 7.3.5.
Инвариантное определение дивергенции.
В разделе 17.2.2.1.
Дивергенция векторного поля
мы определили дивергенцию как выражение
в определённой системе координат :
7.3.5.
Инвариантное определение дивергенции.
В разделе 17.2.2.1.
Дивергенция векторного поля
мы определили дивергенцию как выражение
в определённой системе координат :
![]() .
Теорема Остроградского позволяет понять
смысл дивергенции поля в точке М
как объективного атрибута векторного
поля без использования координатной
системы. Пусть
.
Теорема Остроградского позволяет понять
смысл дивергенции поля в точке М
как объективного атрибута векторного
поля без использования координатной
системы. Пусть
![]() - замкнутая поверхность, окружающая
точку М,
V
- тело, заключенное внутри
- замкнутая поверхность, окружающая
точку М,
V
- тело, заключенное внутри
![]() ,
,
![]() - вектор единичной внешней нормали к
- вектор единичной внешней нормали к
![]() .
Тогда
.
Тогда
![]() .
По теореме о среднем для тройного
интеграла существует точка
.
По теореме о среднем для тройного
интеграла существует точка ![]() такая, что
такая, что
![]() .
Следовательно,
.
Следовательно,
![]() .
Отношение значения некоторой физической
величины к объёму принято называть
средней плотностью этой величины в
объёме; если объём стягивается к точке
М,
предел средней плотности называется
локальным значением плотности в точке
М.
Таким образом, мы можем трактовать
.
Отношение значения некоторой физической
величины к объёму принято называть
средней плотностью этой величины в
объёме; если объём стягивается к точке
М,
предел средней плотности называется
локальным значением плотности в точке
М.
Таким образом, мы можем трактовать
![]() как среднюю плотность потока в объёме
V.
Будем теперь стягивать
как среднюю плотность потока в объёме
V.
Будем теперь стягивать
![]() к точке М,
при этом и V
стягивается к точке М;
к точке М,
при этом и V
стягивается к точке М;
![]() ,
и, вследствие непрерывности
,
и, вследствие непрерывности
![]() ,
,
![]() .
Поэтому
.
Поэтому
 будет равна
плотности
потока в
точке М,
и так как плотность потока определяется
независимо от выбора какой-либо системы
координат, то дивергенция векторного
поля инвариантна относительно выбора
координатной системы.
будет равна
плотности
потока в
точке М,
и так как плотность потока определяется
независимо от выбора какой-либо системы
координат, то дивергенция векторного
поля инвариантна относительно выбора
координатной системы.
Используем теперь
гидродинамическую интерпретацию поля
для выяснения физического смысла
дивергенции. Пусть
![]() (M)
- стационарное поле скоростей несжимаемой
жидкости. В каком случае поток
(M)
- стационарное поле скоростей несжимаемой
жидкости. В каком случае поток
![]() через
замкнутую поверхность
через
замкнутую поверхность
![]() может быть отличен от нуля, т.е. в каком
случае из V
вытекает
больше жидкости, чем втекает (при П>0)
или наоборот (при П<0)? Ясно, что П>0
может быть только в том случае, если в
V
появляется дополнительная жидкость,
т.е. в V
имеются
источники поля. П<0 может быть только
в том случае, если в V
исчезает часть жидкости, т.е. в V
имеются
стоки поля. Поэтому
может быть отличен от нуля, т.е. в каком
случае из V
вытекает
больше жидкости, чем втекает (при П>0)
или наоборот (при П<0)? Ясно, что П>0
может быть только в том случае, если в
V
появляется дополнительная жидкость,
т.е. в V
имеются
источники поля. П<0 может быть только
в том случае, если в V
исчезает часть жидкости, т.е. в V
имеются
стоки поля. Поэтому
![]() как плотность
потока в точке М
определяет силу источника (при
как плотность
потока в точке М
определяет силу источника (при
![]() >0)
или стока (при
>0)
или стока (при
![]() <0)
в точке М.
<0)
в точке М.
По аналогии с полем
скоростей жидкости считают, что
дивергенция определяет силу источников
и стоков поля в любом поле
![]() (M).
(M).
