
- •16. Кратные, криволинейные, поверхностные интегралы.
- •16.1. Двойной интеграл.
- •16.1.3. Свойства двойного интеграла.
- •16.1.5. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •16.1.6. Задачи на двойной интеграл.
- •16.1.7. Приложения двойного интеграла.
- •16.2. Тройной интеграл.
- •16.2.2.3. Интеграл от единичной функции по области V равен объёму этой области: .
- •16.2.5. Замена переменных в тройном интеграле.
- •14.3. Несобственные кратные интегралы.
- •16.3. Криволинейные интегралы.
- •16.3.2. Криволинейный интеграл первого рода (по длине дуги).
- •16.3.2.4. Механические приложения криволинейного интеграла 1-го рода.
- •16.3.3. Криволинейный интеграл второго рода (по координатам).
- •16.3.3.4. Формула Грина.
- •16.3.3.6. Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути.
- •16.4. Поверхностные интегралы.
- •16.4.3. Поверхностный интеграл первого рода (по площади поверхности).
- •16.4.3.3. Вычисление поверхностного интеграла первого рода.
- •6.4.3.4. Механические и физические приложения поверхностного интеграла 1-го рода.
- •16.4. Поверхностные интегралы.
- •16.4.4. Поверхностный интеграл второго рода (по координатам).
- •17. Теория поля.
- •17.1. Скалярное поле.
- •17.1.2. Частные случаи скалярных полей.
- •17.2. Векторное поле.
- •17.2.2. Дифференциальные характеристики векторного поля.
- •17.2.2.1. Дивергенция векторного поля.
- •17.2.3. Частные случаи векторных полей.
- •17.3.Поток векторного поля через поверхность.
16.4.3. Поверхностный интеграл первого рода (по площади поверхности).
16.4.3.1. Определение
поверхностного интеграла первого рода.
Пусть в
пространстве переменных x,y,z
задана
кусочно-гладкая поверхность ![]() ,
на которой определена функция
f(x,y,z).
Разобьём
поверхность на
,
на которой определена функция
f(x,y,z).
Разобьём
поверхность на ![]() частей
частей ![]() ,
на каждой из частей
,
на каждой из частей ![]() выберем произвольную точку
выберем произвольную точку ![]() ,
найдём
,
найдём ![]() и площадь части
и площадь части ![]() (которую будем обозначать тем же символом
(которую будем обозначать тем же символом
![]() ),
и составим интегральную сумму
),
и составим интегральную сумму ![]() .
Если существует предел последовательности
интегральных сумм при
.
Если существует предел последовательности
интегральных сумм при ![]() ,
не зависящий ни от способа разбиения
поверхности
,
не зависящий ни от способа разбиения
поверхности ![]() на части
на части ![]() ,
ни от выбора точек
,
ни от выбора точек ![]() ,
то функция f(x,y,z)
называется интегрируемой по поверхности
,
то функция f(x,y,z)
называется интегрируемой по поверхности
![]() ,
а значение этого предела называется
поверхностным интегралом первого рода,
или поверхностным интегралом по площади
поверхности, и обозначается
,
а значение этого предела называется
поверхностным интегралом первого рода,
или поверхностным интегралом по площади
поверхности, и обозначается ![]() .
.
Теорема
существования.
Если функция f(x,y,z)
непрерывна на поверхности ![]() ,
то она интегрируема по этой поверхности.
,
то она интегрируема по этой поверхности.
16.4.3.2. Свойства поверхностного интеграла первого рода. Для этого интеграла имеют место основные шесть свойств, справедливых для определённого, двойного, тройного интеграла, от линейности до теоремы о среднем. Сформулировать и доказать их самостоятельно. Седьмое, персональное, свойство - независимость поверхностного интеграла первого рода от выбора стороны поверхности.
16.4.3.3. Вычисление поверхностного интеграла первого рода.
16.4.3.3.1. Определение
единичного вектора нормали к поверхности.
Выражения для элемента площади
поверхности. Предположим,
что поверхность ![]() задаётся неявным уравнением
задаётся неявным уравнением ![]() (
(![]() - непрерывно дифференцируемая функция)
и взаимно однозначно проецируется в
область
- непрерывно дифференцируемая функция)
и взаимно однозначно проецируется в
область ![]() на плоскости
Оху. Из
теории функций нескольких переменных
известно, что градиент функции ортогонален
поверхности уровня этой функции,
проходящей через точку, в которой найден
градиент. Рассматривая уравнение
на плоскости
Оху. Из
теории функций нескольких переменных
известно, что градиент функции ортогонален
поверхности уровня этой функции,
проходящей через точку, в которой найден
градиент. Рассматривая уравнение ![]() как уравнение поверхности уровня функции
трёх переменных
как уравнение поверхности уровня функции
трёх переменных ![]() ,
получаем, что в каждой точке поверхности
,
получаем, что в каждой точке поверхности
![]()
![]() ортогонален
ортогонален ![]() ,
т.е. является нормальным к
,
т.е. является нормальным к ![]() вектором. Чтобы получить единичный
нормальный вектор, достаточно просто
пронормировать
вектором. Чтобы получить единичный
нормальный вектор, достаточно просто
пронормировать ![]() :
:
![]() ,
где знак перед дробью соответствует
возможности выбора двух возможных
взаимно противоположных направлений
нормали. В координатной форме
,
где знак перед дробью соответствует
возможности выбора двух возможных
взаимно противоположных направлений
нормали. В координатной форме 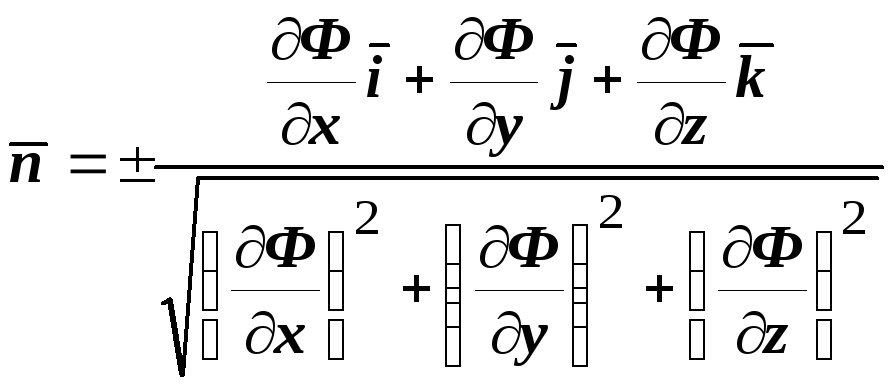 ,
где
,
где ![]() - базисные орты. Если сравнить это
выражение с представлением градиента
через направляющие косинусы:
- базисные орты. Если сравнить это
выражение с представлением градиента
через направляющие косинусы: ![]() ,
то
,
то 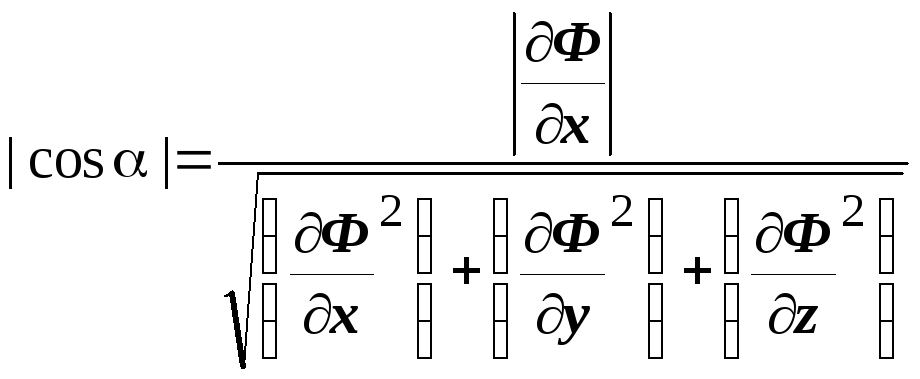 ,
,
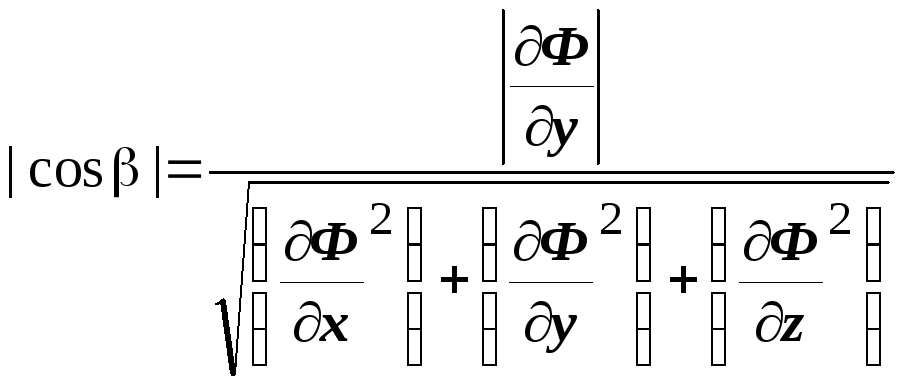 ,
,
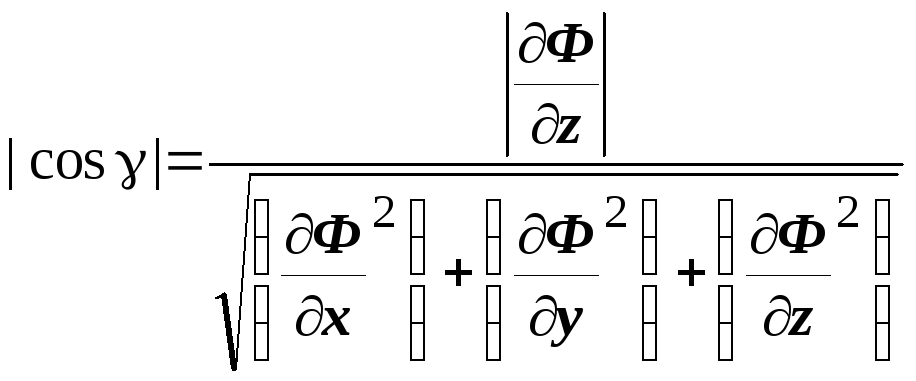 .
Теперь мы можем выразить элемент площади
поверхности через элемент площади в
каждой координатной плоскости:
.
Теперь мы можем выразить элемент площади
поверхности через элемент площади в
каждой координатной плоскости:  ,
,
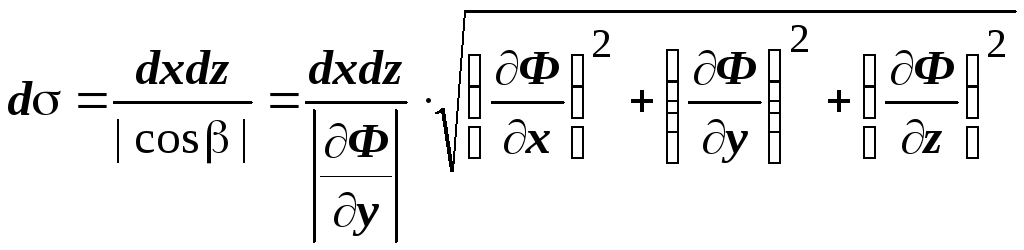 ,
,
 .
В частном случае задания уравнения
поверхности в явном виде
.
В частном случае задания уравнения
поверхности в явном виде ![]() получим
получим ![]() ,
т.е.
,
т.е. ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
поэтому
,
поэтому ![]() ,
,
![]() ,
,
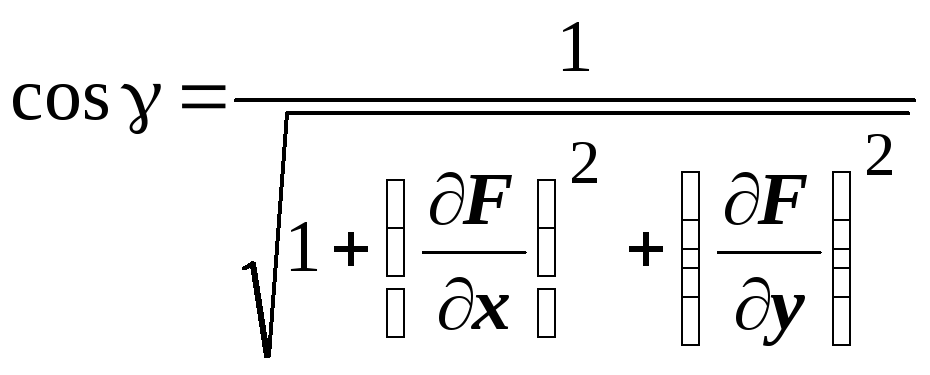 ,
и
,
и ![]() .
Мы уже пользовались этой формулой при
вычислении площади поверхности с помощью
двойного интеграла.
.
Мы уже пользовались этой формулой при
вычислении площади поверхности с помощью
двойного интеграла.
 16.4.3.3.2.
Выражение поверхностного интеграла
через двойной интеграл по проекции
поверхности на координатную плоскость.Пусть
поверхность
16.4.3.3.2.
Выражение поверхностного интеграла
через двойной интеграл по проекции
поверхности на координатную плоскость.Пусть
поверхность
![]() взаимно однозначно проецируется в
область
взаимно однозначно проецируется в
область ![]() на плоскости
Оху. Будем
считать, что поверхность задана уравнением
на плоскости
Оху. Будем
считать, что поверхность задана уравнением
![]() ,
,
![]() .
В интегральной сумме
.
В интегральной сумме ![]() выразим площадь
выразим площадь ![]() через двойной интеграл по её проекции
через двойной интеграл по её проекции
![]() на плоскость Оху:
на плоскость Оху:
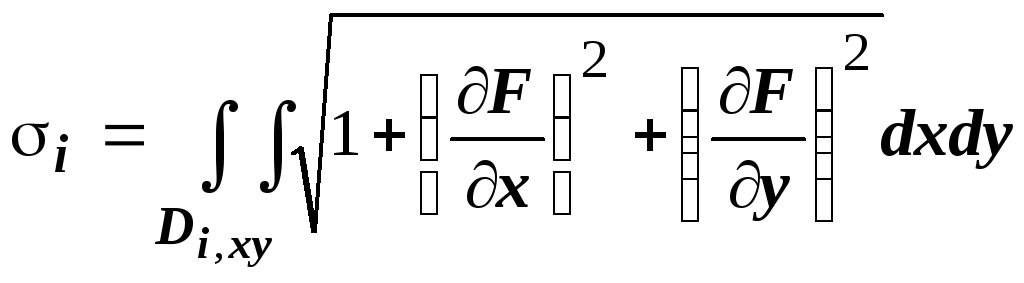 .
Применим к этому интегралу теорему о
среднем: существует точка
.
Применим к этому интегралу теорему о
среднем: существует точка ![]() такая, что
такая, что ![]() .
Значение подынтегральной функции
.
Значение подынтегральной функции ![]() будем вычислять в точке
будем вычислять в точке ![]() ,
такой, что
,
такой, что ![]() .
Тогда
.
Тогда ![]() .
.
Слева
стоит интегральная сумма для поверхностного
интеграла, справа - для двойного; переход
к пределу при ![]() (при этом и
(при этом и ![]() )
даёт
)
даёт
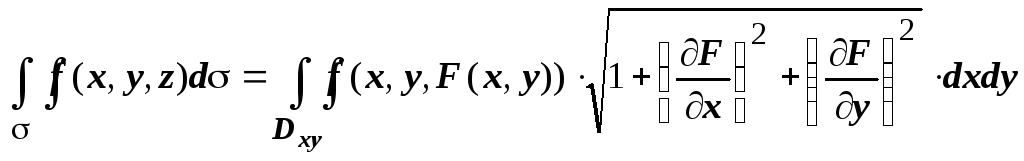 .
.
Эта формула и применяется для вычисления поверхностных интегралов. Естественно, в каждой задаче надо выбирать, на какую из координатных плоскостей предпочтительней проецировать поверхность; если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно.
Примеры.
1. Найти ![]() ,
где
- часть цилиндра
x2 +
z2
= 2x,
вырезаемая гиперболоидом x2
- y2
+ z2
= 1 и
плоскостью z
= 0 (z
> 0).
,
где
- часть цилиндра
x2 +
z2
= 2x,
вырезаемая гиперболоидом x2
- y2
+ z2
= 1 и
плоскостью z
= 0 (z
> 0).
Решение: Найдем проекцию поверхности на плоскость OXY. Исключим из уравнений цилиндра и гиперболоида переменную z:
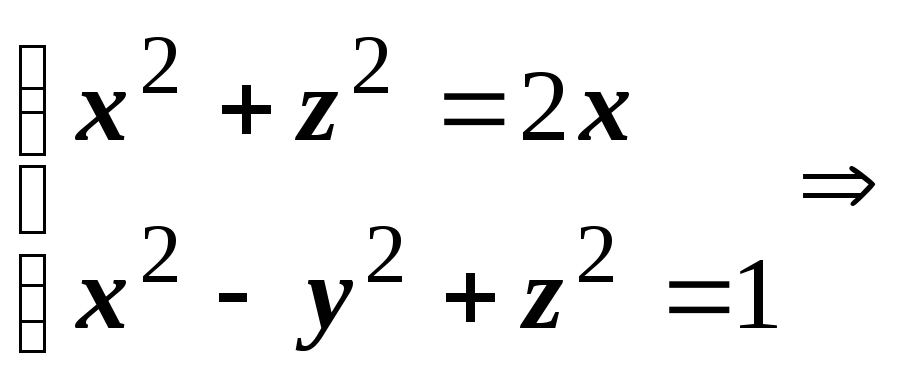 2x
= y2+1
- уравнение проекции линии пересечения
двух поверхностей на OXY.
П
2x
= y2+1
- уравнение проекции линии пересечения
двух поверхностей на OXY.
П
 олагая
в уравнении цилиндраz
= 0, получим уравнение линии пересечения
цилиндра и плоскости OXY.
Таким образом, поверхность
проецируется в область D,
ограниченную параболой x
=
олагая
в уравнении цилиндраz
= 0, получим уравнение линии пересечения
цилиндра и плоскости OXY.
Таким образом, поверхность
проецируется в область D,
ограниченную параболой x
=![]() (y2+1)
и прямой x=2.
Часть цилиндра, удовлетворяющая условию
z>0,
задается уравнением z
=
(y2+1)
и прямой x=2.
Часть цилиндра, удовлетворяющая условию
z>0,
задается уравнением z
= ![]() .
Тогда
.
Тогда ![]()
![]() =
=
![]() =
=![]() .
Таким образом,
.
Таким образом, ![]()
![]()
![]() .
.
 2.
Найти
2.
Найти![]() ,
где
- полная поверхность цилиндра x2+y2
= 1, 0 ≤
z
≤
1.
,
где
- полная поверхность цилиндра x2+y2
= 1, 0 ≤
z
≤
1.
Решение:
Искомый интеграл равен сумме трех
интегралов: по нижнему и верхнему
основаниям 1
и 2
и боковой поверхности (рис.18). Так как
на нижнем основании z=0, то
![]() =0.
Для верхнего основания2
имеем z(x,y)=1,
=0.
Для верхнего основания2
имеем z(x,y)=1,
![]() =
=![]() =0,
поэтому поверхностный интеграл по2
совпадает с двойным интегралом от
функции z(x,y)|xy|
= |xy|,
взятым по кругу D
={x2+
y2<1}:
=0,
поэтому поверхностный интеграл по2
совпадает с двойным интегралом от
функции z(x,y)|xy|
= |xy|,
взятым по кругу D
={x2+
y2<1}:
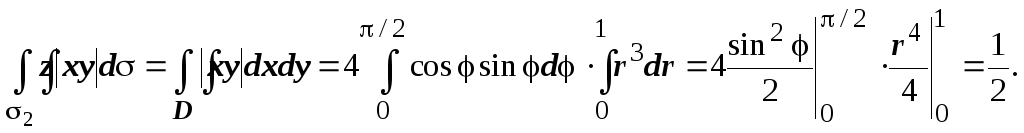
Найдем интеграл по боковой поверхности. Она состоит из двух частей: 3 и 4 , симметричных относительно плоскости OYZ. Так как функция z|xy| - четная по x, то интегралы по 3 и 4 равны.
Проекция 3
на плоскость
OYZ
- прямоугольник D:{-1
≤
у
≤
1, 0 ≤
z
≤1}.
Уравнение 3
: х=![]()
![]() Отсюда:
Отсюда: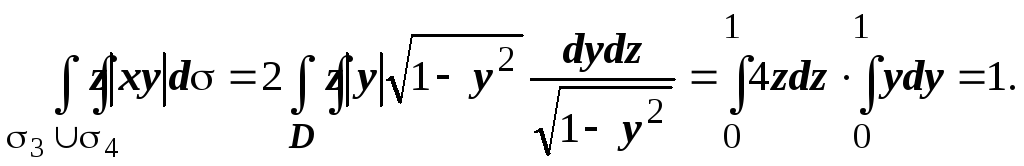
Окончательно
получаем:
![]()
3. Найти
![]() ,
где
- сфера x2
+ y2
+ z2
= R2.
,
где
- сфера x2
+ y2
+ z2
= R2.
Решение:
Использование соображений симметрии
позволяет иногда существенно упростить
вычисление интегралов. Очевидно, что
для сферы
![]() .
Тогда
.
Тогда
![]()
