16. Кратные, криволинейные, поверхностные интегралы.

16.1. Двойной интеграл.

16.1.1. Определение двойного интеграла. Теорема существования двойного интеграла. Пусть на плоскости Oxy задана ограниченная замкнутая область D с кусочно-гладкой границей, и пусть на области D определена функция .

Разобьём область D произвольным образом на подобластей (не имеющих общих внутренних точек). Символом будем обозначать площадь области ; символом здесь и дальше будет обозначаться наибольшее расстояние между двумя точками, принадлежащими области D:

;

символом обозначим наибольший из диаметров областей : .

В каждой из подобластей выберем произвольную точку , вычислим в этой точке значение функции , и составим интегральную сумму .

Если существует предел последовательности интегральных сумм при , не зависящий ни от способа разбиения области D на подобласти , ни от выбора точек , то функция называется интегрируемой по области D, а значение этого предела называется двойным интегралом от функции по области D и обозначается .

Если расписать значение через координаты точки , и представить как , получим другое обозначение двойного интеграла: . Итак, кратко, .

Теорема существования двойного интеграла. Если подынтегральная функция непрерывна на области D, то она интегрируема по этой области.

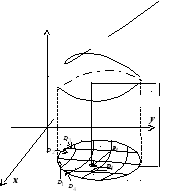
16.1.2. Геометрический смысл двойного интеграла. Геометрический смысл каждого слагаемого интегральной суммы: если , то - объём прямого цилиндра с основанием высоты ; вся интегральная сумма - сумма объёмов таких цилиндров, т.е. объём некоторого ступенчатого тела (высота ступеньки, расположенной над подобластью , равна ). Когда , это ступенчатое тело становится всё ближе к изображенному на рисунке телу, ограниченному снизу областью , сверху - поверхностью , с цилиндрической боковой поверхностью, направляющей которой является граница области , а образующие параллельны оси . Двойной интеграл равен объёму этого тела.

16. 16.1.3. Свойства двойного интеграла.

17. 16.1.3.1. Линейность. Если функции , интегрируемы по области , то их линейная комбинация тоже интегрируема по области , и .

Док-во. Для интегральных сумм справедливо равенство . Переходя к пределу при и пользуясь свойствами пределов, рассмотренными в разделе 4.4.6. Арифметические действия с пределами (конкретно, свойствами 4.4.10.1 и 4.4.10.2), получим требуемое равенство.

16.1.3.2. А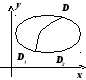ддитивность. Если область является объединением двух областей и , не имеющих общих внутренних точек, то .

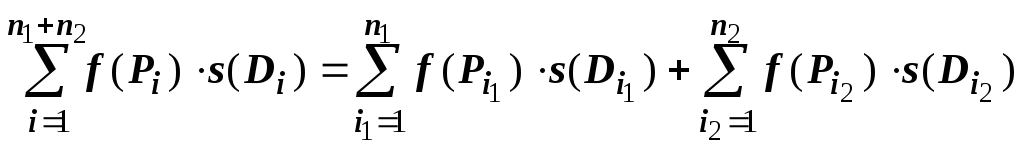Док-во. Пусть область разбита на подобласти , область разбита на подобласти . Тогда объединение этих разбиений даст разбиение области : на подобластей. Интегральная сумма по области равна сумме сумм по областям и : . Как и в предыдущем случае, переходя к пределу при , получим требуемое равенство.

3. Интеграл от единичной функции по области равен площади этой области: .

Док-во: Для любого разбиения , т.е. не зависит ни от разбиения, ни от выбора точек . Предел постоянной равен этой постоянной, поэтому .

16.1.3.4. Интегрирование неравенств. Если в любой точке выполняется неравенство , и функции интегрируемы по области , то .

Док-во. В любой точке выполняется неравенство , поэтому . По теореме о переходе к пределу в неравенствах отсюда следует требуемое утверждение.

5. Теоремы об оценке интеграла.

16.1.3.5.1. Если функция интегрируема по области , и для выполняется , то .

Док-во. (цифрами над знаками импликации обозначены номера применяемых ранее доказанных свойств).

16.1.3.5.2. Если функция интегрируема по области , то .

Док-во. Эти неравенства непосредственно следуют из того, что и свойства 16.1.3.4. Интегрирование неравенств.

16.1.3.6. Теорема о среднем. Если функция непрерывна на области , то существует точка , такая что .

Док-во. Непрерывная на ограниченной замкнутой области функция принимает в некоторых точках этой области своё минимальное и максимальное значения. Так как , то , или . Непрерывная функция принимает, кроме того, любое значение, заключённое между и , в частности, значение . Следовательно, , откуда и следует доказываемое утверждение.

3. Вычисление двойного интеграла. Двукратный (повторный) интеграл.

1. Определение простой (правильной) области. Область на плоскости Oxy будем называть простой (правильной) в направлении оси Oy, если любая прямая, проходящая через внутреннюю точку области и параллельная оси Oy, пересекает границу в двух точках.

Аналогично определяется область, простая (правильная) в направлении оси Ox: любая прямая, проходящая через внутреннюю точку области и параллельная оси Oх, пересекает границу в двух точках.

Область, правильную (простую) в направлении обеих осей, будем называть правильной.

О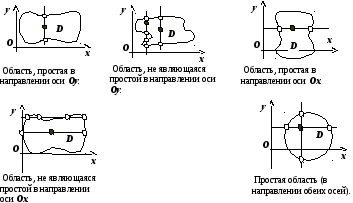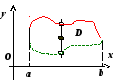граниченную замкнутую область, правильную в направлении оси Oy, можно описать неравенствами 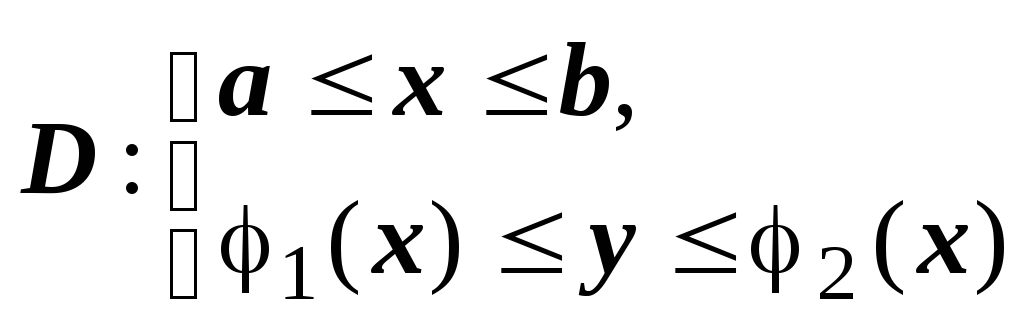. Числа и существуют вследствие ограниченности области , функция образована нижними точками пересечения прямой при с границей области , функция - верхними точками пересечения этой прямой с границей области :

Аналогичным образом область , ограниченную, замкнутую и правильную в направлении оси Oх, можно описать неравенствами . Функция образована левыми точками пересечения прямой при с границей области , функция - правыми точками пересечения этой прямой с границей области .

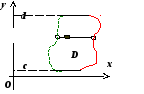Для правильной области (т.е. области, правильной в направлении обеих осей) существуют оба способа представления: и 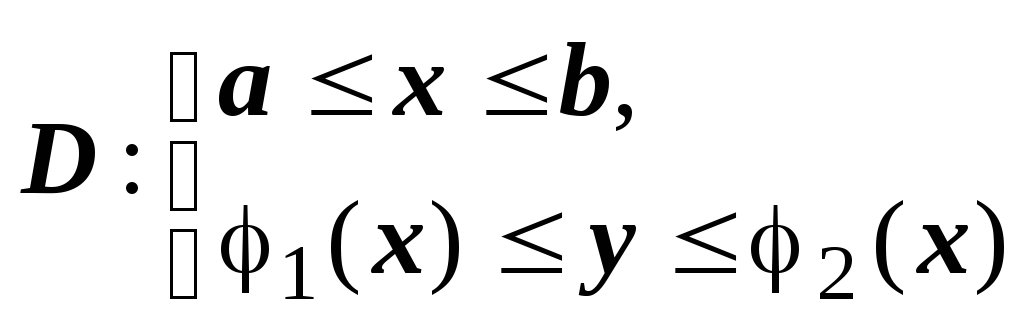, и .

2. Двукратный (повторный) интеграл. Пусть - область, простая в направлении оси Oy. Рассмотрим выражение . Эта конструкция определяется через два обычных определённых интеграла. После интегрирования по у во внутреннем интеграле (переменная х при этом рассматривается как постоянная) и подстановки по у в пределах от до получается функция, зависящая только от х, которая интегрируется в пределах от a до b. В дальнейшем мы будем обычно записывать этот объект без внутренних скобок:

.

Можно показать, что двукратный интеграл обладает всеми свойствами двойного интеграла:

Свойства линейности и интегрирования неравенств следуют из этих свойств определённого интеграла; интеграл от единичной функции даёт площадь области: ;

теоремы об оценке и о среднем следуют из перечисленных свойств. Единственное свойство, с которым придётся повозиться - это свойство аддитивности. Мы докажем его в простой, но достаточной для нас форме: если область разбита на две подобласти и прямой, параллельной одной из координатных осей, то двукратный интеграл по области равен сумме интегралов по и : .

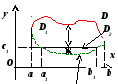Первый случай: прямая параллельна оси Oy. Тогда (аддитивность внешнего интеграла) .

Второй случай: прямая параллельна оси Oх. Воспользуемся сначала аддитивностью внешнего интеграла:

(теперь применим свойство аддитивности для внутреннего интеграла в среднем слагаемом) = (применяем свойство линейности для внешнего интеграла в среднем слагаемом и перегруппировываем сумму)=

(первая фигурная скобка даёт повторный интеграл по , второй - по ) .

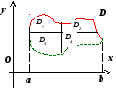Понятно, что воэможны различные случаи взаимного расположения прямых, , и функций , , но логика доказательства во всех случаях такая же.

Обобщим доказанное свойство. Пусть прямая разбивает область на две подобласти и . Проведём ещё одну прямую, параллельную какой-либо координатной оси. Пусть эта прямая разбивает на и; - на и . По доказанному, , , поэтому . Продолжая рассуждать также, убеждаемся в справедливости следующего утверждения: если область с помощью прямых, параллельных координатным осям, разбита на подобласти , то .

3. Теорема о переходе от двойного интеграла к повторному. Пусть - простая в направлении оси Oy область. Тогда двойной интеграл от непрерывной функции по области равна повторному интегралу от той же функции по области : .

Док-во. Разобьём область с помощью прямых, параллельных координатным осям, на подобласти . По доказанному выше, 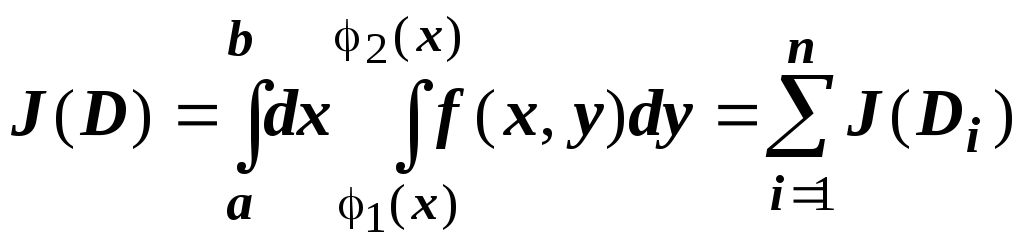. К каждому из итегралов применим теорему о среднем: в любой области найдётся точка такая, что . Следовательно, . В последнем равенстве справа стоит интегральная сумма для двойного интеграла . Будем мельчить разбиение области так, чтобы . Вследствие непрерывности функции по теореме существования интегральная сумма при этом стремится к двойному интегралу , т.е. в пределе получим , что и требовалось доказать.

Если область правильная в направлении оси Oх, то аналогично доказывается формула . Если правильна в направлении обеих осей, то для вычисления двойного интеграла можно применять любую из эти формул: .

Если область не является правильной, её разбивают на правильные подобласти.