2523

(5.3, б), (5.4, а, б), (5.5, а, б) и (5.10, б) для чисел несправедливы; кроме того, понятие «инверсия» для чисел вообще не определено. Выражения типа 2x и х2 в алгебре логики не встречаются в силу правила повторения.

Сравнивая левые и правые уравнения, следует обратить внимание на содержащийся в них дуализм: если в каком-нибудь тождестве поменять местами конъюнкцию с дизъюнкцией и 0 с 1, то при этом также получится тождество.

С помощью выражений (5.9)-(5.11) можно вычислить результаты конъюнкции и дизъюнкции для всех возможных значений переменных х1 и х2. В табл. 5.1 и 5.2 представлены соответственно функции конъюнкции и дизъюнкции.

Таблица 5.1

Из табл. 5.1 следует, что у только тогда равен 1, когда x1 x2 равны 1. На этом основании операция конъюнкции называется также функцией И. При дизъюнкции двух переменных у равен 1 тогда, когда х1 или х2 равны 1. Поэтому операцию дизъюнкции называют также функцией ИЛИ. Обе эти функции можно распространить на сколь угодно большое число переменных. Возникает вопрос: как можно представить логические функции с помощью электрических переключающих схем, обладающих двумя устойчивыми состояниями, различающимися величинами электрического напряжения? Этим состояниям можно поставить в соответствие логические состояния 1 и 0. При этом система обозначений: высокий уровень напряжения = 1 и низкий = 0 называется позитивной логикой. Но возможна также и обратная система обозначений: высокий = 0 и низкий = 1, которая называется негативной логикой.

Основные логические функции могут быть реализованы с помощью соответствующих электронных схем. Эти схемы имеют один или несколько

61

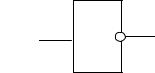
входов и один выход. Как правило, они называются логическими элементами. Уровень выходного напряжения определяется уровнями напряжения на входах и характером логической функции. Для реализации одной и той же логической функции существует большое число различных электронных схем.

Поэтому с целью упрощения документации были введены символы, которые обозначают лишь только логическую функцию и не раскрывают внутреннее строение схемы. Эти обозначения представлены на рис. 5.1 – 5.3.

Рис. 5.1. Схема И

Рис. 5.3. Схема НЕ

В цифровой технике входные и выходные сигналы обычно характеризуются не их физическими величинами - напряжениями U1, U2 … и т.д., а непосредственно значениями логических переменных х1, х2....

5.1.2. Составление логических функций

В цифровой технике задача, как правило, формулируется в форме таблицы переключений, которая называется также таблицей истинности. Прежде всего, требуется найти такую логическую функцию, которая соответствовала бы этой таблице. На следующем этапе эту функцию преобразуют в простейшую форму, которую потом реализуют с помощью соответствующей комбинации базовых логических схем. Логические функции записывают, как правило, в дизъюнктивной нормальной форме. При этом поступают следующим образом:

1) в таблице истинности выделяют строки, в которых выходная переменная у имеет значение 1;

62

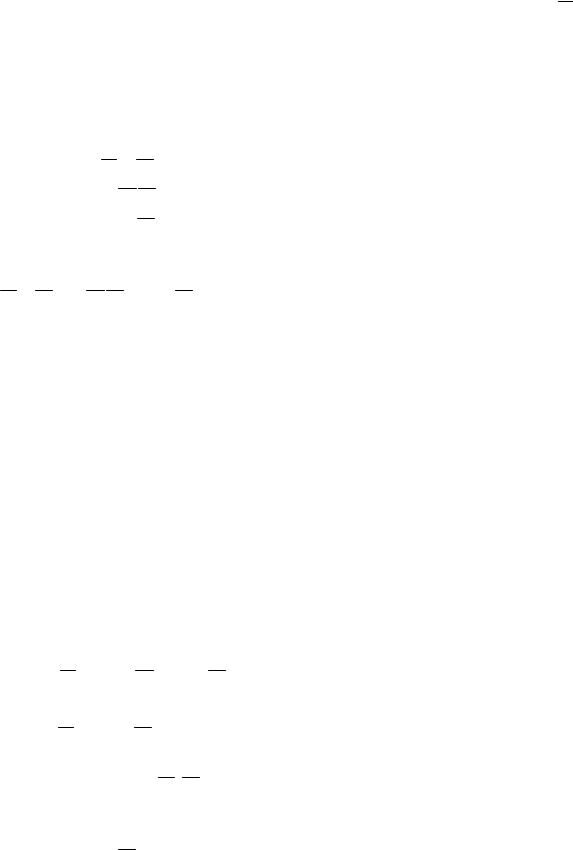
2) для каждой такой строки составляют конъюнкцию всех входных переменных, причем записывают сомножитель хi , если рассматриваемая

переменная принимает значение 1, в противном случае записывают xi . Таким образом, составляется столько произведений, сколько имеется строк с у=1;

3) наконец, записывая логическую сумму всех найденных произведений, получают искомою функцию.

Рассмотрим этот способ на примере таблицы истинности 5.3. В строчках 3, 5 и 7 переменная у=1. Прежде всего, следует составить конъюнкцию для этих строк.

Строка 3: K3 x1x2x3 .

Строка 5: K5 x1x2x3 .

Строка 7: K7 x1x2x3 .

Искомая функция записывается в виде логической суммы произведений: y=K3+K5+K7,

y=x1x2x3 +x1x2x3 +x1x2x3 .

Эта запись является дизъюнктивной нормальной формой рассматриваемой логической функции. В отечественной литературе такая запись называется также совершенной дизъюнктивной нормальной формой (СДНФ). Для ее упрощения применим выражение (5.3), после чего получим

y x1x2 x1(x2 x2) x3 .

Дальнейшее упрощение возможно, если учесть выражения (5.6, б) и (5.9, а):

y (x1x2 x1)x3 .

Согласно формуле (5.3, б),

y (x1 x2)(x1 x1)x3 .

Еще раз применяя тождества (5.6, б) и (5.9, а), запишем простой конечный результат:

y (x1 x2)x3 .

Если в таблице истинности в столбце выходной переменной у стоит больше единиц, чем нулей, требуется составить много произведений. В этом случае, с

63

целью упрощения вместо у рассматривают инвертированную выходную переменную y. Для этой переменной единиц уже имеется меньше, чем нулей.

Затем для инвертированной переменной y вычисляют логическую функцию, в которую входит уже меньшее число произведений, после чего ее упрощают. Найденную таким образом функцию инвертируют, получая при этом искомое логическое выражение для у. Для этого заменяют операцию (+) на ( ) и наоборот, а все переменные и константы (каждую в отдельности) инвертируют.

5.1.3. Представление заданной функции в базисах И-НЕ, ИЛИ-НЕ

Совокупность элементарных логических функций, с помощью которых можно записать любую функцию Y(νi), называется функционально полной системой функций или базисом.

Для представления любой функции Y(νi) в совершенной дизъюнктивной нормальной форме (СДНФ) и совершенной конъюнктивной нормальной форме (СКНФ) достаточно использовать только функции И, ИЛИ и НЕ, т.е. совокупность этих функций является базисом. Базисом также являются функции И-НЕ и ИЛИ-НЕ. Для получения логической функции следует представить её в минимальной нормальной форме (МНФ) т.е. в таком виде когда в логическом выражении, определяющем функцию Y(νi). Последовательно выполняются не более чем две операции из совокупности операций И, ИЛИ, НЕ, И-НЕ,ИЛИ-НЕ.

Для представления полученной логической функции в требуемом базисе наиболее удобно использовать закон двойного отрицания и закон двойственности, который обладает замечательным свойством: при преобразовании любого логического выражения на основании закона двойственности ни число первичных термов, ни общее число операций дизъюнкции и конъюнкции, входящих в исходное логическое выражение, не изменяется.

Пусть получена МДНФ некоторой функции, напримерY(νi) полученная в предыдущем параграфе Y=x1x3+x2x3 . Используя закон двойного отрицания и закон двойственности, получаем

Y x1x3 x2x3 x1x3 x2x3 .

Это соотношение и дает МНФ функции в базисе И-НЕ, так как для ее реализации требуются только операции И-НЕ. Запишем МНФ в базисе И-НЕ функции трех переменных, МДНФ которой была найдена. Получение минимальной конъюнктивной нормальной формы (МКНФ) функции легко сводится к получению МДНФ инверсной функции и преобразованию ее с помощью закона двойственности. В базисе ИЛИ-НЕ МНФ функция может быть получена непосредственно из МКНФ с помощью закона двойного отрицания и закона двойственности. Для этого сначала записываем СКНФ, составляя логические произведения логических сумм инвертированных переменных для значений функции, равных 0. После упрощения и получения МНФ применяем

64

двойное отрицание и закон двойственности и получаем требуемую функцию базисе ИЛИ-НЕ.

5.1.4.Минимизация логических функций

Вряде случаев запись логической функции в виде СДНФ или СКНФ не является самой простой и логическое выражение можно упростить, не нарушая значения функции.

Методы такого упрощения функции называются способами минимизации. В результате минимизации логические функции могут быть представлены в ДНФ или в КНФ с минимальным числом членов и с минимальным числом аргументов

вкаждом члене.

После проведения всех преобразований получают функцию, не имеющую избыточных членов и не подающуюся дальнейшей минимизации. Эту форму записи функции называют тупиковой. Функция может иметь несколько тупиковых форм. При минимизации используют алгебраические и графические методы. Алгебраические методы в процессе минимизации используют аксиомы и правила алгебры логики. Они требуют достаточно большого опыта от разработчика.

Графические методы формализуют процедуру минимизации. Эти методы используют таблицы (карты) Вейча или Карно, различающиеся оформлением и размещением ячеек. Остановим свой выбор на картах Карно.

При составлении карты Карно исходной информацией служит таблица истинности логической функции. В картах Карно каждому набору значений аргументов по строкам и столбцам соответствует ячейка, расположенная на их пересечении. Она заполняется единицей, если на соответствующем наборе аргументов функция принимает единичное значение, или нулем при нулевом значении функции. Ячейки, отмеченные единицей, соответствуют минтермам, а нулем - макстермам канонической формы (СДНФ или СКНФ).

Карты Карно применяют для минимизации функций с числом аргументов от двух до шести.

На рис. 4.28. показана карта Карно для функции от двух переменных. Вдоль верхней границы поставлены возможные значения переменной X1, вдоль левой боковой грани - возможные значения переменной X2.

Рис. 5.4. Карта Карно для логической функции от двух аргументов

65

Карта содержит четыре клетки. В каждой клетке изображают один из возможных минтермов

X2 X1 , X2 X1, X2 X1 , X2 X1.

Если значение логической функции в N-ой строке таблицы истинности (N – порядковый номер кодовой комбинации аргументов) равно 1, то в ячейке с номером N записывается 1, в противном случае – 0.

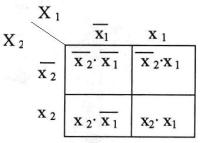
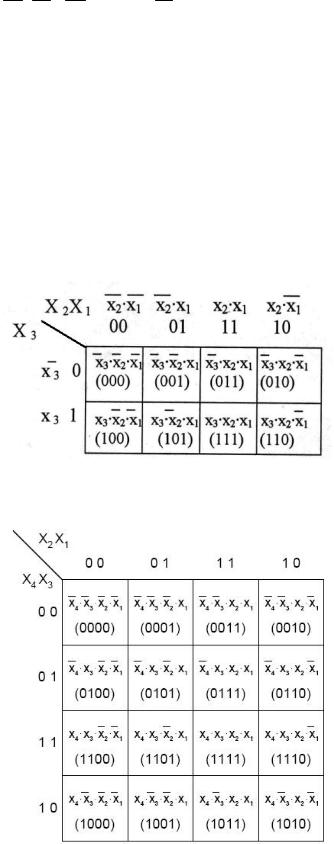
Карты Карно для функций трех и четырех переменных показаны на рис. 5.6 и 5.7 соответственно.

Метод минимизации с помощью карт Карно состоит из следующих операций:

-заполнение карты Карно;

-объединение соседних клеток в группы (импликанты);

-исключение избыточных минтермов или макстермов и избыточных переменных.

Рис. 5.5. Карта Карно для логической функции от трех переменных

Рис. 5.6. Карта Карно для логической функции от четырех переменных

66

Объединение соседних клеток в области осуществляется по следующим правилам:

выделяются группы соседних 2g клеток, содержащих или «1», или «0». Степень 2 – g обозначим как степень группирования клеток. Некоторые клетки могут входить в другие группы соседних клеток (группы пересекаются). При группировании клеток карты следует стремиться, чтобы число групп было минимальным, т.к. при этом будет минимальное число членов ДНФ, а каждая группа содержала наибольшее количество клеток (наибольшую степень группирования). При этом число аргументов в членах ДНФ будет минимальным;

соседними считаются также клетки первой и последней строк, а также клетки первого и последнего столбцов.

для клеток с «1» производится запись минимизированного алгебраического

L

выражения функции в дизъюнктивной нормальной форме ДНФ: F mk ,

k 1

где

L – количество групп (в том числе одиночные клетки таблицы), mk – минимизированный минтерм с количеством сомножителей равным a = n-g, n – число аргументов функции, g – степень группирования. В минтермах остаются переменные с постоянными значениями в пределах каждой группы;

для клеток с «0» необходимо найти на карте Карно минимальное количество групп нулевых ячеек и записать алгебраическое выражение по

L

следующему правилу: F mk .

k 1

Если необходимо записать алгебраическое выражение в КНФ, следует применить правило де Моргана.

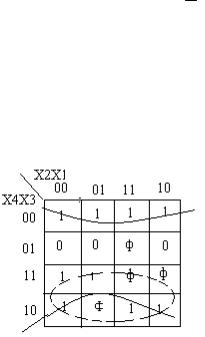
ПРИМЕР 1. Синтезировать логическое устройство для реализации функции F, заданной картой Карно (рис. 5.7). Изобразить схему устройства, используя только одну микросхему из серии К133 (155): ЛА1, ЛА4, ЛА3, ЛЕ1, ЛР1, ЛР3.

Рис. 5.7. Карта Карно для функции от четырех аргументов

Произведем группирование клеток карты по «1». При этом запрещенные значения (ф) недоопределенной функции, включенные в группу, считаются равными «1». Остальные запрещенные значения доопределяются значением «0».В результате группирования соседних единичных клеток в две группы получим

67

алгебраическое выражение логической функции в ДНФ, содержащей два минтерма. Оба минтерма содержат по одной переменной. Это следует из того, что обе группы содержат по 8 клеток и степень их группирования составляет g = 3. В минтермах остаются переменные с постоянным значением в пределах группы. Таким образом, получаем следующее минимизированное алгебраическое выражение для заданной функции: F X4 X3.

.Реализуем схему логического устройства в базисе 2ИЛИ-НЕ на микросхеме 155ЛЕ1. Для этого преобразуем алгебраическое выражение в базис 2ИЛИ-НЕ.

F X4 X3 Функциональная схема устройства, отражающая последнее алгебраическое выражение приведена на рис. 5.8.

Реализуем схему логического устройства в базисе 2И-НЕ на микросхеме 155ЛА3. Используя правила де Моргана, преобразуем минимизированное выражение в базис 2И-НЕ F X4 X3 X4 X3. Функциональная схема разработанного устройства приведена на рис. 5.9.

155ЛЕ1

(7402)

2

3 1 1

5

6 1 4

8

9 1 10

11

12 1 13

Рис. 5.8. Функциональные схемы микросхемы 155ЛЕ1 и цифрового устройства на ее базе для примера 1

Рис. 5.9. Функциональные схемы микросхемы 155ЛА3 и цифрового устройства на ее базе для примера 1

ПРИМЕР 2. Синтезировать логическое устройство для реализации функции, заданной таблицей истинности (табл. 5.4). Изобразить схему устройства, используя только одну микросхему из серии К133 (155): ЛА1, ЛА4, ЛА3, ЛЕ1, ЛР1, ЛР3.

Заполняем карту Карно и объединим соседние единичные клетки (рис. 5.11). В результате группирования соседних единичных клеток получим

68

алгебраическое выражение логической функции в ДНФ, содержащей один минтерм с двумя переменными F X4 X3.

Реализуем схему логического устройства в базисе 2И-НЕ на микросхеме

155ЛА3. Преобразуем алгебраическое выражение в указанный базис F X4 X3. Функциональная схема устройства, эквивалентная этому алгебраическому выражению, приведена на рис. 5.12.

Рис. 5.11. Карта Карно для примера 2

Рис. 5.12. Функциональная схема цифрового устройства для примера 2

69