Динамика полета. Расчет траекторий самолетов учебное пособие. Пентюхов В.И., Будник А.П

МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

В.И. ПЕНТЮХОВ А.П. БУДНИК

ДИНАМИКА ПОЛЕТА

Расчет траекторий самолетов учебное пособие

Воронеж 1999

3

УДК 629.7.015.001.24

Динамика полета; расчет траекторий самолетов: Учеб. пособие/ В.И.Пентюхов, А.П.Будник; Воронеж. гос. техн. ун-т. Воронеж 1999. 107с.

В учебном пособии изложены вопросы, связанные с расчетом траекторий современных самолетов. Приведены

технических работников, желающих ознакомиться с с о- временными методами расчета траекторий самолета.

Рукопись набрана в текстовом редакторе Word 7.0 и размещена на дискете 1.44 Мбайт в виде файла Титул .doc и самораскрывающегося файла ss.exe , включающего текст учебного пособия.

Ил. 32. Библиогр.:14 назв.

Научный редактор канд. техн. наук Е.Н.Некравцев Рецензенты: кафедра 106 МАИ; канд. техн. наук В.А.Шалиткин

Печатается по решению редакционно -издательского совета Воронежского государственного технического университета

В.И. Пентюхов, А.П. Будник, 1999 Воронежский государственный технический университет, 1999

4

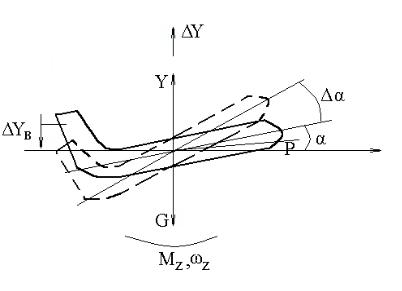
ра скорости можно осуществить, приложив момент отн о- сительно центра тяжести самолета. Для соз -

Рис 1.1 дания этого момента служит руль в ысоты .

Итак, направление полета самолета в вертикальной плоскости изменяется в следующей последовательности. После отклонения руля высоты на нем возникнет д ополнительная аэродинамическая сила , создающая м омент относительно поперечной оси, проходящей через центр т я- жести самолета. Этот момент приведет к в озникновению через некоторое время угловой скорости вращения сам о- лета относительно центра тяжести. Еще через некоторое время самолет под действием угловой скорости пове р- нется на некоторый угол относительно вектора скорости, при котором восстановится равнов есие моментов. В результате такого поворота изменится величина равноде й- ствующей аэродинамических сил. При этом равновесие сил, действующих на самолет, нар ушится, и в результате возникшего нормального ускор ения направление вектора скорости начнет изменяться, т.е. траектория п олета само-

сии с экспериментом показывает, что время со здания дополнительной результирующей силы, необход имой для

6

изменения направления движения самолета, п олучается существенно меньшим, чем время изменения направления полета. Так как при решении первой группы задач нас будет интересовать конечный р езультат рассмотренных действий, то, в первом приближении, можно пренебречь временем, необходимым для создания дополнительной р е- зультирующей силы, по сравнению с временем, необх о- димым для изменения направления полета. Другими сл о- вами, можно принять, что дополнительная внешняя сила, потребная для изменения направления полета, появляется мгновенно вслед за отклонением руля. Для большинства самолетов сила, возникающая на руле при его отклон е- нии и создающая момент относительно центра тяжести самолета, получается по величине существенно меньшей, чем остальные внешние силы. Поэтому в первом прибл и- жении можно также принять, что величина внешних сил, действующих на самолет, не зависит от положения рулей и характера движения и полностью определяется в ка ж- дый момент времени угловым положением самолета и направлением силы тяги.

Это положение, существенно упрощающее решение первой группы задач, называется гипотезой стациона рности.

Таким образом, в соответствии с гипотезой ст ационарности при определении внешних сил, действу ющих на самолет, неустановившееся движение не прин имается во внимание, и силы определяются так, как будто движение

траектории самолета, исследуя только уравнен ия равновесия сил в проекциях на оси той или иной си стемы координат, т.е. действительно позволяют при о пределении траекторий рассматривать самолет как мат ериальную точку переменной массы.

Первую группу задач можно разбить на две по д- группы.

7

К первой подгруппе относятся задачи, связанные с исследованием установившихся движений самолета, т.е. движений самолета с постоянной скоростью по прям олинейным траекториям.

Эту подгруппу задач часто называют аэродинам ическим расчетом самолета. Основы аэродинамического ра с- чета самолета разработаны Н.Е. Жуковским.

Ко второй подгруппе относятся задачи, связанные с исследованием неустановившихся и криволинейных тр а- екторий самолета.

В задачах второй группы , наоборот, подробно исследуется процесс управления самолетом и выясняется у с- тойчивость его движения по той или иной траект ории под действием различных возмущений.

В результате решения задач второй группы должна

управления самолетом , необходимый для полета по в ы- бранной траектории, и дана оценка выполнимости на й- денного закона управления. При решении задач этой группы самолет необходимо рассматривать как тело п е- ременной массы.

Эту группу задач часто выделяют под отдельным названием - устойчивость и управляемость самолета.

1.2. Внешние силы, действующие на самолет

На самолет в полете действуют массовые силы, а э- родинамические силы и сила тяги двигателей.

Полеты самолетов происходят в непосредственной близости от поверхности Земли. Поэтому из всех ма ссовых сил на движение самолета влияет только сила пр и- тяжения Земли. Остальные массовые силы незнач ительны по величине и не принимаются во внимание при иссл е- довании движения самолетов.

8

дем считать, что Земля имеет форму шара и це нтром ее притяжения является геометрический центр этого шара.

Н- высота полета.

шинстве случаев при исследовании динамики дв ижения самолетов можно принимать, что g0 = g. В этом случае связь между массой самолета и его весом о пределяется линейной зависимостью

G = g 0 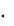m = ( 9,81 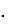m ) кГ

или в системе СИ

GС И = 9.81 G H ( ньютонов )

Кроме силы веса на самолет в полете действует це нтробежная сила, обусловленная кривизной земной п оверхности. Центростремительное ускорение, обусловле нное кривизной земной поверхности, зависит от скор ости полета и возрастает при ее увеличении. При пол ете самолета со

Поэтому в большинстве случаев динамики полета уск о- рением, обусловленным кривизной земной повер хности,

9

основании продувок моделей в трубах или путем те оре-

10

нейшем пользоваться вышеприведенными формулами. Сила тяги, необходимая для полета самолета, созд а-

ется установленным на нем движителем.

С точки зрения механики в основу всех движит елей положен один принцип: отбрасывание рабочего т ела в сторону, противоположную желаемому движению.

Источником энергии для движителя является дв игатель. По составу рабочего тела двигатели можно разд е- лить на ракетные, воздушно - реактивные и винтовые. На современных самолетах применяют в основном возду шно

-реактивные и турбовинтовые двигатели.

Увоздушно - реактивных двигателей рабочее тело состоит из воздуха и продуктов сгорания горючего, н а- ходящегося на борту самолета. У винтовых двигат елей

расхода топлива, т.е. часового расхода топлива, пр иходящегося на 1 кГ тяги (на 1 л.с. мощности), от ск орости, высоты полѐта и числа оборотов двигателя н азываются характеристиками двигателя. Обычно характ еристики двигателей подразделяют на скоростные, в ысотные и дроссельные.

1.3. Системы координат

11

В динамике полета самолета наиболее широко пр и- меняются следующие системы координат.

и направлена так, чтобы система координат была пр авой. Связанная с самолетом система координат . Начало связанной системы координат помещается в центре масс

самолета. Оси x1 , y1 , называемые продольными и поп е- речными осями самолета , расположены в вертикальной плоскости самолета и направлены вдоль гла вных осей

инерции вперед по полету и верх соответс твенно. Ось z1

перпендикулярна плоскости x1y1 и направлена так, чтобы система координат была правой. Пол ожение связанной системы координат относительно зе мной определяется

горизонтальной плоскостью x1 и направлением оси свя-

системы координат помещается в центре масс с амолета. Ось x направлена по вектору скорости полета относ и-

12