
2085
.pdf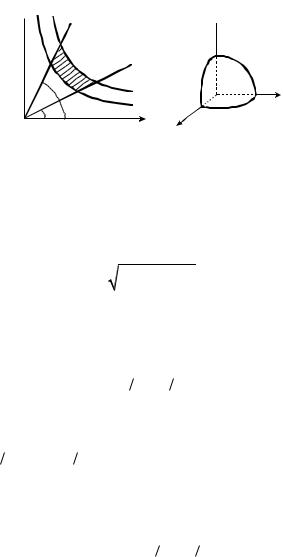
y


|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
= |
|
|
|
|
= |
2 |
x |
G |
x |
|
|
|
|
|
|
|
|
||||
y |
2 |
xy= |
|
|||||
|
|
|
||||||
|
|
|
|
|||||
|
|
|
|
|
xy |
|
2 |
|
|
|
|
|
|
= |
|
|
|
|
|
|
1 |
|
1 |
|
|
x |
|
|
|
|
|
|
x |
||
|
|
|
|
|
|
|
||
z
R
0 |
R y |
R
Рис. 21 |
Рис. 22 |
Пример 6. Найти координаты |
центра масс части шара |
x2 y2 z2 R2, расположенной в первом октанте, если плотность в каждой точке обратно пропорциональна расстоянию точки от начала координат.
Решение. Имеем x,y,z |
|
k |
k - коэффици- |
||
|
|
|
, где |
||
|
|
|
|||
|
|||||
|
|
x2 y2 z2 |
|
||
ент пропорциональности, и, вследствие симметрии, xc yc zc .
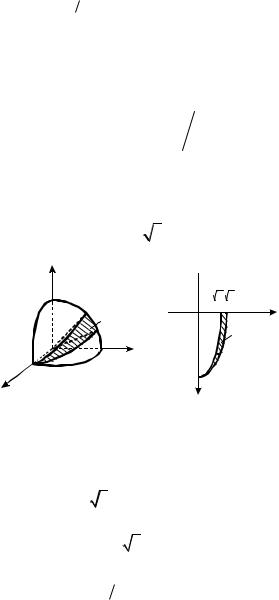
Вычислим статический момент тела (рис. 22) относительно плоскости yOz . Вычисления будем проводить в сферической системе координат, тогда получаем
Myz x x, y,z dv |
2 |
|
|
2 |
|
|
R |
|
|
|
|
|
|
k |
r2dr |
|||
|
d |
sin d rcos sin |
||||||||||||||||
|
|
|||||||||||||||||
T |
|
0 |
|
|
0 |
|
0 |
|
|
|
|
|
|
r |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
2 |
|
R |
|
|
|
|
|
R3 |
|
|
kR3 |
|
|
||||
k |
cos d sin2 d r2dr k 1 |
|
|
. |
||||||||||||||
|
|
|
|
|||||||||||||||
0 |
0 |
|
|
0 |
|
|
4 |
3 |
|
12 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вычисляем массу тела |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
2 |
|
|
|
R |
|
|
|
|
|
|
|||
m x, y,z dxdydz |
|
d |
sin d |
k |
r2dr |
|||||||||||||
|
||||||||||||||||||
T |
|
|
0 |
|
0 |
|
|
0 |
|
r |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
111
|
|
|
|
2 k |
r2 |
|
R |
|
|
1 1 k |
R2 |
|
|
|
kR2 |
. |
||||||||||||||
|
cos |
|
|
|||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2 |
|
|
0 |
2 |
|
0 |
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В итоге получаем координаты центра масс |
|
|
|
|
|
|||||||||||||||||||||||||
|
x y z |
Myz |
|
kR3 |
|
|
kR2 |
|
|
R |
. |
|
||||||||||||||||||
|
|
c c |
c |
|
|
m |
12 |
|
2 |
|
|
|
6 |
|
|
|||||||||||||||
Пример 7. Найти площадь части сферы x2 y2 z2 1, |
распо- |
|||||||||||||||||||||||||||||
ложенной между плоскостями |
z |
|
|
y |
|
и |
z y |
(x 0, |
y 0, |
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
3 |
||||||||||||||||||||||||||||||
z 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
_2 |
_3 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
y |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
||||||||
|
|
1 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|||||||||
Рис. 23
Решение. Изображаем поверхность G , площадь которой требуется найти (рис. 23,а). Чтобы найти уравнение проекции линии
пересечения плоскости z |
y |
и сферы x2 y2 z2 1 под- |
||||||||||||
|
|
|
|
|||||||||||
3 |
|
|||||||||||||
|
|
|
|
|
|
y |
|
|
|
|||||
ставляем в уравнение сферы z |
|
|
. Получаем, что проекцией |
|||||||||||
|
|
|
|
|||||||||||
3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
является |
часть эллипса |
x2 |
|
y2 |
|
1. Чтобы найти |
уравнение |
|||||||
1 |
|
|
|
|||||||||||
|
|
|
3 4 |
|
|
|
|
|
||||||
проекции |
линии пересечения |
|
плоскости z y |
и сферы |
||||||||||
|
|
|
|
112 |
|
|
|
|
|
|
||||
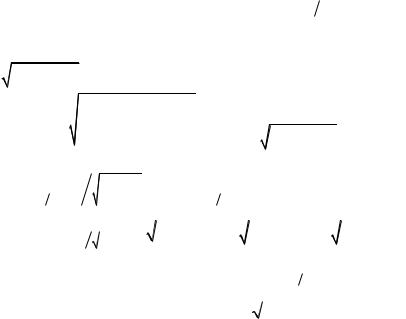
x2 y2 z2 1 подставляем в уравнение сферы |
z y. Получа- |
|||
|
x2 |
|
y2 |
|
ем, что проекцией является часть эллипса |
|
|
|
1. Изобра- |
1 |
|
|||
|
1 2 |
|
||
жаем проекцию D поверхности G на плоскость xOy
(рис. 23 ,б). Записываем уравнение верхней половины сферы
z |
1 x2 y2 |
и вычисляем искомую площадь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
Q |
|
z 2 |
z 2 |
|
|
|
|
|
|
|
|
dxdy |
|
|
|
|
|
|
|
|
|
x rcos |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y rsin |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
D |
|
|
|
x |
|
|
|
|
y |
|
|
|
|
|
|
D 1 x2 y2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
1 |
1 |
sin2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
3 |
|
|
|
|
|
rdr |
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 r |
2 |
0 |
|
|
|
4 cos |
2 |
|
|
|
|
|
|
|
|
2 cos |
2 |
|
|
|
|||||||||||||||||
|
|
1 |
1 sin2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
cos |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
arcsin |
|
|
|
|
|
|
arcsin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Задачи и упражнения для самостоятельного решения
Решить задачи№№ 8.75, 8.92, 8.93, 8.94, 8.98, 8.130, 8.137, 8.142, 8.147 [19].
Форма отчетности: устный опрос, контрольная работа.
ЗАНЯТИЕ № 30
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ТЕОРЕМА КОШИ И ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ
113

Литература: [22], с. 117-125; [27], с. 32-46; [28], с. 142-157; [34], c. 42-53.
Контрольные вопросы и задания
1.Дайте определение интеграла от функции комплексного переменного.
2.Как вычислить интеграл от функции комплексного переменного?
3.Сформулируйте теорему Коши для простого и сложного контура.
4.Как применяется интегральная формула Коши для вычисления интегралов по замкнутым контурам?
Примеры решения задач
Пример 1. Вычислить e |
|
z |
|
2 |
Rezdz, где C - отрезок прямой, |
|
|
||||
|
|
||||
C |
|
||||
соединяющей точки z1 0 и z2 1 i .
Решение. Выделим действительную и мнимую часть подынте-
гральной функции |
f z e |
|
z |
|
2 |
Rez. Для этого перепишем ее в |
||||||
|
|
|||||||||||
|
|
|||||||||||
виде e |
|
z |
|
2 |
Rez ex2 y2 x. Отсюда следует, что u x, y xex2 y2 |
, |
||||||
|
|
|||||||||||
|
|
|||||||||||
v x,0 0. Применим формулу f z dz |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
C |
|
u x, y dx v x, y dy i v x, y dx u x, y dy. Получаем, |
|
|||||||||||
C |
|
C |
|
|
||||||||
что вычисление f z dz сводится к вычислению двух криво-
C
линейных интегралов: ez 2 Rezdz xex2 y2 dx i xex2 y2 dy .
C C C
Уравнение отрезка прямой, проходящей через точки z1 0 и z2 1 i , будет y x , где 0 x 1, а значит dy dx. Поэтому
114

|
|
z |
|
2 |
1 |
|
2x2 |
1 |
2x2 |
|
|
|
1 |
|
2x2 |
|
1 |
|
1 |
|
2x2 |
|
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
e |
|
|
|
|
Rezdz xe |
dx i xe |
|
dx |
|
e |
|
|
|
i |
|
e |
|
|
|
|||||||
|
|
|
|
|
4 |
|
|
|
4 |
|
||||||||||||||||
C |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
e2 1 i |
1 |
e2 1 |
1 |
e2 1 1 i . |
|
|
|
|
|||||||||||
|
|
|
|
|
4 |
4 |
4 |
|
|
|
|
|||||||||||||||
Пример 2. Вычислить |
zkdz , |
где C - окружность единичного |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
радиуса с центром в точке z 0 (обход против часовой стрелки, k - целое число).
Решение. Так |
как на окружности |
C |
|
z |
|
1, |
то z ei ( |
|||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
0 2 ) и dz iei d . Тогда zkdz eik iei d |
||||||||||||||
|
|
|
|
|
|
C |
|
0 |
|
|
|
|
||
|
2 |
ei k 1 d i |
2 |
cos k 1 isin k 1 d |
||||||||||
i |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
sin k 1 |
|
cos k 1 |
|
2 |
|
0, |
k 1 |
|||||
|
|
|
|
|
||||||||||
i |
|
|
|
|
|
|
|
|
|
|
. |
|||
k 1 |
k 1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
0 |
|
|
|
2 i, k 1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При k 0 результат вычислений согласуется с теоремой Коши.
При k 1 |
функция f z |
1 |
не определена и не дифференци- |
|
|
||||
|
|
|
z |
|
руема |
в |
точке z 0. Интеграл не равен нулю. При |
||
k 2, |
3, подынтегральная функция не определена в точке |
|||
z 0 и теорема Коши также не применима, но интеграл равен нулю.
Пример 3. Вычислить |
zzdz, где C: |
z |
1. |
|
|
|
|
C |
|
|
|
Решение. Аналогично примеру 2 |
|
|
|
115 |
|
|
|

|
2 |
2 |
|
2 |
|
|
zzdz ei e i iei d ei d i ei |
|
|
||
|
0 |
||||
|
|
||||
C |
0 |
0 |
|
|
|
|
e2 i |
1 cos2 isin2 1 0. |
|
|
|
|
|
1 i |
|
|
|
Пример 4. Вычислить интеграл zdz .
i
Решение. Так как подынтегральная функция является аналитической, то можно использовать формулу Ньютона-Лейбница:
1 i |
|
|
|
|
|
|
z2 |
|
1 i |
|
|
1 |
1 i 2 |
i2 |
|
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
zdz |
|
|
|
|
i. |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
i |
|
|
|
|
|
|
|
2 |
|
i |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ez |
|
dz , где C- окружность: а) |
|
z |
|
|
||||||||
Пример 5. Вычислить |
|
|
|
2, |
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
z 3 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
z |
|
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение. |
|
|
C - окружность радиуса 2, то подынтегральная |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
а) |
Если |
||||||||||||||||||||||
функция |
|
|
|
ez |
|
является аналитической в каждой точке круга |
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
|
z |
|
|
|
|
|
|
|
|
|
|
z 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
(рис. |
|
|
24,а). |
Поэтому, в силу теоремы |
|
Коши |
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
ez |
dz 0. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
z |
|
|
z 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y |
y |
| |
|
|
z |
|
|
| |
|
|
= |
|
| |
4 |
|
z |
|
|
| |
|
|
= |
|
|
2 |
|
z0=-3 0 |
x z0=-3 0 |
x |
y
|z=| 3
z0=0
x
а) б) в)
116
Рис. 24
б) Если C - окружность радиуса 4, то точка z 3 (в ней
функция не определена) принадлежит кругу |
|
z |
4 (рис. |
|
24,б). |
||||||||||||||||||||||||||||||||||||||||||
Представим |
подынтегральную |
функцию |
|
в |
виде |
|
f z |
|
, |
|
|
|
где |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z z0 |
|
|
||||||
f z ez является аналитической в каждой точке круга |
|
z |
|
|
4. |
||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||
Применим |
|
|
интегральную |
формулу |
|
Коши |
|
|
(z0 3) |
||||||||||||||||||||||||||||||||||||||
f z0 |
1 |
|
|
|
f z |
|
|
|
|
|
|
|
|
|
|
|
|
ezdz |
|
|
|
|
|
|
|
|
|
2 i |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
C |
|
|
|
|
dz . Получим |
z |
|
4 |
|
|
|
|
2 iez |
|
|
|
|
. |
|||||||||||||||||||||||||||
|
2 i |
z z0 |
z 3 |
z 3 |
e3 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
cosz |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Пример 6. Вычислить |
dz, где C: |
|
z |
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
z |
|
|
|
|
|
|
cosz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. Подынтегральная функция |
|
|
является аналитиче- |
||||||||||||||||||||||||||||||||||||||||||||
z3 |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ской в круге |
|
|
3 всюду кроме точки z0 |
|
0 |
|
(рис. 2,в). Выде- |
||||||||||||||||||||||||||||||||||||||||
лим под знаком интеграла функцию f z cosz , |
являющуюся |
||||||||||||||||||||||||||||||||||||||||||||||
аналитической |
в круге |
|
|
z |
|
3. |
Воспользуемся |
интегральной |
|||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||
формулой |
|
|
|
Коши |
|
|
для |
|
|
производной |
|
|
f n |
z |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
f z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||||
|
n! |
|
|
|
dz . При z0 0 |
и n 2 получим |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
2 i |
z z |
0 |
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosz |
|
2 i |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dz |
cosz |
|
|
|
i. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
z |
|
3 |
z |
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
z 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Задачи и упражнения для самостоятельного решения
1) Вычислить интегралы:
117

|
|
|
|
|
|
i |
|
|
|
i |
i |
|
|
||||
|
|
|
|
|
|
а) zezdz ; |
|
б) zcoszdz ; |
в) 3z3 2z2 dz . |
||||||||
|
|
1 |
|
|
|
|
0 |
|
|
1 |
|
|
|||||
2) |
Вычислить интегралы: |
|
|
|
|||||||||||||
а) |
|
zImz2dz, где C : |
|
|
|
Im z |
|
1, Rez 1 ; |
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
C |
|
|
|
|
dz , где C : |
|
|
|
1, Imz 0 ; |
|
|
|
||||
б) |
z |
|
z |
|
|
z |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) |
zRez2dz , где AB - отрезок прямой, |
zA 0, |
zB 1 2i. |
||||||||||||||
|
AB |
|
|
|
|
|
|
|
|
|
|||||||
3)Вычислить с помощью интегральной формулы Коши следующие интегралы:
|
|
|
|
|
e |
iz |
|
|
|
|
|
|
|
dz |
|
|
|
|
|
|
|
sin |
z |
|
|
||||||
а) |
|
|
|
dz; б) |
|
|
; в) |
|
|
2 |
dz ; |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
||||||||||||||||
|
z i |
|
1 |
z |
|
|
1 |
|
|
|
z |
|
5 |
z |
16 |
|
z 1 |
|
2 |
z |
|
2z 3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
sh |
2 |
|
|
|
|
|
|
|
|
|
1 z |
|
|
|
|
|
|
|
|
|
|
|
|
|
г) |
z |
dz ; д) |
|
|
e |
|
dz. |
|
|
|
|
|
||||||||||||||||
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
z |
|
1 |
z |
|
|
|
|
|
|
z 2i |
|
1 |
z2 4 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Форма отчетности:устный опрос, типовой расчет, коллоквиум.
ЗАНЯТИЕ № 31-35
РАЗЛОЖЕНИЕ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО В РЯДЫ ТЕЙЛОРА И ЛОРАНА.
ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ И ИХ КЛАССИФИКАЦИЯ
Литература: [21] с. 125-132; [23], с. 46-70; [12], с. 160-172; [34], c. 55-66.
118
Контрольные вопросы и задания
1) Запишите ряд Тейлора для функции комплексного перемен-
ного f z , аналитической в круге |
z z0 |
R. Как опреде- |
ляются его коэффициенты? |
|
|
2)Сформулировать теорему Тейлора. Каковы условия разложимости функции в ряд Тейлора?
3)Записать разложения в ряд Тейлора для основных элементарных функций: ez , sinz, cosz , Ln 1 z , 1 z a , arctgz
4) Дать определение ряда Лорана функции f z . Как опреде-
ляются его коэффициенты?
5)Сформулировать теорему Лорана. Каковы условия сходимости ряда Лорана? Какова его область сходимости?
6)Какие ряды называются правильной и главной частями ряда Лорана?
7)Какая точка называется особой точкой функции? В каком случае она называется изолированной особой точкой?
8)Какая особая точка называется:
|
а) устранимой; б) полюсом; в) существенно особой? |
|||
9) |
Как зависит вид ряда Лорана от характера особой точки? |
|||
10) |
Как связаны полюсы функции |
1 |
с нулями функции |
|
f z |
||||
|
|
|
||
f z ? Что такое кратность полюса?
Примеры решения задач
Пример 1. Разложить f z |
1 |
в окрестности |
1 z2 z2 4 |
||
точки z 0 в ряд Тейлора. |
|
|
119

Решение. Представим f z в виде суммы двух дробей:
f z |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
1 |
1 |
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и воспользуемся |
||||||||||||||||||||||||||||
5 |
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 z2 |
|
|
|
|
4 |
|
|
5 1 z2 |
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
разложением в ряд |
|
|
zn , |
сходящемся в круге |
|
z |
|
1, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 z |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
подставляя |
вместо |
z для |
первой |
дроби z2, а |
для |
второй - |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
|||||||||||||||||
|
z |
|
. |
Получим ряд Тейлора f z |
1 |
|
z2n |
|
z2n |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 5 |
|
4 |
n 1 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
1 |
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1 |
|
|
|
|
|
z2n , который сходится в круге |
|
z |
|
1. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
5 n 0 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f z |
|||||||||||||
Пример |
|
|
2. |
|
|
Разложить |
|
в |
|
|
ряд |
Лорана |
|
функцию |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
в областях: |
а) |
|
z |
|
|
1; б) |
1 |
|
z |
|
2; в) |
|
z |
|
2. |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
1 z z 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Решение. |
|
Представим |
|
|
в |
виде |
|
суммы |
двух |
|
дробей: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
f z |
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
1, то |
|
zn , |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Если |
|
|
|
|
|
|
|
|
|
|
|
а если |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
1 z |
|
|
|
|
|
z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 z |
n 0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
z |
|
1, то |
1 |
|
|
||||
|
|
|||
|
|
|
1 z |
|
|
|
|
||
имеем разложение
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
. Аналогично, при |
|
z |
|
2 |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
1 |
|
|
|
n |
|||||||||||||||||
|
n 1 z |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
z 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
z |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 n zn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 , а если |
z |
2, |
||||||||
z 2 |
|
|
|
|
|
|
|
z |
|
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
1 |
|
|
|
|
|
n 0 |
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
120
