Метод Неймана-Пирсона

Если стоимости потерь от ошибочно принятых решений неизвестны, правило постановки диагноза можно установить из условия минимума значения вероятности одной из ошибок диагностирования при заданном (допустимом) уровне другой. По методу Неймана - Пирсона минимизируется вероятность ошибки 2-го рода (пропуска дефекта) Р_м, см. второе соотношение в (26), при условии, что вероятность ошибки 1-го рода (ложной тревоги) P_F не превышает заданного значения :

(31)

Этот уровень устанавливается на основе опыта эксплуатации объектов или интуитивных соображений с учетом разрешающей способности диагностических средств, степени опасности дефектов и экономических затрат. В практических расчетах принимают

(32)

где k – коэффициент избыточности, выбираемый из диапазона 1...3, если пропуск дефекта приводит к несущественным потерям, или из интервала 3...10, если пропуск дефекта влечет катастрофические последствия.

Соотношение (31) определяет пороговое значение . Уравнение граничной поверхности в пространстве параметров и правило постановки диагноза по-прежнему описываются формулами (24) и (25).

Можно использовать другой подход – определить пороговое значение исходя из допустимой вероятности пропуска дефекта (ошибки 2-го рода) Р_м:

.

Если пропуск дефекта влечет тяжелые последствия нежелателен, принимают

,

где N –общее число контролируемых объектов, k = 1,..., 10 – коэффициент избыточности.

Еще раз отметим, что для упрощения вычислений во всех вышеприведенных формулах вместо отношения правдоподобия можно использовать монотонную функцию – логарифм этого отношения.

Пример. Рассмотрим диагностику по двум параметрам х = (x₁,x₂), имеющим нормальное распределение в состояниях D₀ и D₁. Параметры будем считать статистически независимыми, то есть их совместная плотность вероятности равна произведению плотностей вероятности распределения каждого параметра:

;

где ,(i = 0,1) – средние значения параметров, a и– среднеквадратические отклонения параметров в состояниях D₀ и D₁. Логарифмируя обе части (25), находим правило постановки диагноза по методу минимального риска

.

Если в этой формуле знаки неравенства заменить на знак равенства, получим уравнение граничной линии второго порядка на плоскости диагностических параметров (x₁,x₂). В случае равенства среднеквадратических отклонений (j=1,2) правило упрощается:

.

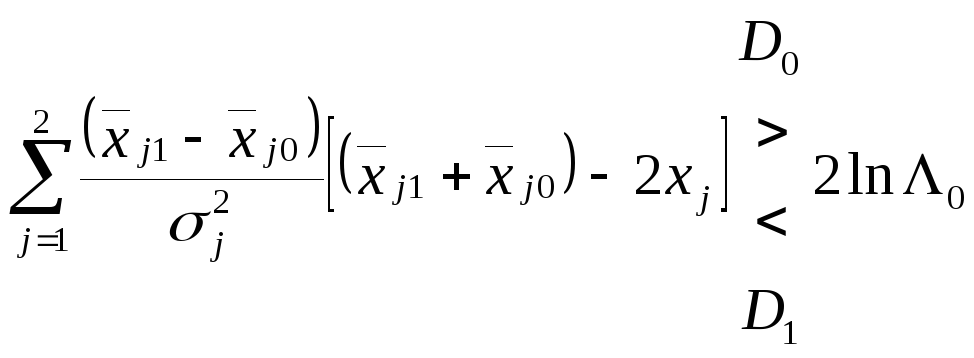Задача 2. Состояние подшипника циркуляционного насоса контролируется по содержанию металла в смазке, появляющегося в результате износа конструкционных элементов подшипника. Предварительно установлено, что концентрация металла подчиняется нормальному закону распределения, причем в исправном состоянии D₀, среднее содержание металла составляет х₀=0,5 мг/кг при среднеквадратическом отклонении =0,2 мг/кг, а для предельно изношенногосостояния D₁ эти величины соответственно равны х₁=1,5 мг/кг, =0,3 мг/кг. Используя различные статистические методы принятия решений, определить предельное содержание металла в смазке, при котором подшипник подлежит разборке и ремонту, если их стоимость в условных величинах составляет П₀₁ =10 единиц, а последствия аварийной ситуации, связанной с остановкой, оцениваются в П₁₀ = 200 единиц. Априорные вероятности исправного и изношенного состояний подшипника на момент диагностики соответственно равны Р(D₀)=0,95 и P(D₁)=0,05.

Метод минимального риска

Плотности вероятностей распределения диагностического параметра – концентрации металла в смазке – при нормальном и изношенном состоянии подшипника описываются функциями

Составив отношение правдоподобия и прологарифмировав обе части соотношения (24), получим уравнение для определения критической концентрации (граничное значение) металла в смазке:

(34)

Здесь, поскольку выигрыш от правильно поставленных диагнозов, они приняты равными нулю. Введя обозначение z=уравнение (34) можно записать в виде

(35)

где

Подставив исходные данные, определяем положительный корень уравнения (35) – z=1,842. Следовательно, мг/кг. Вероятности ошибок 1-го и 2-го рода, см. рис. 1 вычисляются по формулам (20), которые в нашем случае имеют вид:

(36)

В результате вычислений находим . Средний риск равен усл. ед.

Метод минимального числа ошибочных решений

Критическую концентрацию металла в смазке определяем из уравнения (34), положив в правой его части .

В результате вычислений находим мг/гк. Вероятности ошибок 1-го и 2-го рода вычисляются по формулам (36) при найденном значении:и. Средний риск составляетусл. ед.

Метод максимального правдоподобия

Критическую концентрацию металла в смазке вычислим из уравнения (34), положив в правой его части П₀₁P(D₁)= П₀₁P(D₀), (см. п. 2.3). При этом уравнение (34) для определения х^* принимает вид:

Решив это уравнение, находим х^* =0,92 мг/кг. Вероятности ошибок 1-го и 2-го рода рассчитываются согласно (36) при найденном значении х^*: Р_F = 0,0161 и Р_м = 0,00137. Средний риск составляет величину R = 0,44 усл. ед.