
- •Оглавление
- •Общие положения о безопасности жизнедеятельности
- •Обеспечение безопасности основных технологических процессов и оборудования машиностроительного предприятия Литейное производство
- •Кузнечно-прессовое производство
- •Термическая обработка деталей
- •Механическая обработка материалов резанием
- •Механизированные способы удаления стружки
- •Сварочные работы
- •Введение в техническую диагностику потенциально опасных объектов машиностроительного предприятия
- •Термины и определения
- •Пределы
- •Методическое обеспечение технического диагностирования объектов машиностроения
- •Цели и задачи диагностики
- •Оценка приоритетов
- •База для принятия решений
- •Свойства металла сварного соединения трубопроводов Ду 500
- •Результаты испытаний на малоцикловую усталость
- •Применение статистических методов распознования принятия решений при диагностике оборудования машиностроительного предприятия
- •Понятие диагностических параметров и признаков
- •Метод Байеса
- •Метод минимального риска
- •Метод максимального правдоподобия
- •Метод минимакса
- •Метод Неймана-Пирсона
- •Метод минимакса
- •Метод Неймана – Пирсона
- •Данные расчетов с помощью методов статистических решений
- •Метод минимального риска
- •Технические средства и методы защиты атмосферы
- •Основные свойства пыли и их определение Дисперсность пыли
- •Плотность частиц пыли
- •Удельная поверхность
- •Сыпучесть пыли
- •Гигроскопичность пыли
- •Смачиваемость пыли
- •Абразивность пыли
- •Электрические свойства пыли
- •Технические средства и методы защиты атмосферы Классификация пылеулавливающего оборудования
- •Циклоны типа сиот
- •Циклон с обратным конусом цок
- •Золоуловители батарейные типа бц - 512
- •Золоуловители батарейные типа бц - 259
- •Циклон типа оэкдм
- •Циклон водяной пленкой типа цвп
- •Список литературы
- •Техническая диагностика./Биргер и.А. – м.: Машиностроение, 1978. – 240с.
Метод Байеса
Метод Байеса принятия решений о состоянии диагностируемых объектов основан на использовании обобщенной формулы Байеса. Для ее применения требуется большой объем предварительной информации, которая может быть накоплена в процессе эксплуатации объектов или в результате специально организованных экспериментальных исследований. При наличии необходимых данных с помощью метода Байеса можно оценить состояние объектов с высоким уровнем распознавания (см. ниже), поэтому его относят к эффективным методам принятия решений.
Будем считать, что диагностируемый объект может находиться в одном из возможных состояний Di (i=0, 1,...,N) и характеризуется сложным признаком k=(k1, k2,..., km). В соответствии с методом Байеса рассчитываются условные вероятности P(Di / k) = P(Di / kl, k2,...,km). Это –апостериорные, то есть установленные после диагностирования, вероятности состояний Di при условии, что объект обладает признаком k. Решающее правило – правило принятия решения о нахождении объекта в состоянии Di – состоит в том, что объект с комплексным признаком k относят к указанному состоянию, если апостериорная вероятность этого состояния максимальна
P(Di/k) >P(Dj/k), j = 0,1,..., N; i ¹j (1)
Это правило усиливают введением уровня распознавания Р* , обычно Р*³0,9. Решение о диагнозе Di принимается, если выполнены условия (1) и P(Di/k)³ Р*.
При этом вероятность альтернативных диагнозов не превышает 1–Р*. В ином случае отказываются от постановки диагноза, для постановки которого требуется дополнительная информация.
Рассмотрим процедуру определения апостериорных вероятностей P(Di/k). Вероятность двух событий – нахождения объекта в состоянии Di и наличия у него сложного признака k – определяется формулами теории вероятностей
P(Di, k) = P(Di) P(k/Di)=P(k) P(Di/k) (3)
где P(Di) – априорная (известная до диагностирования по результатам специально проведенных предварительных исследований) вероятность состояния Di; P(k/Di) – условная вероятность наличия у объекта признака k, если он находится в состоянии Di, P(k) – вероятность наличия у объекта комплексного признака k независимо от его состояния. Поскольку объект при любом k может находиться только в одном состоянии, то
![]() (4)
(4)
Просуммировав обе части правого равенства в (3) по i, определим вероятность наличия у объекта признака k:
![]() (5)
(5)
С учетом этого равенства из (3) следует обобщенная формула Байеса для вычисления апостериорных вероятностей диагнозов Di:
 (6)
(6)
Вероятности, входившие в обобщенную формулу Байеса, определяются из очевидных соображений:
![]()
![]()
![]()
![]() (7)
(7)
Здесь
![]() -
общее число продиагностированных
объектов, из которых
-
общее число продиагностированных
объектов, из которых
![]() -
число объектов с диагнозом
-
число объектов с диагнозом
![]() ;
;![]() -
количество объектов с диагнозом
-
количество объектов с диагнозом
![]() ,
имеющих комплексный признак
,
имеющих комплексный признак![]() ;
;![]() -
число объектов во всех состояниях с
признаком
-
число объектов во всех состояниях с
признаком
![]() .
.
Если компоненты комплексного признака статически независимы, то согласно формулам теории вероятности
![]() (8)
(8)
В ином случае
![]()
Обобщенная формула Байеса в случае независимости компонентов комплексного признака записывается в виде
![]()
 (9)
(9)
Задача 1.
Для диагностики подшипника в машиностроении
используются два диагностических
признака:
![]() – повышение температуры подшипника на
15°С
и более;
– повышение температуры подшипника на
15°С
и более;
![]() –
повышение уровня вибраций на 6 дБ и
более. Появление этих признаков может
быть связано с неисправностями в системе
смазки подшипника – состояние
–
повышение уровня вибраций на 6 дБ и
более. Появление этих признаков может
быть связано с неисправностями в системе
смазки подшипника – состояние![]() ,
либо с износом деталей подшипника –
состояние
,
либо с износом деталей подшипника –
состояние![]() .
Известно, что при нормальном состоянии
подшипника (состояние
.
Известно, что при нормальном состоянии
подшипника (состояние![]() )
признак
)
признак![]() не наблюдается, а признак
не наблюдается, а признак![]() наблюдается в 1%
случаев. На этапе предварительных
исследований также установлено, что
90%
подшипников вырабатывают ресурс в
нормальном состоянии, 2%
подшипников – в состоянии
наблюдается в 1%
случаев. На этапе предварительных
исследований также установлено, что
90%
подшипников вырабатывают ресурс в
нормальном состоянии, 2%
подшипников – в состоянии
![]() ,
а 8%
– в состоянии
,
а 8%
– в состоянии
![]() .
Кроме того, известно, что признак
.
Кроме того, известно, что признак![]() встречается в состоянии
встречается в состоянии![]() в 60%
случаях, а в состоянии
в 60%
случаях, а в состоянии
![]() в 20%.
Признак
в 20%.
Признак
![]() в состоянии
в состоянии![]() встречается в 30%,
а в состоянии
встречается в 30%,
а в состоянии
![]() – в 80%
случаях. Необходимо установить вероятности
состояний подшипника при различных
сочетаниях наблюдаемых признаков и их
отсутствии, полагая признаки независимыми,
то есть один из них может наблюдаться
независимо от другого.
– в 80%
случаях. Необходимо установить вероятности
состояний подшипника при различных
сочетаниях наблюдаемых признаков и их
отсутствии, полагая признаки независимыми,
то есть один из них может наблюдаться
независимо от другого.
Исходные данные
сведем в табл. 1. Так как признак
![]() (j=1,2)
либо наблюдается, либо не наблюдается
– событие
(j=1,2)
либо наблюдается, либо не наблюдается
– событие
![]() ,
при диагностике подшипника может быть
установлен один из четырех комплексных
признаков, компонентами которых являются
,
при диагностике подшипника может быть
установлен один из четырех комплексных
признаков, компонентами которых являются![]() и
и![]() ,
(j=1,2):
,
(j=1,2):
![]() =(
=(![]() );
);![]() =(
=(![]() );
);![]() =(
=(![]() );
);![]() =(
=(![]() ).
).
Таблица 1
Вероятности признаков и априорные вероятности появлений
состояний подшипника
|
|
|
|
|
|
|
0,0 |
0,01 |
0,90 |
|
|
0,60 |
0,30 |
0,02 |
|
|
0,20 |
0,80 |
0,08 |
Поскольку наблюдение
признака
![]() и его отсутствие
и его отсутствие![]() – взаимоисключающие события, условная
вероятность отсутствия признака
определяется равенством
– взаимоисключающие события, условная
вероятность отсутствия признака
определяется равенством
![]() .(10)
.(10)
Применяя обобщенную формулу Байеса (6) с учетом соотношений (8) и (10), определяем апостериорные вероятности диагнозов при наличии указанных сочетаний признаков. Например,

и т.д. Результаты расчетов сведены в табл.2.
Таблица 2
Апостериорные вероятности состояний подшипника
|
|
|
|
|
|
|
|
0,00 |
0,14 |
0,00 |
0,98 |
|
|
0,22 |
0,04 |
0,72 |
0,01 |
|
|
0,78 |
0,82 |
0,78 |
0,01 |
Из данных, приведенных
в табл.2, следует, что даже в отсутствии
признаков
![]() и
и![]() ,
то есть при наличии комплексного признака
,
то есть при наличии комплексного признака![]() =(
=(![]() ),
вероятности состояний
),
вероятности состояний![]() и
и
![]() –
–
![]() и
и![]() ,
отличны от нуля. Это означает, что
неисправности в системе смазки и износ
деталей подшипника могут и не вызвать
повышение температуры и уровня вибраций
подшипника. Эти признаки не являются
достаточными для постановки диагнозов
,
отличны от нуля. Это означает, что
неисправности в системе смазки и износ
деталей подшипника могут и не вызвать
повышение температуры и уровня вибраций
подшипника. Эти признаки не являются
достаточными для постановки диагнозов![]() и
и![]() .
Хотя вероятности таких событий очень
малы.
.
Хотя вероятности таких событий очень
малы.
При наличии обоих
признаков достоверно можно утверждать,
что подшипник неисправен. Наиболее
вероятным состоянием является износ
деталей подшипника – состояние
![]() .
В отсутствие признаков наиболее вероятно
исправное состояние (вероятность его
равна 0,98). При наличии признака
.
В отсутствие признаков наиболее вероятно
исправное состояние (вероятность его
равна 0,98). При наличии признака![]() и отсутствии
и отсутствии![]() вероятность износа – состояния
вероятность износа – состояния![]() больше. При наличии признака
больше. При наличии признака![]() и отсутствии
и отсутствии![]() больше вероятность неисправности в
системе смазки – состояние
больше вероятность неисправности в
системе смазки – состояние![]() .
Если задать уровень распознания
.
Если задать уровень распознания![]() ,
то следует констатировать, что для
достоверного определения типа
неисправности подшипника недостаточно
данных, и необходимы дополнительные
исследования.
,
то следует констатировать, что для
достоверного определения типа
неисправности подшипника недостаточно
данных, и необходимы дополнительные
исследования.
Метод последовательного анализа
Метод последовательного
анализа, или метод Вальда, используется
в основном при дихотомии, то есть тогда,
когда по результатам диагностики
необходимо принять решение о нахождении
объекта в одном из двух возможных
состояний:
![]() – исправное состояние и
– исправное состояние и![]() – неисправное состояние.
– неисправное состояние.
Для пояснения
сущности данного метода рассмотрим
отношение апостериорных вероятностей
диагнозов
![]() и
и![]() при наличии у объекта сложного признака
при наличии у объекта сложного признака![]() ,
состоящего из независимых компонент.
Прежде всего отметим, что в случае
дихотомии по методу Байеса согласно
(1) становится диагноз
,
состоящего из независимых компонент.
Прежде всего отметим, что в случае
дихотомии по методу Байеса согласно
(1) становится диагноз![]() ,
если
,
если
 (11)
(11)
В ином случае –
диагноз
![]() .
Отношение условных вероятностей
обнаружить у диагностируемого объекта
сложного признака
.
Отношение условных вероятностей
обнаружить у диагностируемого объекта
сложного признака![]() ,
находящегося в состояниях
,
находящегося в состояниях![]() и
и![]() :
:
![]()
называется отношением правдоподобия. Через него можно выразить правило (11).
При

ставиться диагноз
![]() ,
если выполняется обратное неравенство
–
,
если выполняется обратное неравенство
–![]() .
.
По методу Вальда
проводится последовательное обследование
объекта по компонентам сложного признака
k.
На первом этапе определяется отношение
правдоподобия по первому диагностическому
признаку
![]() и выбираются верхние и нижние границы
принятия решения
и выбираются верхние и нижние границы
принятия решения![]() и
и![]() .
.
Если
 (13)
(13)
делается заключение
о состоянии
![]() .
.
Если
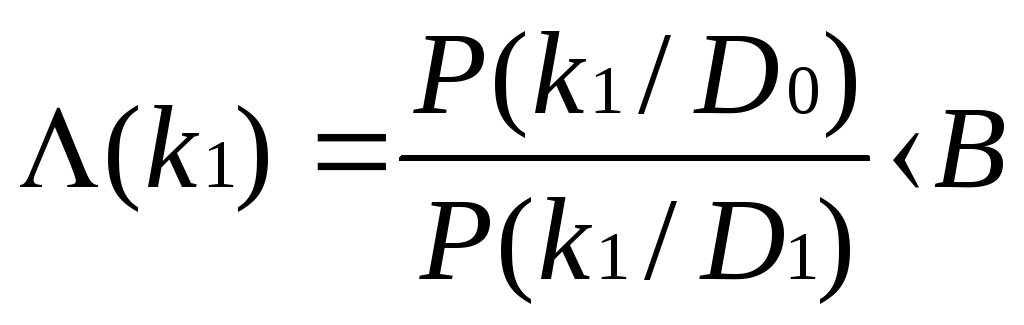 (14)
(14)
ставится диагноз
![]() .
.
Если же
 (15)
(15)
информации
недостаточно для определения состояния
объекта, и обследование проводится по
следующей компоненте
![]() .
Процедура продолжается до тех пор, пока
на каком-то этапе не будет выполнено
одно из неравенств вида (13) или (14). Если
в результате обследования все компоненты
сложного признака исчерпаны, но ни одно
из неравенств (13) и (14) не выполняется,
отказываются от постановки диагноза.
Диагностических признаков недостаточно
для определения состояния объекта.
.
Процедура продолжается до тех пор, пока
на каком-то этапе не будет выполнено
одно из неравенств вида (13) или (14). Если
в результате обследования все компоненты
сложного признака исчерпаны, но ни одно
из неравенств (13) и (14) не выполняется,
отказываются от постановки диагноза.
Диагностических признаков недостаточно
для определения состояния объекта.
Для удобства
вычислений обычно рассматривают не
отношение правдоподобия, а его монотонную
функцию – логарифм. Тогда условие
постановки диагнозов
![]() и
и![]() ,
исправного и неисправного состояния
соответственно, после
,
исправного и неисправного состояния
соответственно, после![]() – го обследования принимает соответственно
вид
– го обследования принимает соответственно
вид
 (16)
(16)
Заметим, что если обследование проводится по диагностическим параметрам, являющимся непрерывными случайными величинами, то в вышеприведенных соотношениях надо условные вероятности распределения признаков заменить на условные плотности вероятности распределения параметров.
При постановке
диагноза возможны ошибочные решения.
Если в результате диагностики принято
решение, что объект находится в неисправном
состоянии
![]() ,когда, на самом
деле, он исправен (состояние D0),
считается, что допущена ошибка 1-го рода.
Её называют еще ложной тревогой, её
вероятность обозначим через PF.
,когда, на самом
деле, он исправен (состояние D0),
считается, что допущена ошибка 1-го рода.
Её называют еще ложной тревогой, её
вероятность обозначим через PF.
Если принимается решение, что объект исправен, то есть находится в состоянии D0, когда его действительное состояние неисправное D1, допускается ошибка 2-го рода. Другое ее название – пропуск сигнала. Вероятность ошибки 2-го рода будем обозначать как Рм.
Ошибочные решения о состоянии диагностируемого объекта, как правило, приводят к потерям. Если допускается ошибка 1-го рода, и исправный объект выводится из эксплуатации, то потери могут быть связаны с затратами на ремонтные работы, в которых нет необходимости, или с недополученной выручкой от реализации продукции, производство которой приостановлено. Эти потери, выраженные в денежных единицах, обозначим через П01. В случае ошибки 2-го рода потери могут быть обусловлены затратами на ликвидацию аварии и ее последствий, если допущенный к дальнейшей эксплуатации неисправный технический объект выходит из строя, а также недополученными средствами от продажи продукции из-за остановки производства. Потери, связанные с ошибкой 2-го рода, обозначим П10. Если можно оценить выгоду при правильной постановке диагноза, то вводят выигрыши П00<0 и П11<0 – отрицательные потери. Если определить выигрыши невозможно, их полагают равными нулю. Названия, обозначения и стоимости (потери) от ошибочных решений при определении состояния диагностируемых объектов, указаны в табл.3.
Таблица 3
Ошибки и их стоимости при определении состояния технических объектов
|
Поставленный диагноз |
Истинное состояние |
Название ошибки |
Вероятность ошибки |
Обозначения потерь при принятии решений |
|
D0 |
D0 |
– |
– |
П00 |
|
D1 |
D1 |
– |
– |
П11 |
|
D1 |
D0 |
1-го рода (ложная тревога) |
РF |
П01 |
|
D0 |
D1 |
2-го рода (пропуск сигнала) |
РM |
П01 |
Если принимается решение о диагнозе D0, то вероятность правильного решения равна 1-РM. Вероятность отнесения объекта к состоянию D1 в этом случае будет равна PF. В силу (13) вероятность диагноза D0 по крайней мере в А раз превышает вероятность диагноза D1, следовательно,
![]() (17)
(17)
Аналогично можно получить следующую оценку
![]() (18)
(18)
,где РF – вероятность ошибки 1-ого рода, РM – вероятность ошибки 2-ого рода.
Соотношения (17) и (18), рассматриваемые как строгие равенства, позволяют определить верхнюю и нижнюю границы принятия решения А и В в (13)–(15) при заданных вероятностях ошибок первого и второго рода PF и РM .
ИСПОЛЬЗОВАНИЕ МЕТОДОВ СТАТИСТИЧЕСКОЙ ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ
При использовании методов статистической теории принятия решений правило постановки диагноза определяют из условия минимизации риска (см. ниже) или вероятностей ошибочных решений при диагностировании. Выбор того, какие из указанных величин минимизируются, зависит от наличия априорной информации для постановки диагноза.
Рассмотрим случай
дихотомии. Будем считать, что решение
о состоянии объекта принимается на
основе анализа диагностических параметров
в n-мерном пространстве, состояние
объекта в котором определяется вектором
диагностических параметров x
= (xl,x2,...,
хп).
Правило принятия решения о состоянии
диагностируемого объекта сводится к
определению в диагностическом пространстве
граничной
поверхности,
разделяющей его на две области S0
и S1.
Если вектор х, полученный при обследовании
объекта, принадлежит S0,
(х![]() S1),
то ставится диагноз D0.
Если x
S1),
то ставится диагноз D0.
Если x![]() S1,
принимают, что объект находится в
состоянии D1.
S1,
принимают, что объект находится в
состоянии D1.
Обозначим через w(x/Di) = w(xl,x2,...,xn/Di), (i = 0,1) условные плотности вероятности распределения вектора параметров для состояний D0 и D1. Вероятности правильно поставленных диагнозов при разбиении пространства на области S0 и S1, определяются соотношениями
 (19)
(19)
где
![]() –условные вероятности принадлежности
векторах
области Si,
когда объект находится в состоянии Di;
Р(Di)
– априорная вероятность диагноза Di;
Dx
= Dx1
Dx2...Dxn.
Вероятности ошибок 1-го и 2-го рода
вычисляются по формулам:
–условные вероятности принадлежности
векторах
области Si,
когда объект находится в состоянии Di;
Р(Di)
– априорная вероятность диагноза Di;
Dx
= Dx1
Dx2...Dxn.
Вероятности ошибок 1-го и 2-го рода
вычисляются по формулам:
 (20)
(20)
где
![]() – условные вероятности принадлежности
векторах
области Si,
когда объект находится в состоянии Dj.
– условные вероятности принадлежности
векторах
области Si,
когда объект находится в состоянии Dj.

Рис. 1. Условные плотности вероятности распределения параметра х в состояниях D0 и D1.
На рис. 1 показаны плотности вероятности распределения одного диагностического параметра х для двух различных состояний объекта. Область S0, включающая значения х<х*, отвечает диагнозу D0, область S1 (х>х*) – диагнозу D1; х*– значение диагностического параметра, разделяющего области S0 и S1. Площади различным образом заштрихованных областей пропорциональны ошибкам 1-го и 2-го рода.
