
- •Дифференциальные уравнения
- •2. Дифференциальные уравнения первого порядка.
- •Понятие об изогональных траекториях.
- •7.5. Интегрирование простейших типов д.У. 1-го порядка.
- •7.5.1. Д.У. С разделяющимися переменными.
- •7.5.3. Линейные уравнения 1-го порядка.
- •7.5.5. Д.У. В полных дифференциалах.
- •3. Д.У. 2-го порядка. Интегрирование методом понижения порядка.
- •3.1. Общие положения.
- •9. Линейные д.У..
- •9.1. Введение.
- •9.2.2. Фундаментальная система решений однородного линейного д.У.
- •9.2.3. Формула Остроградского-Лиувилля Пусть и– решения (2), следовательно,
- •9.2.4. Существование фср (2)
- •9.2.5. Применение формулы Остроградского-Лиувилля
- •9.3. Линейные неоднородные дифференциальные уравнения 2-го порядка
- •9.3.1. Теоремы о частных решениях
- •9.3.2. Метод вариации произвольных постоянных для нахождения частного решения неоднородного дифференциального линейного уравнения 2-го порядка
- •9.4. Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и приводящиеся к ним
- •9.4.1. Интегрирование однородных линейных дифференциальных уравнений 2-го порядка с постоянными коэффициентами
- •9.4.2. Неоднородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами
- •В силу следствия достаточно найти решение уравнения
- •9.4.3. Линейные дифференциальные уравнения, приводящиеся к уравнениям с постоянными коэффициентами
- •9.4.4. Линейные дифференциальные уравнения n-го порядка
- •9.5. Системы дифференциальных уравнений
- •9.5.1. …
9.3.2. Метод вариации произвольных постоянных для нахождения частного решения неоднородного дифференциального линейного уравнения 2-го порядка
Пусть
![]() , (*)
, (*)
причем
![]() – общее решение соответствующего
однородного дифференциального уравнения.
Для нахождения общего решения (*)
необходимо найти
– общее решение соответствующего
однородного дифференциального уравнения.
Для нахождения общего решения (*)
необходимо найти![]() .
Согласно методу Лагранжа,
.
Согласно методу Лагранжа,![]() ищется в виде:
ищется в виде:
![]() ,
,
где
![]() и
и![]() – неизвестны. Так как неизвестных
функций две, а уравнение одно, то
накладывается еще одно произвольное
условие с целью упростить решение. Пусть
– неизвестны. Так как неизвестных
функций две, а уравнение одно, то
накладывается еще одно произвольное
условие с целью упростить решение. Пусть
![]()
и потребуем, чтобы
![]() ,
,
– это
и есть дополнительное условие, то есть
![]() .
.
Далее,
![]() .
.
Подставим последнее выражение в уравнение (*), получим
![]() ,
,
поскольку
![]() и
и![]() .
Получили следующую систему уравнений:
.
Получили следующую систему уравнений:
 .
.
Эта
система имеет решение относительно
![]() и
и![]() ,
так как
,
так как![]() (
(![]() и
и![]() линейно независимы). Отсюда
линейно независимы). Отсюда
 ,
, ,
,
 ,
, ,
,
![]() ,
,
![]() .
.
На практике можно пользоваться сразу готовыми формулами или выводить их для конкретного уравнения.
Пример:
Рассмотрим дифференциальное уравнение
![]() .
.
Общее решение соответствующего однородного дифференциального уравнения есть
![]()
![]()
![]() и
и![]() .
.
Имеем систему уравнений

![]()

![]()
 ,
,
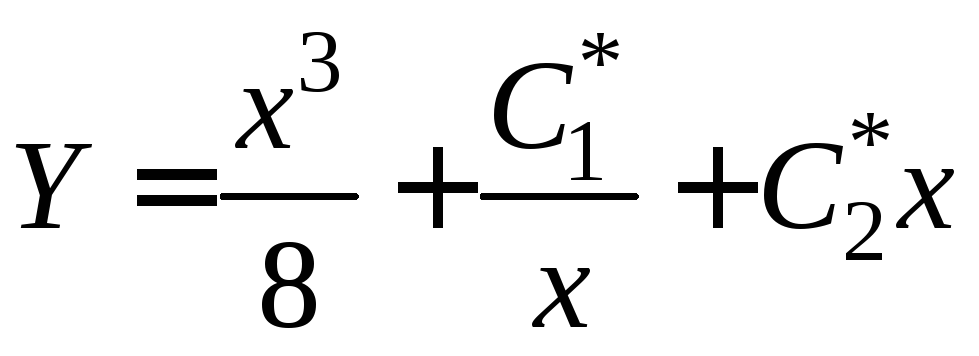 .
.
Заключение:
Таким образом, линейное дифференциальное уравнение 2-го порядка можно решить, если суметь найти частное решение неоднородного уравнения и общее решение соответствующего однородного уравнения. Стандартного процесса нахождения общего решения неоднородного уравнения нет. Многие дифференциальные уравнения не интегрируются в элементарных функциях.
9.4. Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и приводящиеся к ним
9.4.1. Интегрирование однородных линейных дифференциальных уравнений 2-го порядка с постоянными коэффициентами
Пусть дано:
![]() , (1)
, (1)
где
![]() ,
,![]() – действительные числа. Составим так
называемое характеристическое уравнение:
– действительные числа. Составим так
называемое характеристическое уравнение:
![]() (2)
(2)
и
найдем
![]() ,
,![]() – корни уравнения (2), и пусть
– корни уравнения (2), и пусть![]() .
Рассмотрим две функции:
.
Рассмотрим две функции:
![]() и
и![]() . (3)
. (3)
Докажем,
что
![]() и
и![]() есть частные решения, образующие
фундаментальную систему решений.
Подстановка дает:
есть частные решения, образующие
фундаментальную систему решений.
Подстановка дает:
![]() и
и![]() ,
,
 , (4)
, (4)
следовательно, общее решение
![]() ,
,
где
![]() ,
,![]() –
–![]() .
.
Если
![]() и
и![]() – комплексно сопряженные числа,
– комплексно сопряженные числа,![]() ,
,![]() ,
то (4) дает решение в мнимой форме. Но
можно получить и в действительной, если
перейти к
,
то (4) дает решение в мнимой форме. Но
можно получить и в действительной, если
перейти к
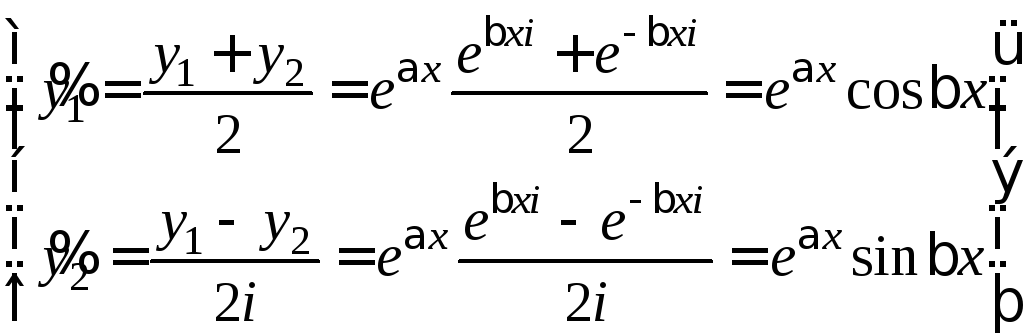
![]() (5)
(5)
![]() (6)
(6)
– общее решение.
Примеры:
1) ![]() ,
,![]() ,
,![]() .
.
2) ![]() ,
,![]() ,
,![]() .
.
3) ![]() ,
,![]() ,
,![]() .
.
Рассмотрим
теперь случай
![]() .
В этом случае
.
В этом случае![]() ,
а
,
а![]() можно получить, используя формулу
Остроградского – Лиувилля:
можно получить, используя формулу
Остроградского – Лиувилля:
![]() ,
,
 ,
,
значит,
![]() и
и![]() – фундаментальная система решений.
Общее решение будет
– фундаментальная система решений.
Общее решение будет
![]() . (7)
. (7)
9.4.2. Неоднородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами
Дано:
![]() , (8)
, (8)
![]() и
и
![]() – действительные числа, соответствующее
однородное уравнение имеет вид:
– действительные числа, соответствующее
однородное уравнение имеет вид:
![]() ,
,
характеристическое уравнение будет:
![]() .
.
При
известном общем решении однородного
дифференциального уравнения частное
решение неоднородного находится
вариацией постоянных, а затем составляется
общее решение (8). Метод вариацмм применим
к (8) при
![]() и в этом смысле универсален. Однако, для
частных случаев
и в этом смысле универсален. Однако, для
частных случаев![]() чаще применяется метод подбора.
чаще применяется метод подбора.
Общее
правило. Если
![]() может быть представлена в виде
может быть представлена в виде
![]() , (9)
, (9)
где
![]() ,
,![]() – действительные числа,
– действительные числа,![]() и
и![]() – целые рациональные функции степеней
– целые рациональные функции степеней![]() и
и![]() ,
тогда (8) имеет частное решение вида
,
тогда (8) имеет частное решение вида
![]() . (10)
. (10)
Здесь
![]() – кратность корня
– кратность корня![]() характеристического
уравнения. Если же
характеристического
уравнения. Если же ![]() не является корнем,
то
не является корнем,
то
![]() .
.![]() ,
,![]() и
и![]() – многочлены степени
– многочлены степени![]() .
Коэффициенты
.
Коэффициенты![]() и
и![]() определяются из тождества после
подстановки
определяются из тождества после
подстановки![]() в (8). Далее, как обычно, общее решение
есть сумма
в (8). Далее, как обычно, общее решение
есть сумма![]() и
и![]() .
.
Если
же
![]() не может быть сразу представлена в виде
(9), но является суммой таких выражений,
то используется теорема о наложении
решений.
не может быть сразу представлена в виде
(9), но является суммой таких выражений,
то используется теорема о наложении
решений.
Для
обоснования рассмотрим два частных
случая
![]() и выведем правила нахождения
и выведем правила нахождения![]() для каждого случая.
для каждого случая.
Случай 1.
![]() ,
,![]() ,
,![]() –
–![]() .
.
Этот
случай соответствует
![]() .
.![]() будем искать в виде
будем искать в виде![]() .
Подставим
.
Подставим![]() в (8), получим
в (8), получим
![]() ,
,
где
![]() есть:
есть:
многочлен
 -ной
степени, если
-ной
степени, если .
.многочлен
 -й
степени, если
-й
степени, если ,
, .
.многочлен
 -й
степени, если
-й
степени, если .
.
В
первом случае
![]() приходим к тождеству
приходим к тождеству
![]() , (*)
, (*)
из
которого можно найти неопределеные
коэффициенты
![]() .
.
Во
втором случае,
![]() ,
,![]() ,
то есть когда
,
то есть когда![]() есть корень характеристического
уравнения, тождество (*) невозможно, так
как степень
есть корень характеристического
уравнения, тождество (*) невозможно, так
как степень![]() на 1 меньше степени
на 1 меньше степени![]() .
Чтобы их сравнять, надо умножить
.
Чтобы их сравнять, надо умножить![]() на
на![]() .
При этом степень
.
При этом степень![]() повышается на 1. То есть мы будем искать
решение в виде
повышается на 1. То есть мы будем искать
решение в виде
![]() .
.
В
третьем случае
![]() умножается на
умножается на![]() ,
то есть
,
то есть
![]() .
.
Правило
1. Если
![]() есть
есть![]() ,
то частное решение
,
то частное решение![]() надо искать в виде
надо искать в виде
![]() ,
,
где
![]() – многочлен
– многочлен![]() -й
степени, а
-й
степени, а![]() – кратность корня
– кратность корня![]() .
Для вычисления неопределенных
коэффициентов
.
Для вычисления неопределенных
коэффициентов![]() надо подставить
надо подставить![]() в (8) и затем приравнять коэффициенты
при одинаковых степенях
в (8) и затем приравнять коэффициенты
при одинаковых степенях![]() .
.
Пример.
![]() ,
,![]() ,
корень
,
корень![]() – однократный, тогда
– однократный, тогда
![]() ,
,
![]()
![]()
![]() ,
,![]() ,
,![]() и
и
![]() .
.
Случай 2.
![]() ,
,![]() ,
,
![]() . (*)
. (*)
Сделаем
замену
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() ,
где
,
где
![]() ,
,![]() .
.
Таким образом, уравнение (*) сведено к частному случаю, рассмотренному выше. Следовательно:
Если
 ,
тогда
,
тогда

 ,
где коэффициенты
,
где коэффициенты следует определить.
следует определить.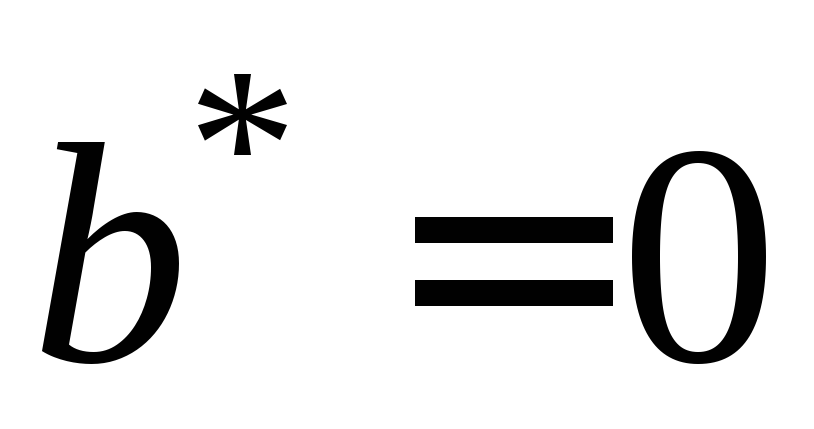 ,
,
 ,
то есть если
,
то есть если – простой корень характеристического
уравнения, то
– простой корень характеристического
уравнения, то

 .
.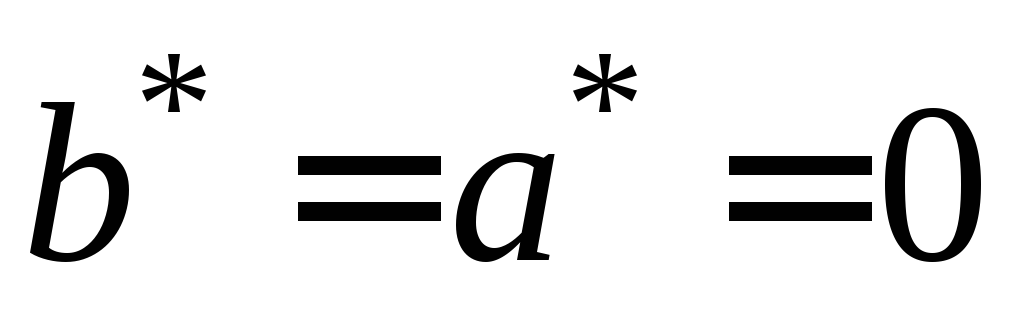 ,
то есть
,
то есть
 – двойной корень характеристического
уравнения, то
– двойной корень характеристического
уравнения, то

 .
.
Правило 2.
Если
![]() ,
то
,
то
![]() ,
,
где
![]() – кратность корня
– кратность корня![]() в характеристическом уравнении.
в характеристическом уравнении.
Пример.
![]() ,
,
![]()
![]()
![]()
![]()
![]() и
и![]() .
.
![]() ,
подставляя в дифференциальное уравнение,
получим:
,
подставляя в дифференциальное уравнение,
получим:
![]()
![]()
![]() ,
,![]() ,
,![]() .
.
![]() .
.
Перейдем теперь к общему случаю:
![]() .
.
Вспомогательная теорема.
Пусть в уравнении
![]() (*)
(*)
![]() –принимает
комплексные значения и пусть
–принимает
комплексные значения и пусть
![]() – некоторое решение. Тогда
– некоторое решение. Тогда
![]() есть
решение уравнения
есть
решение уравнения
![]() ,
,
![]() есть
решение уравнения
есть
решение уравнения
![]() .
.
Положим
![]() ,
,![]() .
Дважды дифференцируя
.
Дважды дифференцируя![]() и подставляя в (*), получим:
и подставляя в (*), получим:
![]() ,
,
отсюда, по равенству комплексных чисел, следует доказательство теоремы.
Следствие.
Если
![]() есть решение уравнения
есть решение уравнения![]() ,
то
,
то![]() есть решение уравнения
есть решение уравнения![]() .
.
Заменим
теперь в общем уравнении
![]() и
и![]() по формулам Эйлера:
по формулам Эйлера:
 ,
, ,
,
перегруппируем и введем новые обозначения:
![]() ,
,![]() ,
,![]() ,
,
тогда
![]() .
.
