1009

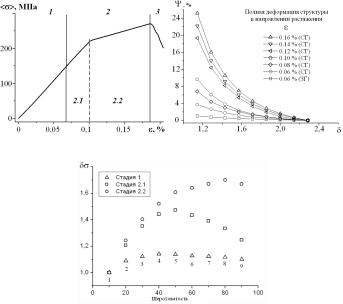
уменьшается до некоторого значения и при дальнейшем увеличении толщины покрытия изменяется незначительно (рисунок, б).

в

Рис. Кривая течения при растяжении (а), относительное изменение величины концентрации напряжений в зависимости от соотношения толщины покрытия к шероховатости границы раздела «покрытиеподложка» (б) и зависимостиотносительных концентраций напряжений от шероховатости на различных стадиях деформирования (в)

Установлено, что зависимости концентрации напряжений от шероховатости имеют нелинейный вид с характерными максимумами, причем наклон кривых зависит от стадии пластического деформирования стальной подложки (рисунок, в).

101

Список литературы

1.Balokhonov R.R., Romanova V.A. The effect of the irregular interface geometry in deformation and fracture of a steel sub- strate–boride coating composite // International Journal of Plasticity. – 2009. – 25 11. – P. 2225–2248.

2.Влияние геометрии и структуры границы раздела на характер развития пластической деформации на мезомасштабном уровне борированных образцов конструкционных сталей / С.В. Панин, А.В. Коваль, Г.В. Трусова, Ю.И. Почивалов, О.В. Сизова // Физическая мезомеханика. – 2000. – Т. 3. – № 2. – С. 99–115.

МОДЕЛЬ НЕУПРУГОГО ДЕФОРМИРОВАНИЯ ГПУ-ПОЛИКРИСТАЛЛОВ: НЕСИММЕТРИЧНЫЕ МЕРЫ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ, ЗАКОНЫ УПРОЧНЕНИЯ, РОТАЦИЯ РЕШЕТКИ

К.В. Мацюк, П.В. Трусов

(Пермский национальный исследовательский политехнический университет, Пермь)

Внастоящее время одним из интенсивно развивающихся направлений построения моделей неупругого деформирования моно- и поликристаллов являются создание и модификация физических теорий пластичности (ФТП), в основе которых лежит рассмотрение механизмов деформирования на мезо- и микроуровне. В данной работе деформирование будет рассматриваться на макро- (уровень представительного макрообъема) и мезоуровне (уровень кристаллита (зерна, субзерна)). Для описания структуры и механизмов деформирования на мезо- и микроуровне используются параметры, называемые внутренними переменными [1, 2].

Вработе предложена и реализована модификация упруговязкопластической модели ГПУ-поликристалла применительно

102

к кристаллам с гексагональной плотноупакованной решеткой (ГПУ) на примере α- титана. Такая модель позволяет учитывать влияние температуры при сложных нагружениях металла; при уменьшении скоростной чувствительности она может работать и как упругопластическая модель [3]. Использование именно упруговязкопластической модели позволяет избежать проблемы, существующей в упругопластических моделях, а именно неединственности определения скоростей сдвигов.

Рассматривается применение несимметричных мер напряженного и деформированного состояния на мезоуровне при построении конститутивных многоуровневых моделей неупругого деформирования материалов. Вводится несимметричная мера скорости деформации, не зависящая от выбора системы отсчета, описывается структура двухуровневой модели неупругого деформирования материала с использованием предложенных мер напряжений и деформаций на мезоуровне [4].

Модель учитывает такие механизмы пластического деформирования, как скольжение дислокаций и двойникование. Для описания ротации решетки использована модель стесненного поворота Тейлора. Упрочнение рассматривается отдельно для каждой из мод деформации; предложен вариант закона упрочнения для критических напряжений двойникования.

Известно, что сдвиги оказывают малое влияние на развитие двойника, в связи с чем этим влиянием можно пренебречь. В то же время двойники разных систем двойникования (СД) взаимодействуют друг с другом, ранее сформировавшиеся двойники будут повышать критические напряжения на СД, которые они пересекают. При этом двойники одной и той же СД будут образовывать двойниковые прослойки, которые в свою очередь являются активным препятствием для скольжения краевых дислокаций. Предложенный вариант закона упрочнения позволяет получить результаты, согласующиеся с экспериментальными данными.

103

Разработан и реализован алгоритм для определения на- пряженно-деформированного состояния поликристаллического агрегата. С использованием модели рассмотрены процессы одноосного нагружения, стесненной осадки. Приведены описание и анализ полученных численных результатов с учетом упрочнения и ротации решетки. Исследовано влияние сложности нагружения на характер деформирования (упрочнение и ротация решетки на мезоуровне, объемная доля двойников и т.д.).

Список литературы

1.Трусов П.В., Ашихмин В.Н., Швейкин А.И. Двухуровневая модель упругопластического деформирования поликристаллических материалов // Механика композиционных мате-

риалов и конструкций. – 2009. – Т. 15. – № 3. – С. 327–344.

2.Трусов П.В., Швейкин А.И. Теория пластичности: учебное пособие. – Пермь: Изд-во Перм. гос. техн. ун-та, 2011. – 419 с.

3.Трусов П.В., Волегов П.С. Физические теории пластичности: теория и приложения к описанию неупругого деформирования материалов. Ч. 2: Вязкопластические и упруговязкопластические модели // Вестник ПНИПУ. Механика. – 2011. – № 2. –

С. 101–131.

4.Трусов П.В., Нечаева Е.С., Швейкин А.И. Применение несимметричных мер напряженного и деформированного состояния при построении многоуровневых конститутивных моделей материалов // Физическая мезомеханика. – 2013. – Т. 16. –

№2. – С. 15–31.

104

СВЯЗАННАЯ МОДЕЛЬ СВС-ЭКСТРУЗИИ КОМПОЗИЦИОННОГО МАТЕРИАЛА

И.В. Механич, А.Г. Князева

(Национальный исследовательский Томский политехнический университет, Томск)

Впоследнее время все большее внимание уделяется освоению в промышленности новых технологий, которые направлены на получение конструкционных металлических и керамических композиционных материалов с нанофазной и нанокристаллической структурой. Использование таких материалов дает долгосрочный энерго- и ресурсосберегающий эффект, позволяющий значительно повысить экономическую эффективность производства, ресурс работы ответственных деталей и узлов машин и механизмов по сравнению с металлическими изделиями аналогичного назначения.

Ктаким новым технологиям непременно относится СВС (самораспространяющийся высокотемпературный синтез). Сущность СВС заключается в проведении экзотермических реакций в режиме распространения волны горения с образованием продуктов горения в виде соединений и материалов, обладающих ценными физикомеханическими характеристиками.

При оптимизации экспериментальных схем процессов экструзии весьма эффективным оказывается математическое моделирование. Оно позволяет, с одной стороны, прогнозировать результаты эксперимента, а с другой стороны, дает возможность выбрать оптимальные режимные факторы и наилучшие условия протекания процесса экструзии.

Вданной работе представлена одномерная модель СВСэкструзии, учитывающая эволюцию поля температуры, кинетику химического превращения, течение материала на основе обобщенной модели вязкой среды, граничные и начальные условия. В отличие от известных работ [1–4] в модели учитываются явления теплового и концентрационного расширения.

105

Список литературы

1.Неустойчивые режимы деформирования при твердофазной экструзии вязкоупругих структурированных систем / Н.А. Беляева, А.М. Столин, Д.В. Пугачев, Л.С. Стельмах // ДАН. – 2008. – Т. 420, № 6. – С. 777–780.

2.Беляева Н.А., Столин А.М., Стельмах Л.С. Динамика твердофазной экструзии вязкоупругого материала // Теоретические основы химической технологии. – 2008. – № 5. – С. 579–589.

3.Стельмах Л.С., Жиляева Н.Н., Столин А.М. Реодинамика и теплообмен горячего компактирования порошковых мате-

риалов // ИФЖ. – 1992. – Т. 63, № 5. – С. 612–622.

4.Смоляков В.К., Лапшин О.В. Формирование макроскопической структуры продукта в режиме силового СВС-компак- тирования // Физика горения и взрыва. – 2002. – Т. 38, № 2. –

С. 26–35.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА СОЗДАНИЯ КОМПОЗИЦИОННЫХ ЭЛЕКТРОХИМИЧЕСКИХ НАНОПОКРЫТИЙ

Е.К. Молчанов

(Институт механики УрО РАН, Ижевск)

Процесс работы любых механизмов сопряжен с постоянным воздействием различных физико-химических явлений, както трение, коррозия, тепловые воздействия и др. Детали механизмов испытывают статические, циклические и динамические нагрузки. Зачастую эти явления протекают совместно, что приводит к значительному снижению прочности и стойкости деталей механизмов, а также увеличению износа их рабочих поверхностей. В частности, композитные электрохимические покрытия (КЭП) находят широкое применение в качестве износостойких покрытий, покрытий с низким коэффициентом трения, покрытий для инструментов с высокой твердостью, по-

106

крытий для абразивного инструмента. КЭП получают из суспензий, представляющих собой растворы электролита с добавками определенного количества высокодисперсного порошка. При наложении электрического тока на поверхности покрываемого предмета (катода) осаждаются металл (первая фаза, матрица) и частицы порошка (вторая фаза), которые цементируются матрицей. В качестве дисперсной фазы выступают частицы диамет-

ром от 4 до 800 нм оксидов Al2O3, ZrO2, TiO2, SiO2, и Cr2O3, раз-

личных аллотропных соединений С, карбидов SiC, WC, TiC, нитридов Si3N4 и множества других материалов. В качестве металлической матрицы выступают такие металлы, как Cu, Ni, Co, Cr, Zn, Ag, Fe, Au, и их сплавы.

Для определения оптимального диапазона изменения параметров процесса и успешной практической его реализации, понимания механизма создания КЭП, поскольку он в настоящее время досконально не изучен, разработана математическая модель, объединяющая массоперенос частиц и ионов электролита в объеме электролитической ванны и кинетику осаждения металлической матрицы Cu, а также адсорбцию наночастиц и ионов к поверхности катода. Массоперенос частиц и ионов электролита во время СЭО описывается уравнениями конвективной диффузии [1]. Получены результаты моделирования процесса совместного электрохимического осаждения (СЭО) системы Cu–Al2O3 на вращающийся цилиндрический электрод [2].

Работа выполнена при поддержке гранта РФФИ 11-03- 00571-а и Программы фундаментальных исследований ОЭММПУ РАН № 12 «Многоуровневое исследование свойств и поведения перспективных материалов для современных узлов тре-

ния» (проект 12-Т-1-1009).

Список литературы

1. Вахрушев А.В., Молчанов Е.К. Математическое моделирование процесса совместного электрохимического осаждения наночастиц Al2O3 в матрицу Cu. Ч. 1: Математическая мо-

107

дель // Химическая физика и мезоскопия. – 2013. – Т. 15, № 1. –

С. 57–64.

2. Вахрушев А.В., Молчанов Е.К. Математическое моделирование процесса совместного электрохимического осаждения наночастиц Al2O3 в матрицу Cu. Ч. 2: Расчет одномерного процесса осаждения // Химическая физика и мезоскопия. – 2013. –

Т. 15, № 2. – С. 50–57.

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТЕПЛОВОЙ КОНВЕКЦИИ В АППАРАТЕ ПОЛУЧЕНИЯ ТИТАНА

В.Н. Нечаев1, А.И. Цаплин2

(1Российиский научно-исследовательский

ипроектный институт титана и магния, Березники; 2Пермский национальный исследовательский политехнический университет, Пермь)

Втезисах доклада на школе-конференции за 2011 г. [1] излагалось, в частности, о том, что в современной хлорной металлургии титана широко применяется способ Кролля, т.е. восстановление тетрахлорида титана в расплаве магния при температурах 750...870 °С и избыточном давлении инертного газа 0,02...0,03 МПа. Процессы восстановления ведут в герметичных аппаратах (реакторах) цилиндрической формы, изготовленных из нержавеющей стали [2]. В отечественной промышленности для этих целей используются аппараты с цикловым съемом по титану от 3,5 до 7,0 т, имеющие значительные размеры: внутренний диаметр 1,55 и 1,70 м; длина от 3,60 до 4,30 м.

Для принятой геометрии аппаратов и организации технологического процесса важной практической задачей является изучение особенностей изменения температур в центре реактора или в любой его точке, скоростей полного прогрева аппарата, распределение температурных полей. Решение указанных во-

108

просов необходимо для оптимизации процесса восстановления. Таким образом, адекватное решение неравновесной задачи тепловой конвекции применительно к реальному объекту – аппарату для металлотермического получения титана – весьма актуально.

Постановка задачи тепловой конвекции заключается в следующем: аппарат восстановления, установленный в шахтную электропечь, рассматривается в цилиндрической осесимметричной двумерной системе координат. Расчетная область ограничена слева осью симметрии, справа – стенкой реторты, в нижней части – сварным швом крепления сферического днища к обечайке реторты, сверху – заглублением крышки в реторту. На оси симметрии – адиабатная граница. Для функции скорости на всех границах в зоне расположения расплава магния принято условие полного прилипания вязкой среды. В ходе решения уравнения переноса энергии была разработана специальная методика определения коэффициентов теплоотдачи, входящих в условия теплообмена на границах расчетной области.

Решение поставленной задачи было реализовано в математической модели, учитывающей гидродинамические явления в расплаве магния в соответствии с представленной полной постановкой задачи тепловой конвекции. Для проверки адекватности модель тестировалась первоначально в бесконвективном приближении, т.е. решалось отдельно уравнение переноса энергии, затем тестировалось решение сопряженной задачи с учетом конвективных составляющих в переменных завихренность– функция тока. Тестирование математической модели показало удовлетворительные результаты.

На данном этапе разработанная математическая модель и компьютерная программа позволяют анализировать неравновесные теплофизические процессы в аппарате для получения титана на этапе разогрева, когда реактор заполнен только жидким магнием. Пока не учтены подача тетрахлорида титана, образование побочного продукта взаимодействия – хлорида маг-

109

ния и формирование блока титановой губки. Учет гидродинамических явлений в расплаве магния позволил уточнить температурную обстановку, выявив концентрацию температурных градиентов у стенки реторты. Следующим этапом работы станет развитие модели с учетом фильтрации жидкой фазы через пористую среду осаждаемого губчатого титана.

Список литературы

1.Нечаев В.Н., Цаплин А.И. Математическая модель процесса термического восстановления в технологии производства губчатого титана // Математическое моделирование в естественных науках (ММЕН): тез. докл. ХХ Всерос. школы-конф. молодых ученых и студентов. – Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2011. – С. 67–68.

2.Титан / В.А. Гармата, А.Н. Петрунько, Н.В. Галицкий

[и др.]. – М.: Металлугия, 1983. – 559 с.

МУЛЬТИФРАКТАЛЬНЫЙ АНАЛИЗ БИОЛОГИЧЕСКИХ СИСТЕМ НА ОСНОВЕ ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ

А.С. Никитюк, О.Б. Наймарк

(Институт механики сплошных сред УрО РАН, Пермь)

В настоящее время значительное внимание обращается на структурные аспекты поведения биологических систем на разных масштабных уровнях с целью объяснения основных механизмов функционирования ДНК, клеточных и надклеточных структур, биологических тканей. Понимание данных механизмов позволит объяснить с физической точки зрения процессы деградации биологических систем живых организмов, в частности развитие раковых опухолей. На данный момент существует обширная база клинических данных, на основе которых можно провести детальное исследование данного вопроса. В связи

110