723

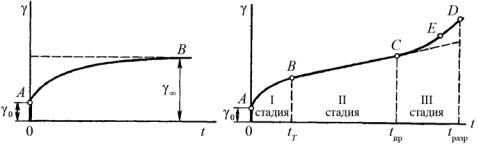
вившуюся и прогрессирующую. Такой вид кривых ползучести типичен для самых различных глинистых грунтов – от текучей до твердой консистенции независимо от вида испытаний: на сдвиг, одноосное и трехосное сжатие и т.д.

Рис. 3.9. Кривые изменения во времени деформации: а – затухающая ползучесть; б – незатухающая ползучесть

Всем грунтам, начиная от слабых глинистых и кончая скальными, свойственны общие реологические закономерности. В зависимости от величины нагрузки, типа грунта и вида напряженного состояния могут развиваться затухающая ползучесть, заканчивающаяся стабилизацией деформации, «вековая» ползучесть, при которой скорость деформации затухает, тогда как сама деформация неограниченно нарастает, не приводя, однако, к разрушению, условно-установившаяся ползучесть в виде пластично-вязкого течения и, наконец, прогрессирующая ползучесть, приводящая к разрушению. Превалирование той или иной стадии ползучести и их удельная роль существенно зависят от типа грунта. Н.К. Пекарская (см.: Прочность мерзлых грунтов при сдвиге, ее зависимость от текстуры. М., 1963), проделавшая интересный анализ закономерностей поведения грунтов в зависимости от характера структурных связей, установила, что именно вид этих связей и определяет в первую очередь характер процесса деформирования. Так, пластичным глинам с преимущественными водно-коллоидными связями (коагуляционные структуры) свойственны все стадии деформирования, характерные для классической кривой ползучести. При этом чем пластичнее грунт, тем скорее наступает стадия установившегося течения и тем большую роль она играет в процессе деформирования. У грунтов текучей консистенции эта стадия является доми-

111

нирующей, и эти грунты по своим свойствам приближаются к вязкой жидкости. Стадия прогрессирующего течения у пластичных грунтов с водно-коллоидными связями возникает при нагрузках, составляющих 40–70 % от кратковременной прочности, и развивается длительное время, заканчиваясь разрушением, как правило, вязким [27].

Уплотных глинистых грунтов со смешанными коагуляционными

икристаллизационными связями преобладает стадия затухающего деформирования. Прогрессирующая стадия возникает при нагрузках, составляющих 70–80 % и более от кратковременной прочности, причем переход от затухающего к прогрессирующему деформированию наблюдается в большинстве случаев без стадии установившегося течения. При этом относительная продолжительность прогрессирующей стадии невелика, а разрушение бывает преимущественно хрупким.

Аналогичные закономерности характерны и для полускальных

ислабых скальных пород с кристаллизационными связями. Однако для этих пород определяющую роль играет характер цементирующих связей. Если цементное вещество обладает выраженными реологическими свойствами, то эти свойства будут проявляться и у всей породы

вцелом. Типичным примером такой породы является мерзлый грунт,

укоторого роль цементирующего вещества играет лед – материал, представляющий собой образец классического нелинейно-вязкого тела. Соответственно поведение мерзлого грунта отображается типичными кривыми ползучести со всеми стадиями, свойственными этому процессу для классических ползучих сред, и с переходом в прогрессирующую стадию при нагрузках, величина которых может составлять всего 10–25 % от мгновенной прочности. Отметим, что у металлов при высокой температуре незатухающая ползучесть, как правило, начинается под воздействием самой малой нагрузки.

Другим примером скальной породы с вязким цементирующим веществом служат песчаники с глинистым цементом. Вязкие свойства глинистого цемента выражены, однако, в значительно меньшей степени, чем у льда. Поэтому у такой породы доминирует стадия затухающего деформирования, тогда как установившаяся стадия или невелика, или вообще отсутствует. Прогрессирующая стадия в таких песчаниках возникает лишь при очень больших нагрузках.

Породы, у которых цементирующее вещество обладает малыми вязкими свойствами, приближаются по своему поведению к хрупким

112

телам. Однако здесь надо учитывать свойства самих кристаллов породы. Известно, что для кристаллов с преимущественно ковалентными связями пластические деформации, обусловленные скольжением атомных слоев монокристалла, затруднены. Для таких кристаллов характерны только упругие деформации и хрупкое разрушение [27].

Кристаллы с ионными связями ведут себя хрупко при быстром приложении нагрузок, но обнаруживают вязкие свойства при длительном воздействии нагрузок. Примером является каменная соль, свойства ползучестикоторойбылиустановленыещевопытах Вейнбергав1903 г.

В заключение отметим, что для всех рассмотренных грунтов развивающиеся во времени деформации играют основную роль: они значительно превышают мгновенные деформации: в одних случаях в 2– 10 раз, а в других в десятки и сотни раз [27].

Ползучесть скелета грунта. Ползучесть глинистых грунтов является следствием не только наличия водных пленок, окружающих твердые частицы. Конечно, эти пленки, обладающие явно выраженными вязкими свойствами, существенно способствуют развитию реологических процессов в водонасыщенных дисперсных грунтах с вод- но-коллоидными связями. Однако и конденсационные связи между минеральными частицами при «сухом» контакте, обусловленные межмолекулярными силами ближнего действия, оказывают вязкое сопротивление смещению частиц. Соответственно грунты с таким видом связей обладают свойствами ползучести (рис. 3.10).

Рис. 3.10. Кривые ползучести высушенного глинистого грунта при сжатии в одометре без возможности бокового расширения:

1 – в высушенном состоянии; 2 – после увлажнения

113

Песок тоже обладает свойством ползучести – деформация уплотнения у него развивается во времени, подчиняясь логарифмическому закону (рис. 3.11).

Рис. 3.11. Кривые ползучести мелкозернистого песка при сжатии в одометре без возможности бокового расширения

Свойство текучести песка известно из повседневной практики: вытекание песка из отверстия под действием гравитационных сил (песчаные часы), движение барханов в пустыне и т.д. Песок представляет собой как бы крупномасштабную модель хаотически расположенных и слабо между собой связанных молекул жидкости и аналогично ей подчиняется статистическому закону вязкого течения. Но, конечно, этот процесс протекает у песка в значительно менее выраженной форме, чем у дисперсных грунтов.

3.1.9.Методика обработки опытных данных

Вестественных условиях реологические процессы в грунтах развиваются десятки и сотни лет. В лабораторных же условиях мы ограничены техническими возможностями и можем проводить опыты в течение нескольких часов и дней, реже – месяцев и совсем редко – лет. Вследствие этого приходится данные кратковременных испытаний грунтов экстраполировать на длительные отрезки времени. Естественно, что к такой экстраполяции надо подходить очень осторожно [27].

Оценка реологических свойств грунта по данным испытаний на ползучесть заключается в выборе эмпирического уравнения ползуче-

114

сти и в определении параметров этого уравнения. Применяя принятое уравнение ползучести при известных из опытов параметрах, можно прогнозировать поведение грунта, используемого как основание или как материал сооружения, во времени. Естественно, что экстраполяция данных лабораторных испытаний на сроки, которые на несколько порядков превышают продолжительность испытания, требует тщательной обработки и анализа этих данных.

Испытания грунта на ползучесть обычно проводят или с серией образцов, к каждому из которых прикладывают постоянную (но различную для каждого образца) нагрузку, или один образец загружают нагрузкой, увеличиваемой ступенями, выдерживаемыми в течение некоторого интервала времени ∆t. Этот интервал принимают или постоянным для всех ступеней, или таким, чтобы на каждой ступени нагрузки в стадии затухающей ползучести деформации достигли условной стабилизации. По результатам испытаний строят семейство кривых ползучести и соответствующее им семейство изохронных кривых (рис. 3.12) [27].

Рис. 3.12. Изохорные кривые (а), кривые ползучести (б), приведение их к единым кривым (в, г)

Для однородной изотропной среды теоретически считается справедливым закон наложения деформаций Больцмана. Это означает, что

115

деформацию ползучести от действия некоторой переменной во времени нагрузки можно определить путем суммирования деформаций, вызванных действием элементарных приращений напряжения.

При проведении испытаний грунтов и определении их характеристик получается большой разброс опытных данных, что связано с неоднородностью грунтов, нарушением их естественного сложения и изменением свойств при отборе образцов и погрешностью самих опытов. Этот разброс столь велик, что различие в значениях полученных данных в пределах 10–20 % считается удовлетворительным и даже хорошим совпадением, а в 5 % – малоправдоподобным. Поэтому обработку опытных данных следует вести методами математической статистики [27].

Выбор того или иного уравнений ползучести сводится к тому, чтобы на основании опытных данных подобрать эмпирическую формулу, которая лучше всего описывает опытную кривую. Для этой цели обычно применяют метод выравнивания опытной кривой, заключающийся в построении графика в таких координатах, в которых рассматриваемая кривая преобразуется в прямую. Так, если имеется некоторая нелинейная зависимость

то для ее преобразования в уравнение прямой надо ввести новые переменные X, Y, отвечающие условиям:

и подобрать функции φ1 и φ2 так, чтобы величины X и Y были связаны линейной зависимостью

В этом случае и с учетом нормального (гауссова) закона распределения ошибок параметры В и D находят из совместного решения двух уравнений, называемых нормальными:

где n – число экспериментальных точек.

Из решения этого уравнения легко определить значения параметров В и D:

116

Поскольку в формулы (3.11г) входят разности больших чисел, вычисления надо вести с большой степенью точности, избегая округления результатов промежуточных подсчетов.

3.2. Базовые реологические теории

3.2.1. Теории ползучести

Теория линейного упруговязкого деформирования. Теория линей-

ного упруговязкого деформирования исходит из рассмотрения совместного проявления упругих и вязких свойств тела. Впервые уравнение упруговязкости было сформулировано Максвеллом для описания явления релаксации, затем Кельвин и Фойгт предложили уравнения последействия. В общем виде такое уравнение имеет вид

где α0 = –τ – предельное напряжение сдвига по Бингаму; α1 = 1; α2 =

=Tr = η/G0 – время релаксации; β2 = η – коэффициент вязкости; β1 =

=G∞, причем G0 и G∞ – мгновенное и предельно-длительное значения

модуля cдвига.

Реологические уравнения состояния связывают напряжение, деформацию, ее скорость и время (в явной или неявной форме). Вид связи определяется той или иной принятой гипотезой, в зависимости от которой и различают теории ползучести [27].

Механические модели. В теории линейной упруговязкости широко распространен метод модельного отображения реологических свойств тела, исходящий из представления, что эти свойства определяются сочетаниемупругих, вязкихипластическиххарактеристик(рис. 3.13).

Упругие свойства тел отображают моделью в виде упругого элемента (пружины), подчиняющегося закону Гука τ = Gγ и обозначаемого символом Н. Вязкие свойства тел отображают моделью в виде

117

цилиндра, наполненного жидкостью, в которую погружается дырчатый поршень, причем скорость погружения описывается законом Ньютона τ = ηγ; этот элемент обозначают символом N. Пластические свойства отображаются элементом сухого трения, подчиняющимся закону Сен-Венана τ = τт,

где τт = τs – напряжение, до пре-

вышения которого деформация не возникает; этот элемент обозначают символом SV.

Последовательное соединение указанных элементов обозначают через тире (например, Н–N), а параллельное – вертикальной чертой (например, H|N). Очевидно, что указанные три элемента можно соединять в самых различных сочетаниях; эти сочетания и будут описывать различные проявления упруговязких свойств тела. Модельные представления свойств тела, подкупающие своей наглядностью и простотой, получили широкое распространение. И нет, пожалуй, ни одной книги по вопросам реологии, в которой не приводились бы механические модели упруговязких тел [29].

Вместе с тем многочисленные опыты с различными материалами показали, что модельные представления и вытекающие из них уравнения деформирования не дают хорошего совпадения с действительным поведением этих материалов. Это и естественно, поскольку никакие модели – ни в их простейшем виде, ни в виде самых сложных комбинаций, к которым прибегают некоторые авторы, – не могут отобразить реальные свойства тела.

Если же использовать модели для рассмотрения только качественной стороны процесса, то, учитывая наглядность этого метода, он может представить определенный интерес. Исходя из этих соображений, а также для полноты представления о реологических теориях в их историческом развитии рассмотрим основные модели упруговязких тел.

Тело Кельвина–Фойгта – тело, обладающее свойством последействия, но не проявляющее свойства релаксации (рис. 3.14, а).

118

рому деформация в какой-либо момент времени t, вызванная нагрузками, приложенными в предшествующие моменты v, равна сумме деформаций, которые развились бы ко времени t, когда каждая из нагрузок действовала бы независимо от других. Иными словами, деформация в данный момент зависит не только от величины напряжения, действующего в этот момент, но и от истории предшествующего деформирования, как бы наследуя влияние действующего ранее напряжения. Отсюда произошло и название теории.

Пусть в момент времени v к телу приложена нагрузка τ(v), действующая в течение небольшого интервала времени v и вызвавшая деформацию y(v). Деформация в произвольный момент времени t > v будет пропорциональна напряжению τ(v), длительности его действия v и некоторой функции K(t – v), зависящей от свойств тела и от промежутка времени t – v, прошедшего с момента v приложения нагрузки по момент t, для которого определяется деформация y(t). Если, кроме того, в рассматриваемый момент t на тело действует изменяющееся во времени напряжение τ(t), то оно вызовет мгновенную деформацию γ = τ(t)/G0 где G0 – мгновенный модуль упругости [27]. Исходя из ска-

занного, полная деформация в момент времени t > v

Соотношения (3.14) и (3.15) являются интегральными уравнениями Вольтерры второго рода. Соотношение (3.15) есть решение уравнения (3.14) относительно τ, и, наоборот, соотношение (3.14) – решение уравнения (3.15) относительно γ.

Ядра интегральных уравнений K(t – v) и R(t – v) есть функции двух переменных: t и v. При этом функция R(t – v) – ядро релаксации – явля-

120