Квалиметрические модели методы и алгоритмы контроля дешифрации и оц

В модели простого теста неопределенности при локализации значения выходной переменной нет, так как нет области наложения функций при-

надлежности разных термов. Далее перейдем к моделям более сложных

тестов, контролирующих несколько ЭДК.

Применение нечеткого вывода для дешифрации результатов сложного теста. Построим модель для сложного теста, контролирующего

два ЭДК: Э1 и Э2. Универсальное множество в данном случае представляет собой совокупность результатов тестирования в виде оценки О(Т), нормализованной в диапазоне [0; 1] и обозначаемую далее также через Т.

Выходной лингвистической переменной является информация об уровне освоения всех контролируемых ЭДК S, определяемая количеством неосвоенных ЭДК (нЭДК). Она может быть выражена через терм-множество, состоящее из трех термов: {«оба ЭДК не освоены» (S2); «один из ЭДК не освоен» (S1); «все ЭДК освоены» (S0)}. Варианты значений выходной лингвистической переменной могут быть представлены в табличном виде через все варианты сочетаний значений уровня освоения каждого из контролируемых ЭДК (табл. 3.2). В табл. 3.2 приняты следующие условные обозначения: 0 – ЭДК не освоен, 1 – ЭДК освоен.

В общем случае из множества, содержащего h проверяемых тестом

ЭДК, i элементов могут быть не освоены, а (h – i) – освоены. Поэтому

оценка за тест О при i неосвоенных ЭДК – О(i) – с учетом введенных ограничений и допущений строится в соответствии с аддитивным интегродифференциальным критерием, при фиксированных значениях h и Опор –

была введена по (2.15).

Можно сделать вывод, что граничные значения оценки при заданном количестве нЭДК (i) определяются общим числом равнозначных ЭДК h

и пороговым значением принятия решения Опор. Граничные оценки будут использованы для задания логических условий при дешифрации результа-

тов проверки.

Функция принадлежности для каждого значения выходной переменной характеризует степень принадлежности, может быть представлена линейной зависимостью и описана следующим образом:

101

Представим функции принадлежности на графике (рис. 3.2). Характеристики функций принадлежности подтверждаются моделированием всех возможных сочетаний значений уровней освоения каждого из контроли-

руемых ЭДК.

Применение аппарата нечеткой логики позволяет сделать четкие вы-

воды при решении задач дешифрации результатов реализации совокупно-

сти тестов, проверяющих уровень освоения набора элементов дисциплинарных компетенций. Также возможно избежать компенсации оценок на любом уровне иерархической модели результатов обучения (интегральный показатель подготовленности – компетенции – дисциплинарные компетенции – компоненты дисциплинарной компетенции – элементы компонентов дисциплинарной компетенции). Предложенные подходы эффек-

тивно алгоритмизируются и могут быть использованы в составе информационного и программного обеспечения автоматизированной системы сопровождения учебного процесса.

3.2. Разработка метода дешифрации результатов тестового диагностирования с использованием нечеткой логики

Для современной системы образования России актуальными и значимыми являются проблемы контроля и оценки результатов обучения, заданных в компетентностном формате. Однако задачи дешифрации резуль-

102

татов тестового диагностирования имеют неопределенность в принятии решения, возникающую из-за компенсации одних результатов другими в составе применяемого аддитивного интегро-дифференциального критерия оценки (АИДКО). Поэтому для обработки и дешифрации результатов тестового диагностирования уровня освоения компетенций и их составляющих (компонентов и элементов) было предложено применение аппарата нечеткой логики. В данном разделе предлагается построенный с использованием аппарата нечеткой логики алгоритм дешифрации результатов проверки с использованием сложных тестов, контролирующих несколько ЭДК, и приводится развернутый иллюстрирующий пример.

Наличие одного теста не дает возможности сделать четкий вывод (вы-

полнить дефаззификацию) из-за вероятности возникновения компенсации

высоких оценок низкими и наоборот. В практике применения нечеткой логики значение переменной дополняют, например, значением ее производной [135]. В нашем случае дополним использование одного теста другим, пересекающимся по одному из контролируемых элементов [127].

Дешифрация результатов реализации совокупности сложных тестов с применением аппарата нечеткой логики. Пусть тест Т1 контроли-

рует элементы Э1 и Э2, а тест Т2 – элементы Э2 и Э3 (пересечение тестов по элементу Э2). Для каждого из них проводится фаззификация и определяются функции принадлежности. Размерность каждого терм-множества

равна максимальному количеству возможных значений неосвоенных ЭДК (нЭДК) – (hj + 1), где hj – количество ЭДК, контролируемых тестом Тj. По-

этому общее количество продукционных правил, в каждом из которых по выполнению условий вида (IF ... THEN ...) принимается решение о значении выходной переменной [12], определяется как произведение размерно-

стей всех терм-множеств: (h1 + 1) (h2 + 1) = (2 + 1) (2 + 1) = 9.

Выходная лингвистическая переменная принимает значения, определяемые числом сочетаний состояний («освоен»/«не освоен») для каждого

из h контролируемых всей совокупностью тестов элементов, т.е. 2h. Поскольку в нашем случае h = 3 (Э1, Э2, Э3), общее количество вариантов значений (состояний) выходной переменной определяется как 2h = 23 = 8 и может быть представлено в табличном виде (табл. 3.3). Значения выходной переменной S зададим в виде десятичного числа, соответствующего двоичному коду, характеризующему состояние освоения элементов (0 – ЭДК не освоен, 1 – ЭДК освоен).

Таким образом, значения выходной переменной задаются термами с функциями принадлежности в виде синглетонов (только значения = 1) (рис. 3.3).

103

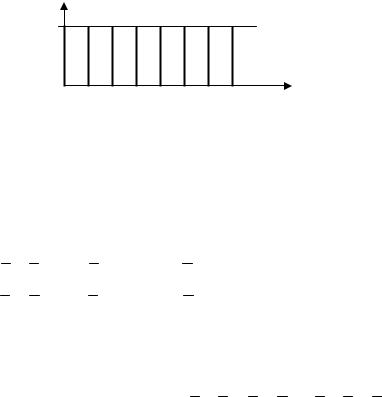
Таблица 3 . 3 Варианты и значения выходной лингвистической переменной

(S)

1

Рис. 3.3. Функции принадлежности выходной переменной

Запишем продукционные правила. Для этого предлагается ввести логическое описание (L) каждого элемента терм-множества через булевы функции:

для Т1: L2 Э1 Э2 , L1 Э1 Э2 Э1 Э2 , L0 Э1 Э2 ,

для Т2: L2 Э2 Э3,L1 Э2 Э3 Э2 Э3,L0 Э2 Э3.

Тогда значение выходной переменной S в каждом правиле будет определяться как логическое произведение выражений для соответствующих термов (L = L1·L2) из табл. 3.3.

1. IF Т1 S2 AND Т2 S2 THEN L Э1 Э2 Э2 Э3 Э1 Э2 Э3; S 0:

если результаты обоих тестов принадлежит интервалу S2, то выходная пе-

ременная S = 0, что соответствует решению о том, что все контролируемые ЭДК не освоены.

104

Примечание. * – результат не может быть получен; правило не используется; ** – результат не может быть определен; правило записывается в обоих вариантах.

Совокупность всех правил удобно представить в виде матрицы решений. В ней столбцы соответствуют условиям одного параметра T1, а строки – условиям другого параметра T2. На пересечении столбцов и строк за-

писываются выводы, соответствующие указанным условиям (табл. 3.4).

Таблица 3 . 4 Матрица решений

Далее предлагается алгоритм решения задачи дешифрации результатов реализации совокупности тестов с использованием дефаззицикации (по

методу, предложенному Л. Заде [135]).

1.По заданным значениям результатов тестов определяются значения степеней принадлежности (значение функции принадлежности терма для заданного значения универсума, т.е. результат соответствующего теста)

для всех термов.

2.Выбираются правила, содержащие условия с ненулевыми степеня-

ми принадлежности (термы, которым соответствуют ненулевые значения функций принадлежности для заданных конкретных результатов тестов).

3.На первом шаге логического вывода определяется степень принадлежности всего антецедента каждого правила (по функции минимума).

105

4.На втором шаге формирования нечеткого вывода определяет-

ся степень принадлежности терм выходной переменной (по функции максимума).

5.Для дефаззификации применяется метод центроида, который позволяет определить текущее значение выходной переменной для текущих значений лингвистических переменных. В результате определяется четкий результат, дающий информацию об уровне освоения каждого из контролируемых всей совокупностью тестов ЭДК.

Пример 3.1. Пусть тест Т1 контролирует элементы Э1 и Э2, а тест Т2 – элементы Э2 и Э3 (пересечение тестов по элементу Э2). После реализации теста (тестирования студента) получены следующие результаты, которые

будут использовать в качестве исходных данных для расчета по предло-

женному алгоритму: Т1 = = 0,375; Т2 = 0,375. Примем Опор = 0,5.

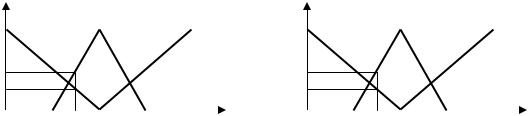
Функции принадлежности аналитически описываются следующими выражениями и графически (рис. 3.4):

1. Для заданных значений результатов тестов определим функции принадлежности:

2. Выберем сформулированные выше продукционные правила, которые имеют ненулевую степень принадлежности: 1, 2, 4, 5 (см. рис. 3.4).

106

3. На первом шаге логического вывода необходимо определить степень принадлежности всего антецедента (логическое условие) каждого правила для S(Т), S = 0,...,7 (табл. 3.3):

Правило 1: 0 (Т) min{ S2 (Т1); S2 (Т2 )} min{0,25;0,25} 0,25;

2 (Т) min{ S1 (Т1); S1 (Т2 )} min{0,5;0,5} 0,5.

4.Второй шаг формирования нечеткого вывода для определения степени принадлежности терм выходной переменной в настоящем примере выполнять не нужно, так как все выходные переменные участвуют в выводе по одному разу. При данном состоянии входных переменных степень принадлежности терма выходной переменной S имеют следующие значения:

{ 0; 1; 2; 3; 4; 5; 6; 7} {0,25;0,25;0,5;0;0,25;0,5;0;0}.

5. Для перехода от нечетких выводов к четким выводам используем метод центроида:

SS0 0 S1 1 S2 2 S3 3 S4 4 S5 5 S6 6 S7 7

0 1 2 3 4 5 6 7

0 0,25 1 0,25 2 0,5 3 0 4 0,25 5 0,5 6 0 7 0 2,7. 0,25 0,25 0,5 0 0,25 0,5 0 0

Поскольку выходное значение находится между значениями выходной переменной S = 2 и S = 3, а значения S = 3 нет в списке выходных переменных выбранных продукционных правил, то принимается решение о значении выходной переменной S = 2. Это соответствует состоянию

Э1 & Э2 & Э3 (табл. 3.3).

Применение аналитической модели весьма трудоемко даже для решения задач дешифрации небольшой размерности. Поэтому необходима автоматизация процедуры дешифрации и оценивания. Далее предлагается вариант реализации предлагаемых подходов и алгоритмов в среде модели-

рования MatLab, пакет Fuzzy Logic (рис. 3.5).

Результат эмуляции в выбранной среде моделирования для исходных данных из примера 1 практически совпадает с результатами аналитического моделирования (небольшие отличия из-за разных способов дефаззификации – Заде и Мамдани). Это позволяет сделать вывод о возможности использования предлагаемых алгоритмов при дешифрации и оценивании результатов тестового диагностирования.

107

Рис. 3.5. Реализация модели в среде MatLab Fuzzy Logic

3.3. Применение нечеткой логики для определения интегральных оценок результативности подготовки

Задача определения интегральной оценки результатов обучения на основе дифференциальных (частных) оценок может иметь значительную размерность (при большом количестве дифференциальных оценок и многоуровневой шкале) и сложность (из-за необходимости сформулировать и формализовать большое количество правил). Поэтому эффективным решением является автоматизация определения количественной оценки интегрального показателя. В основе формализации решения указанной задачи лежит выбор аппарат формальной логики. Автором было исследовано применение двух аппаратов: математической и нечеткой логики.

108

Каждый аппарат имеет свои достоинства, ограничения и область целесообразного применения. Достоинство детерминированной логики – в возможности сформулировать и строго рассчитать результаты применения продуктивных правил (логических условий) с использованием, например, булевой или недвоичной алгебры для дешифрации диагностических таблиц. При этом возможно использование многоуровневых шкал с равномерным или неравномерным распределением интервалов между соседними уровнями. Достоинство нечеткой логики – возможность применения многоуровневых шкал, важность уровней в которых задается функциями принадлежности, выбираемыми по согласованию с заказчиком. Также за счет введения дополнительных градаций (например, в виде «+» и «–») и последующей дефаззификации (преобразования нечеткого множества

вчеткое число) появляется возможность перехода от векторной оценки к скалярной.

Далее рассмотрим применение только нечеткой логики для решения поставленной задачи – определение интегральной оценки результатов государственного экзамена (использование детерминированной логики – параллельное направление исследований, проводимых автором). Отметим, что предлагаемый подход является инвариантным к виду и форме аттестационных испытаний и может быть использован для принятия решения

вмногокритериальных задачах.

3.3.1. Аналитическая модель решения задачи при использовании методов нечеткой логики

Входными лингвистическими переменными являются дифференциаль-

ные оценки, для рассматриваемого примера ГЭ – оценки за решение задачи (Z) и ответы на вопросы (Q1, Q2, Q3); выходной лингвистической переменной будем считать интегральную (итоговую) оценку (I). Терммножество для каждой лингвистической переменной содержит описание уровней выбранной шкалы оценивания размерности N ({Li, i [1; N]}). Например, для N = 4, {Li, i [1; 4]} = {«отлично»; «хорошо»; «удовлетворительно»; «неудовлетворительно»} или {«2», «3», «4», «5»}.

Термам могут быть заданы различные функции принадлежности относительно количественных значений оценки, например, в виде синглетона или треугольной (рис. 3.6).

Универсальное множество (универсум) в данном случае представляет собой количественное значение (точечное или интервальное – в зависимости от выбранной функции принадлежности) оценки за решение задачи или ответ на вопрос. Например, описание функции принадлежности вида синглетон и треугольной формы μ(Tj), где Tj – терм, имеет следующий вид:

109

Рис. 3.6. Пример функций принадлежности

Параметры шкалы (количество термов входных/выходных переменных):

–размерность N (количество уровней);

–шаг квантования (интервал между уровнями):

•постоянный;

•переменный;

–взаимное расположение функций принадлежности соседних термов (для функций принадлежности треугольного вида, рис. 3.7):

ивыходных лингвистических переменных

•Li max < L(i+1) max: функции принадлежности соседних термов не соприкасаются (без неопределенности вывода);

110