Теория определяющих соотношений. Часть 1. Общая теория

41

Кроме того, поскольку эволюционные уравнения описывают фундаментальные физические механизмы, реализуемые в широком классе реальных материалов, модели данного типа обладают значительной универсальностью. К основным недостаткам рассматриваемого подхода следует отнести: большое число внутренних переменных и соответствующих эволюционных уравнений, необходимых для адекватного описания процесса необратимого деформирования; трудности в решении «проблемы замыкания»; отсутствие в подавляющем большинстве случаев аналитических решений системы эволюционных и определяющих соотношений, что приводит к необходимости использования численных методов.

Следует отметить, что, с учетом приведенного выше определения внутренних переменных, в настоящее время невозможно назвать какуюлибо теорию необратимых деформаций, не использующую – явно или неявно – эти переменные. Например, в классической теории пластичности широко применяется понятие поверхности текучести, отделяющее в пространстве напряжений (или деформаций) области упругого и неупругого деформирования. В процессе деформирования поверхность текучести изменяет свою форму и размеры, перемещается как целое. Эта эволюция поверхности текучести отражает изменение свойств материала, обусловленное изменением мезо- и микроструктуры, в связи с чем параметры, описывающие эволюцию этой поверхности, с полным правом можно отнести к внутренним переменным. Аналогичная ситуация имеет место и в других теориях (вязкоупругости, вязкопластичности, ползучести и др.).

В связи с вышесказанным в структуре ОС, описывающих процессы необратимого деформирования, должны фигурировать внутренние переменные. В качестве последних будут использоваться тензорзначные пере-

менные Jβ , β = 1, B (произвольной в общем случае валентности); вопрос о

типе, физическом смысле и аргументах внутренних переменных решается в рамках конкретных теорий ОС.

Следует отметить, что часть внутренних переменных непосредственно входит в структуру ОС данного масштабного уровня, такие пере-

менные в дальнейшем будем обозначать Jβe , β = 1, Be и для ясности назы-

вать их внутренними «явными» (explicit) переменными. К числу таких переменных относятся, например, параметры, характеризующие форму, положение и размеры поверхности текучести в теориях пластического течения.

Вообще говоря, к переменным данного типа следует отнести также упругие и пластические составляющие тензора «полных» деформаций в упругопластических телах. Действительно, эти составляющие, безусловно, отражают структурные перестройки материала; в ряде физических моделей, появившихся в последние годы, для их определения используют мик-

42

ро- и мезоскопические характеристики материала и процесса нагружения (деформирования). Тем не менее в настоящем изложении будем следовать традициям МСС, относя эти переменные к параметрам воздействия (или отклика) и используя известные соглашения об определении упругих составляющих из закона, описывающего разгрузку, и аддитивный или мультипликативный способ разложения деформаций на упругие и пластические составляющие.

Вторая группа внутренних переменных (в большинстве случаев относящихся к более глубоким масштабным уровням) входит в качестве переменных в эволюционные уравнения (ЭУ); переменные этой группы бу-

дем обозначать как Jβi , β 1, i ; для того чтобы отличать их от перемен-

ных первой группы, будем называть их внутренними «скрытыми (неявными)» (implicit) переменными. К числу таких переменных в теориях неупругого деформирования поликристаллов (мезо- и макроуровней) можно отнести, например, плотность краевых и винтовых дислокаций. Полная совокупность внутренних переменных, таким образом, определяется как

Введенные выше параметры Pα в зависимости от контекста могут

содержать все или часть мер, характеризующих напряженное и деформированное состояние исследуемого тела. Учитывая, что ОС в общем случае представляют собой ограничения (связи), накладываемые на параметры всех типов, ОС в достаточно общей форме может быть записано следующим образом:

Π(Pα ,Jeγ ) 0 .

Наиболее употребительными в МСС являются уравнения состояния, записанные в разрешенном относительно напряжений виде,

Определяющие соотношения (17) или (18) должны быть дополнены еще двумя группами соотношений – эволюционными и замыкающими. О второй группе будет сказано ниже. К эволюционным уравнениям, в отличие от традиционно принятых, здесь относятся соотношения только для

Jiδ можно описать следующими эволюционными (кинетическими) уравне-

ниями, которые можно записать разрешенными в терминах или самих внутренних переменных, или их объективных производных:

Замечание. Одной из наиболее сложных проблем теории определяющих соотношений (ТОС) является проблема замыкания эволюционных и определяющих уравнений (наиболее известным примером может служить проблема замыкания в теории турбулентности). Суть проблемы состоит в том, что при формулировке физических уравнений, особенно в случае необходимости описания эволюции микроструктуры, для представительного макрообъема возникает необходимость введения параметров меньшего масштабного уровня и эволюционных уравнений для них, и так далее – вниз по «лестнице масштабов». В некоторых теориях, например, в теории пластического течения, удается замкнуть систему физических уравнений на рассматриваемом масштабном уровне (для теории пластического течения – введением функции текучести или пластического потенциала, зависящих от изменяемой микроструктуры). «Платой» за подобное замыкание является проведение весьма трудоемких и дорогостоящих экспериментов. В связи с этим в последние 10–15 лет интенсивно развиваются подходы к построению физических уравнений, основанные на иерархических моделях нескольких масштабных уровней.

В настоящее время в механике сплошной среды (МСС), микро- и мезомеханике наиболее употребительным является использование четырех масштабных уровней: макроскопического, мезоскопического, микроскопического и атомного. Конкретная шкала масштабных уровней устанавливается для различных классов материалов в соответствии с реализующимися механизмами деформирования (течения) и выполнением требования «представительности» объема соответствующего масштабного уровня. В МДТТ и, в частности, в теории пластичности в последние 10–20 лет широко используется другое важное понятие «структурные уровни (деформации)», основанное на выделении структурных дефектов материала, имеющих различную природу и происхождение, связанное с эволюцией дефектных структур по различным механизмам деформирования и характерных параметров (внутренних переменных), описывающих эволюцию и взаимодействие дефектов различных структурных уровней. Следует отметить, что процессы необратимого деформирования реализуются за счет одновременной или последовательной активизации механизмов различных структурных уровней. Масштаб структурных уровней определяется характерными размерами структурных неоднородностей. При формулировке ОС и ЭУ на различных масштабных уровнях каждому из них на основе тщательного физического анализа ставятся в соответствие определенные структурные уровни деформации и механизмы (моды) деформации; при этом один и тот же структурный уровень деформации может быть одновременно присущ нескольким масштабным уровням.

44

Возвращаясь к проблеме замыкания, следует отметить два наиболее употребительных подхода к ее решению. В первом – феноменологическом

– параметры, характеризующие структуру на более низких масштабных уровнях, определяются функциональными уравнениями через параметры рассматриваемого уровня (например, как в модели турбулентности Рейнольдса) с последующей экспериментальной проверкой этих уравнений. Второй подход основан на построении иерархической совокупности моделей нескольких масштабных уровней и установлении связей между однотипными характеристиками процесса деформирования соседних уровней. Следует отметить, что в этом случае полностью избежать феноменологических соотношений, конечно, не удается, однако они записываются для самого низкого масштабного уровня в принятой иерархической совокупности. Строго говоря, необходимы математические исследования «затухания» ошибок, внесенных при применении подобных феноменологических соотношений, при переходе на более высокие масштабные уровни.

В любом случае для замкнутой модели материала требуются уравнения, связывающие внутренние «явные» переменные, непосредственно входящие в ОС рассматриваемого масштабного уровня, с параметрами воздействия и внутренними скрытыми переменными. Общий вид таких замыкающих уравнений (ЗУ) мало отличается от ЭУ (19)–(20), однако они существенно различаются своим физическим «наполнением», подходами к их установлению и ролью в совокупности уравнений, модели материала, в связи с чем эти ЗУ выделяются в отдельную группу. Аналогично соотношениям (17)–(20) ЗУ могут быть записаны в одном из двух видов:

Таким образом, в качестве полной системы уравнений, описывающих поведение материала, будет рассматриваться совокупность (называе-

мая конститутивной моделью) ОС (17) (или (18)), ЭУ (19)(или (20)) и ЗУ

(21) (или (22)). При этом в некоторых теориях неупругого деформирования могут отсутствовать ЭУ (в принятом здесь смысле), ЭУ и ЗУ могут входить неявным образом в ОС. Правые части всех групп соотношений в качестве аргументов могут содержать части параметров Pα , Jeγ , Jiδ , а в не-

которых случаях в них может полностью отсутствовать тот или иной тип параметров (чаще всего – Jiδ ).

Вообще говоря, правые части в соотношениях (17)–(22) могут представлять собой достаточно сложные операторы, и при такой трактовке можно ввести классификацию конститутивных моделей по типу оператора (тензорно-алгебраические, дифференциальные, интегральные, интегродифференциальные по временной и пространственным переменным). Од-

45

нако в подавляющем большинстве случаев при использовании внутренних переменных соотношения конститутивной модели удается записать в виде тензорно-алгебраических уравнений, т.е. в виде тензорзначных функций тензорзначных аргументов, или в виде простейших (например, дифференциальных) операторов.

Вопрос выбора типа ОС, ЭУ и ЗУ – в терминах мер напряженного состояния и других параметров («интегральные» соотношения) или мер скоростей их изменения («дифференциальные» соотношения, соотношения скоростного типа) – в каждом конкретном случае решается исследователем. При этом учитываются соображения физического характера, сложности записи соотношений, ясности интерпретации результатов и т.д.; понятно, что в силу отсутствия четко определенных критериев подобный выбор во многом субъективен. Следует отметить, что общая система соотношений модели материала может содержать уравнения разных типов как по группам соотношений, так и внутри каждой из трех групп.

Опыт работы авторов в области построения моделей материалов свидетельствует о предпочтительности использования соотношений скоростного (дифференциального) типа. Вероятно, это связано с большей наглядностью и физической «прозрачностью» установления формы уравнений для скоростей изменения тех или иных параметров «здесь и сейчас» по сравнению с «интегральными» соотношениями, требующими «запоминания» предыстории воздействий. Следует сказать, что большинство известных авторам моделей материалов (особенно в теории пластичности) принадлежит именно скоростному типу. Авторы не исключают соотношения «интегрального» типа из рассмотрения, однако в рамках рассматриваемого в данном разделе подхода будем оперировать соотношениями скоростного типа.

Таким образом, ОС с внутренними переменными можно представить в следующем виде:

Здесь f( ) — тензорзначная (второго ранга) функция параметров Jβ ,Pγ и

их производных (обычных или независящих от выбора системы отсчета) по времени в момент времени t; в общем случае область определения указанных параметров (по пространственной переменной) — все исследуемое тело B.

Для краткости записи в дальнейшем объединим ЭУ и ЗУ в одну группу соотношений (например, алгоритмически) и в дальнейшем будем называть эти соотношения эволюционными или кинетическими. Принимая введенную гипотезу в качестве постулата, в дальнейшем при построении аксиоматики можно оперировать соотношением (23), дополненным эволюционными уравнениями для внутренних переменных Jβ вида

При этом fβ — тензорзначные функции соответствующего ранга, аргу-

менты которой определяются в исследуемый момент времени t.

Введенная гипотеза согласуется с принципом детерминизма; отсутствуют противопоказания для ее совместного использования с аксиомами 2 и 3. В частности, при использовании принципа локальности в качестве аргументов в правых частях (23), (24) можно использовать значения параметров Jβ ,Pγ (и, возможно, градиентов части из них) и их производных

в точке R0 в момент t. Использование принципа материальной индифферентности позволяет конкретизировать вид соотношений (23)–(24); в частности, может привести к необходимости замены материальных производных по времени теми или иными независящими от выбора системы отсчета производными.

Предлагаемый общий вид ОС (23)–(24) представляется более удобным для последующего анализа и приложений, чем запись ОС в операторной форме (9). В частности, для соотношений (23)–(24) в полной мере могут быть использованы хорошо разработанные в тензорном анализе теория тензорных функций тензорных аргументов, теория инвариантов и другие разделы тензорного исчисления и анализа.

Вопросы для самопроверки

1.Сформулируйте основную гипотезу, позволяющую перейти от операторной формы ОС к конститутивной модели с простыми операторами.

2.Приведите определение внутренних переменных и конкретные примеры, поясняющие их смысл.

3.В чем отличие внутренних неявных переменных от внутренних явных переменных?

4.В чем состоят преимущества и недостатки конститутивных моделей, основанных на введении внутренних переменных?

5.Запишите все соотношения конститутивной модели.

6.В чем состоит проблема замыкания конститутивных соотношений и какие подходы к её решению Вам известны?

7.Поясните значение и физический смысл эволюционных и замыкающих уравнений.

47

5. Примеры применения принципа индифферентности

Как уже было отмечено выше, приведенные аксиомы играют важную роль в установлении конкретного вида ОС, особенно для «отбраковки» некорректных физических уравнений. Особое место в этой связи занимает принцип независимости от выбора системы отсчета [7], конструктивные примеры использования которого рассматриваются в данном пункте.

Пример 1.

Для упрощения рассуждений и преобразований используем ОС, описывающие реакцию материала (напряженное состояние) только на механическое движение (изменение конфигурации). В рамках модели простого материала в этом случае можно воспользоваться частным видом ОС, следующим из (16):

σ(r,t) Fˆ [ rt ].

Как известно из кинематики, градиент места может быть представлен скалярным произведением левой меры искажения и ортогонального тензора ротации. При рассмотрении движения с позиций двух наблюдателей история изменения левого тензора искажений остается одинаковой, а история поворотов может как угодно различаться (она зависит от вращения одной подвижной системы относительно другой, которое может быть каким угодно). Если история тензора ротации действительно является существенным аргументом, то отклик материала может существенно меняться при заменах систем отсчета. Допустимо ли это? С физической точки зрения это, конечно, представляется абсурдным.

Докажем, что тензорзначная функция σ(r,t) для простых материалов

определяется только предысторией левого тензора искажений Ut, предыстория поворотов не оказывает влияния на σ(r,t) , в ОC могут вхо-

ортогональный тензор, сопровождающий деформацию. Тогда из последнего соотношения следует:

Fˆ[( U R O)t ] OT (t) Fˆ ( rt ) O(t) .

48

Вышеприведенные соотношения выполняются O O. В частности, можно положить O(t) = RT(t) t. Иначе говоря, в качестве системы 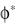используется подвижная система, поворот которой описывается тензором ротации главных осей правой меры искажения V к главным осям левой меры искажения U. В терминах наложенного жесткого движения это означает, что поворот описывается тензором RT. В этой подвижной системе

σ (r , t) Fˆ(Ut ) .

Возвращаясь к исходной системе отсчета , получаем

σ(r, t) RT (t) σ (r , t) R(t) RT (t) Fˆ (Ut ) R(t).

Последнее соотношение называется приведенной формой ОС; в соответствии с ним история прошлых поворотов не сказывается на определяющем отображении, повороты могут входить в ОС лишь своими значениями в текущий момент времени. От введенной подвижной системы 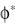можно перейти и к любой другой 1, поворот которой описывается тензорзначной функцией, t O1(t) O . Аргумент в правой части предыдущего соотношения при этом не изменится, т.к. U является инвариантной по отношению к наложенному жесткому движению мерой деформации. Следовательно, в силу индифферентности тензора напряжений Коши для любой

что и доказывает требуемое утверждение.

Приведенная форма ОС позволяет существенно упростить построение конкретных физических уравнений. Действительно, в этом случае следует установить функциональную зависимость σ от предысторий только «чистого» деформирования Ut (при Rt = E), откуда с использованием последнего соотношения можно перейти к ОС с любой предысторией деформации. Следует отметить, что существуют и другие приведенные формы ОС.

Подчеркнем, что история «чистой» деформации Ut представляет собой не только историю изменения растяжений-сжатий вдоль фиксированных материальных волокон, совпадающих с главными осями меры U для любого момента времени. В историю Ut входит и история поворотов главных векторов меры U относительно материальных волокон. В связи с вышесказанным не следует воспринимать термин «чистая» деформация буквально, иначе необходимо было бы рассматривать лишь узкий класс процессов деформирования (растяжений-сжатий вдоль трех взаимно перпендикулярных фиксированных материальных волокон).

49

В предположении отсутствия памяти и зависимости от времени (склерономности) материала приходим к модели материала, называемого упругим. В соответствии с полученным результатом приведенная форма ОС такого материала имеет вид

ˆ

σ(r) f (U) ,

где ˆ – тензорзначная (второго ранга) функция. f (·)

Пример 2.

Одной из сложнейших задач МДТТ является проблема построения ОС для случая геометрически нелинейных проблем (больших градиентов перемещений). В настоящее время ее решение часто осуществляется обобщением известных «геометрически линейных» ОС. В качестве примера рассмотрим обобщение ОС Максвелла на случай больших градиентов перемещений. Определяющие соотношения Максвелла имеют вид

напряжений Коши в левой части уравнения приводит к нарушению требования индифферентности ОС (25). Действительно, в соответствии с требованием индифферентности (аксиомой N3) вид уравнения не должен меняться при замене системы отсчета (или наложении жесткого движения). Тогда из (25) должно следовать

2 D .

Последнее соотношение, как нетрудно видеть, не совпадает по виду с ОС

·

(25). Причина кроется в неиндифферентности производной σ (несмотря на индифферентность σ ).

Выход из данной ситуации в большинстве работ по геометрически

·

нелинейным ОС заключается в замене материальной производной σ на коротационную или конвективную производную σr . В этом случае определяющее соотношение (25) имеет вид

50

При малых квазижестких поворотах (и малых скоростях этих поворотов) соотношение (26) сводится к (25). Возникающая при таком подходе к обобщению ОС неединственность выбора независимых от системы отсчета мер скоростей напряжений, деформаций и других параметров разрешается с привлечением дополнительных гипотез и физического анализа.

Следует отметить сложность и важность решения данного вопроса, поскольку физически необоснованный выбор объективных производных может привести к качественно неверным результатам, зачастую трудно выявляемым на предварительной стадии оценки модели. При этом самым сложным является вопрос определения «движения без жесткого вращения» сплошной среды. Данный вопрос в исследованиях по нелинейной механике часто подменяется проблемой независимости ОС от выбора системы отсчета. Конечно, последнее требование должно быть выполнено; как показано выше, осуществить его выполнение достаточно просто. Однако это не снимает вопроса о выборе меры поворота при обобщениях геометрически линейных соотношений на случай больших градиентов перемещений. Действительно, в общем случае движения деформируемой среды невозможно выделить тройку некомпланарных материальных волокон, сохраняющих свою взаимную ориентацию в течение всего исследуемого процесса движения. (При наличии такой тройки меру поворота тройки единичных векторов вдоль выбранных материальных волокон можно с полным основанием считать мерой жесткого поворота). При произвольном движении деформируемой среды любая выбранная тройка волокон испытывает изменение углов между ними.

В связи с этим в нелинейной механике часто применяется понятие квазитвердого движения, вводимого для принятого представления дви-

жения среды совокупностью квазитвердого и деформационного дви-

жений. Именно мера последнего вводится в определяющее соотношение как эквивалент меры деформаций в геометрически линейном ОС. Ортогональная тензорзначная функция, характеризующая поворот в квазитвердом движении, используется затем при определении коротационных производных. Заметим, что данный подход тоже не может претендовать на единственность. Однако в любом случае введение мер квазитвердого движения, способа обобщения геометрически линейного ОС на случай больших градиентов перемещением, анализ принимаемых при этом гипотез должны предшествовать экспериментальным исследованиям и лежать в основе программы экспериментов, учитываться при интерпретации и обработке опытных данных.