Свойства векторного произведения:

1. Векторное произведение антикоммутативно, т.е. [а, b] = - [b, а];

2. [а+ b, с] = [а, с] + [b, с];

3. ;

4. [а, b] = 0 тогда и только тогда, когда векторы а и b коллинеарны;

5. (Геометрический смысл векторного произведения). Длина векторного произведения векторов а и b равна площади параллелограмма, построенного на этих векторах.

Док-во: 1. При изменении порядка сомножителей плоскость, в которой лежат сомножители, остается прежней, поэтому остается прежней прямая, перпендикулярная этой плоскости, однако кратчайший поворот от первого сомножителя до второго теперь виден с другой стороны, следовательно, произведение меняет знак;

1. Второе свойство будет доказано позже, после изучения свойств смешанного произведения;

2. Если , то вектор [а, b] растягивается (при ) или сжимается (при ) в раз; если , то [а, b] еще меняет и направление;

3. [а, b] = 0, как уже говорилось, тогда и только тогда, когда либо по крайней мере один из этих векторов – нулевой, либо , либо ; во всех этих случаях векторы коллинеарны;

4. Если на векторах а и b построить параллелограмм и рассматривать а как основание, то высота параллелограмма равна 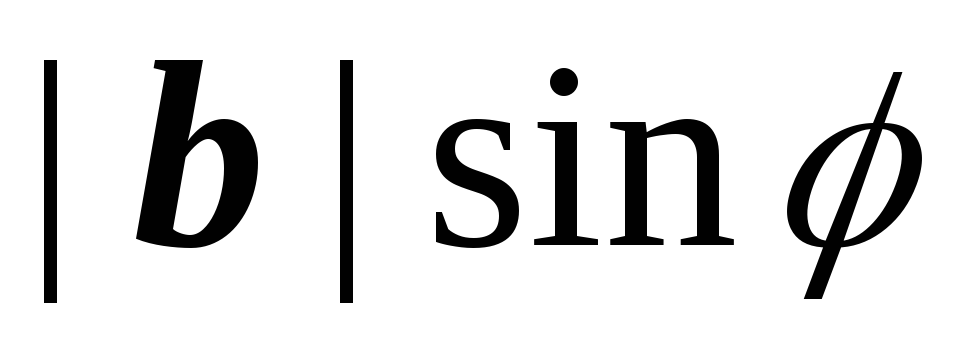. Следствием из пятого свойства является то, что площадь треугольника, построенного на векторах а и b, равна половине длины их векторного произведения.

Упорядоченная тройка некомпланарных векторов a, b, c называется правой, если при приведении этих векторов к общему началу кратчайший поворот от a к b виден из конца вектора c против часовой стрелки (если кратчайший поворот от a к b совершается по часовой стрелке, то тройка векторов a, b, c называется левой).

Заметим, что если тройка a, b, c – правая (левая), то правыми (левыми) являются тройки b, c, a и c, a, b, т.е. ориентация не меняется при циклической перестановке векторов. В тоже время перестановка двух векторов меняет ориентацию: если тройка a, b, c – правая (левая), то тройка b, a, c (и, как следствие, тройки a, c, b и c, b, a) – левая (правая).

Ортонормированный базис в пространстве будем задавать правой тройкой ортов i, j, k. Произвольный вектор пространства a теперь может быть представлен в виде . На рисунке справа х = ОА₂, у = ОА₃, z = ОА₄, все три координаты положительны. Если х, у, z – координаты вектора а в ортонормированном базисе, то (док-во: |a|² = ОА² = ОА₁² + A₁А² (так как тр-к OAA₁ – прямоугольный) = (ОА₂² + A₂А₁²) + A₁А² = ОА₂² + ОА₃² + ОА₄²).

Определение векторного произведения векторов. Векторным произведением векторов а и b называется вектор с, длина и направление которого определяются следующими условиями:

1. (или ;

2 ;

3. a, b, с - правая тройка (если векторы а и b не коллинеарны).

Обозначения: [а, b], .

Заметим, что три условия в определении векторного определения однозначно определяют результат. Первое условие определяет длину вектора с ( так как ), второе – перпендикулярность произведения плоскости, содержащей сомножители, третье определяет нужное направление на прямой, перпендикулярной этой плоскости. Оговорка по поводу неколлинеарности сомножителей в третьем условии не сужает определение: если а и b коллинеарны, то либо по крайней мере один из этих векторов – нулевой, либо , либо ; во всех этих случаях векторное произведение дает нуль-вектор.