Червячный редуктор

Червячная передача передает вращательное движение между валами, геометрические оси которых перекрещиваются чаще всего под углом …. Она позволяет осуществить большие передаточные отношения от 5 до 1500 при помощи одной пары. Червячная передача построена на базе реечного эвольвентного зацепления. Профилем винтовой нарезки червяка служит исходный контур нормального эвольвентного зацепления, для которого .

Червячные передачи работают плавно и бесшумно, при малых боковых зазорах в зацеплении.

К недостаткам червячных передач по сравнению с зубчатыми относятся низкий КПД (из-за больших потерь на трение в зацеплении витков червяка с зубьями червячного колеса) и необходимость по этой причине выполнять червячные колеса или их зубчатые венцы из дорогостоящих антифрикционных материалов (например, из бронзы).

Наиболее распространены червячные передачи, в которых ведущим кинематическим звеном является червяк.

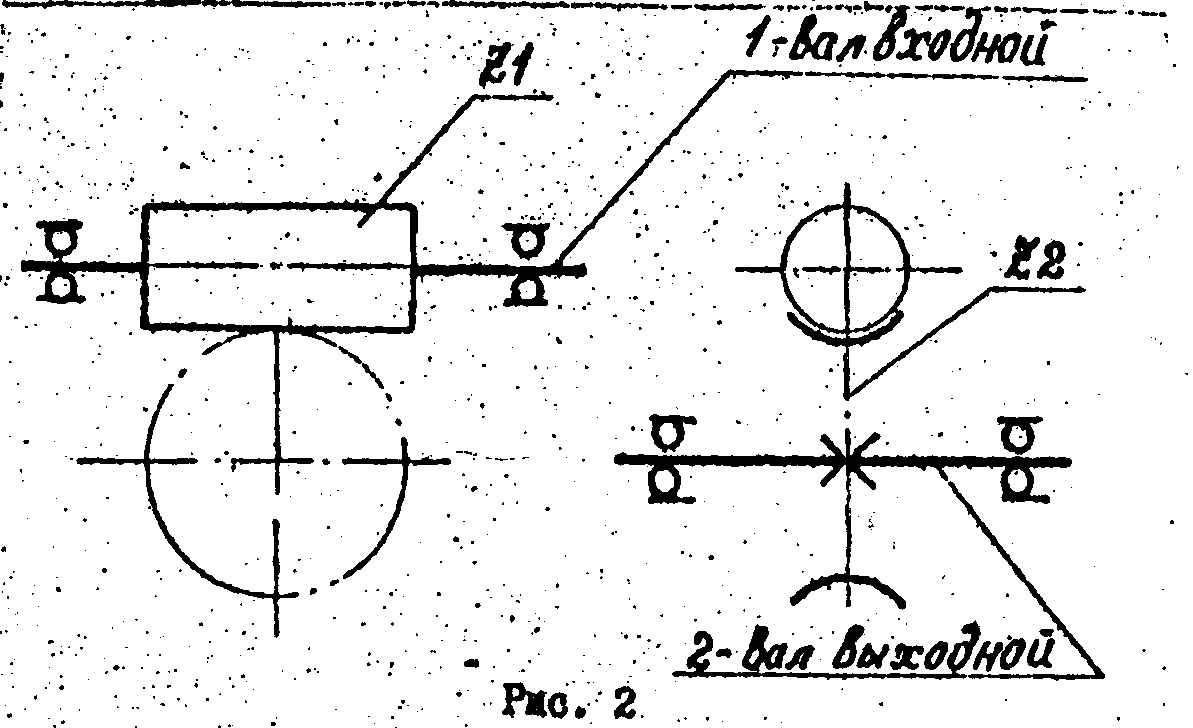
Кинематическая схема исследуемого одноступенчатого червячного редуктора с ведущим червяком представлена на рис. 2. Передаточное отношение такого редуктора равно:

(14)

где n₁— частота вращения червяка, об/мин;n₂— частота вращения червячного колеса об/мин;Z₁— число заходов червяка;Z₂— число зубьев червячного колеса.

Зависимость между моментов M₁, действующим на червяк, и моментом на червячном колесеимеет вид

(15)

где — коэффициент полезного действия червячной передачи при ведущем червяке, определяемый по формуле

(16)

где — угол подъема линии витка червяка, ;q— коэффициент диаметра червяка, зависящий от числа заходов и угла;— угол трения.

Наиболее часто угол оказывается в пределах отдо.

здесь f— коэффициент трения между поверхностями червяка и червячного колеса в точке их соприкосновения;— угол профиля винтовой нарезки червяка.

Для приборных червячных передач, работающих с ведущим червяком, с учетом влияния нагрузки КПД формула (16) имеет вид

(17)

где ,;F₂— окружное усилие на червячном колесе, Н,;d₂— диаметр начальной окружности червячного колеса,.

Общий КПД исследуемого редуктора определяется по формуле

(18)

Для данного редуктора применяется пара сталь-бронза, для которого коэффициент трения , червях двухзаходный, число зубьев червячного колеса, модуль передачимм, параметр червяка,,,.

Задавшись несколькими значениями (согласно варианту работы), можно определить КПД и построить теоретическую зависимость.

Планетарный редуктор

Планетарный редуктор представляет собой зубчато-рычажное устройство, в котором геометрические оси одного или нескольких колес перемещаются в пространстве. Планетарные передачи обладают рядом достоинств. Переход от обычных передач к планетарным обеспечивает снижение веса в 1,5-5 раз, приводит к уменьшению габаритов (при тех же передаточных отношениях). В зависимости от схемы планетарные передачи могут осуществлять передаточные отношения от 3 до 1000 при КПД от 0,98 до 0,01 соответственно. Ведущий и выходной валы расположены соосно.

Планетарный механизм состоит из трех частей:

1. солнечного колеса, геометрическая ось которого не изменяет своего положения в пространстве;

2. сателлита, геометрическая ось которого перемещается по окружности;

3. водила, поддерживающего ось сателлита при его вращении.

При работе планетарной передачи сателлит обегает вокруг солнечного колеса подобно тому, как планеты движутся вокруг солнца. Поэтому передача и называется планетарной.

Планетарные передачи могут быть использованы для сложения различных движений. В этом случае они называются дифференциалами.

Меньшие размеры и вес планетарных передач по сравнению с соответствующими зубчатыми передачами с неподвижными осями объясняются тем, что применение двух или трех сателлитов позволяет уменьшить нагрузку на зубья колес и использовать колеса с меньшими модулями и диаметрами. Передачи отличаются также высокой надежностью и малыми потерями на трение.

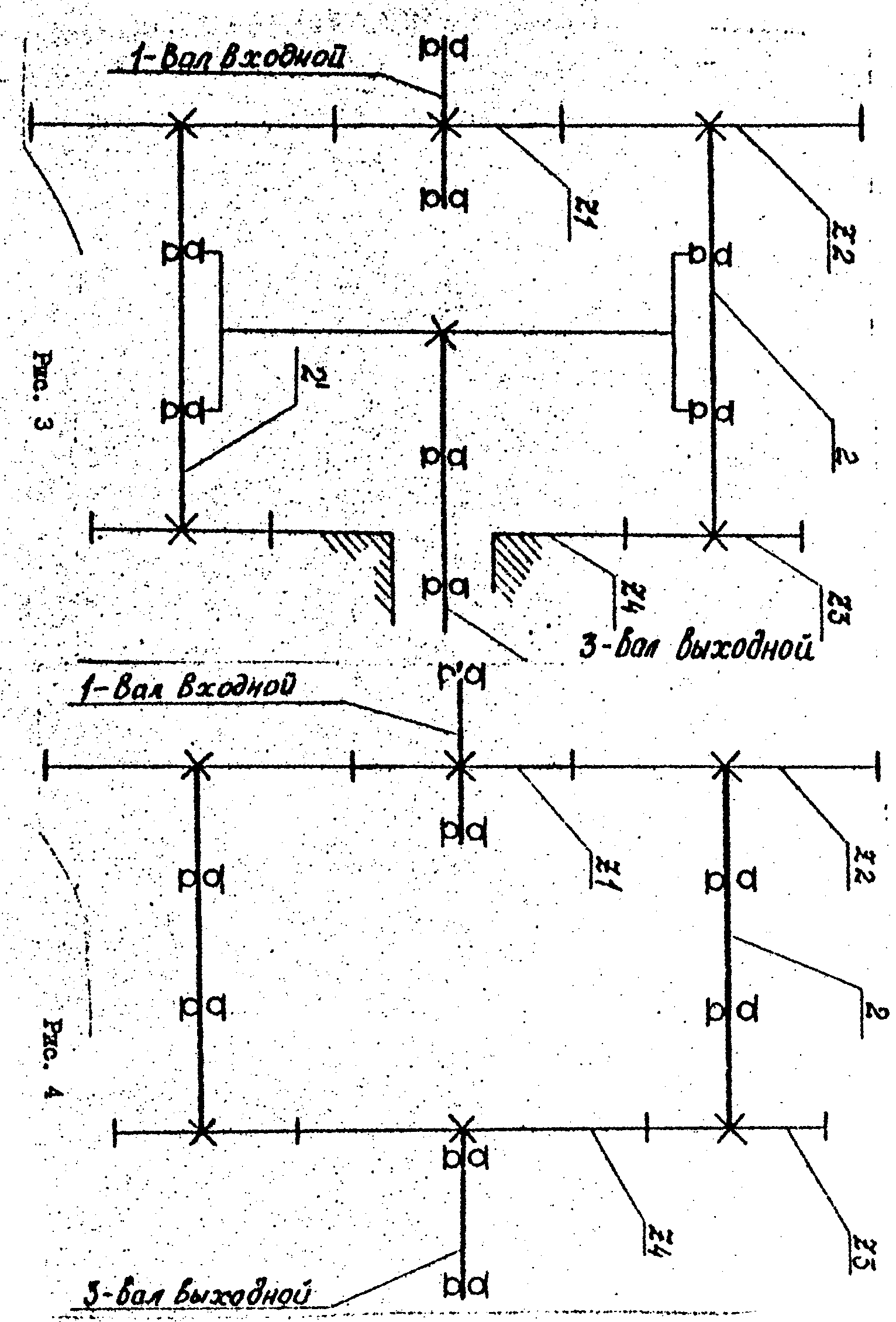
На рис. 3 показана кинематическая схема планетарного редуктора, который использован в лабораторной установке. Он состоит из двух спаренных планетарных передач. Солнечные колеса имеют числа зубьев и, причем колесоZ₆неподвижно. Числа зубьев сателлитовZ₂иZ₃. Модуль зацепления мм. Сателлиты жестко закреплены на общей оси 2. Их угловые скорости одинаковы. Водило (выходной вал) 3 поддерживает перемещающуюся по окружности ось сателлитов. Ведущим является солнечное колесоZ₁, ведомым кинематическим звеном редуктора – водило.

Передаточное отношение планетарного механизма определяется методом обращенного движения (остановки водила). Условно всем звеньям механизма сообщается дополнительное движение с угловой скоростью водила , но в сторону, противоположную вращению последнего. Кинематическая схема обращенного механизма представлена на рис. 4.

Для каждой из двух планетарных передач можно написать выражение основной формулы планетарной передачи

;

где i_n1иi_n2— передаточные отношения планетарных передач при неподвижном водиле;и— угловые скорости солнечных колесZ₁иZ₄();— угловая скорость водила. Угловые скорости берутся с учетом направления вращения.

Учитывая, что , получим .

Тогда передаточное отношение планетарного редуктора равно

(19)

Если водило остается неподвижным, то планетарный редуктор становится обычной зубчатой передачей с неподвижными осями. Его передаточное отношение равно

(20)

Составим уравнение внешних моментов, действующих на планетарный редуктор

(21)

где M₁— момент солнечного колесаZ₁;M₄— реактивный момент солнечного колесаZ₄;M_в— момент водила.

Коэффициент полезного действия обращенного механизма равен

откуда

(22).

Моменты M₁иM₄имеют противоположные направления. Заменим в равенстве (22) его выражением из равенства (21)

Коэффициент полезного действия планетарного редуктора равен:

(23)

При подсчете по формуле (23) передаточные отношения планетарного редуктора и обращенного механизма определяются по формулам (19) и (20). Коэффициент полезного действия обращенного механизма принимается равным

(24)

где и— КПД первой и второй ступеней обращенного механизма, определяемый по формулам (11) и (12) для КПД эвольвентного зубчатого зацепления.

Окружные усилия в зацепления можно определить из условия равновесия сил и моментов относительно вала сателлитов 2 (рис. 5):

(25)

(26)

где r₂— радиус сателлитаZ₂;r₃— радиус сателлитаZ₃;F₁₂— окружное усилие в зацеплении колесZ₁иZ₂;F₃₄— окружное усилие в зацеплении колесZ₃иZ₄;

F_в— окружное усилие на водиле.

(27)

Решая совместно уравнения (25) и (26) с учетом выражения (27), находим

(28)

(29)

Задаваясь несколькими значениями момента нагрузки, т.е. момента M_в, определим для каждого значенияF₁₂иF₃₄по формулам (28) и (29). Затем находимипо формулам (11) и (12). Общий КПД планетарного редуктора определяем из (23) и (6):

(30)

где — КПД одной пары подшипников;;— число пар подшипников.

По найденным значениям можно построить теоретическую зависимость

.