
385
.pdfМинистерство образования Российской Федерации Омский государственный университет
Исследование симметричного и асимметричного dc-сквидов
Лабораторный практикум (для студентов физического факультета)
Специальность 010400 «Физика»
Издание |
Омск |
ОмГУ |
2004 |
УДК 538. 945 И88
Рекомендован к изданию учебно-методическим советом ОмГУ. Протокол № 1 от 28 апреля 2004 г.
И88 Исследование симметричного и асимметричного dc-сквидов: Лабораторный практикум (для студентов физи- ческого факультета) / Сост.: Н.В. Блинов, О.Л. Курнявко, Д.C. Пашкевич, И.В. Широков, К.Н. Югай. – Омск: Омск. гос.
ун-т, 2004. – 28 с.
Практикум включает две лабораторные работы. Материал соот- ветствует Государственному образовательному стандарту по специ- альности 010400 «Физика».
Может быть использован студентами других специальностей.
УДК 538. 945
© Омский госуниверситет, 2004
2
ЛАБОРАТОРНАЯ РАБОТА № 1 Исследование симметричного dc-сквида
Сквиды – это сверхпроводящие сенсоры, позволяющие изме- рять чрезвычайно слабые магнитные поля. Само слово сквид – это русское произношение английской аббревиатуры SQUID – Superconducting Quantum Interference Device (сверхпроводящее квантовое интерференционное устройство). С помощью сквидов можно соз- дать магнитометры с чувствительностью порядка 10–11 Гс, вольтмет- ры с чувствительностью порядка 10–15 В и другие приборы с очень высокой чувствительностью. Открытие в 1986 году Беднорзом и Мюллером высокотемпературных сверхпроводников – металлоок- сидных керамик – сделало приборы на основе сквидов доступными для широкого использования.
Различают два вида сквидов: сквид на постоянном токе – dc-сквид (двухконтактный сквид) и высокочастотный – rf-сквид (од- ноконтактный). Ниже рассматриваются свойства dc-сквида. Причем используется простейшая модель dc-сквида – симметричная модель, в которой предполагается полное равенство плеч сквида.
Цель лабораторной работы – исследовать симметричный dc-сквид с помощью численного решения системы уравнений для dc-сквида; для ряда конкретных параметров сквида найти важней- шие характеристики сквида: вольтамперную и вольтпотоковую ха- рактеристику, его чувствительность.
Уравнение симметричного dc-сквида
Dc-сквид состоит из двух джозефсоновских переходов, вклю- ченных в сверхпроводящее кольцо с индуктивностью L. Это кольцо называют контуром квантования. При наведении на сквид внешнего
потока магнитного поля Φe возникающее на сквиде напряжение V является периодической функцией Φe при постоянном токе смеще- ния I.
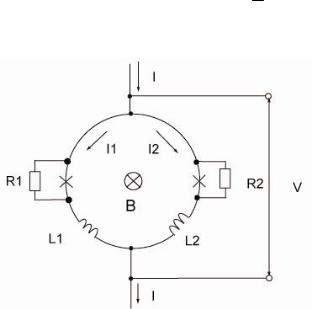
Схема dc-сквида изображена на рис. 1. В симметричном dc- сквиде критические токи левого и правого переходов, отмеченных на рис. 1 крестиками, равны Ic1 = Ic2 ≡ Ic , равны также сопротивле-
ния R1 = R2 ≡ R и индуктивности плеч L1 = L2 = L2 , где L – полная индуктивность кольца.
Рис. 1. Схема dc-сквида
Уравнение dc-сквида основывается на двух соотношениях
Джозефсона: |
|
|
|
Is = Ic sin ϕ, |
(1) |
||
h |
∂ϕ |
= 2eV , |
(2) |
|
∂t |
|
|
где Is – сверхпроводящий ток через джозефсоновский переход; ϕ –
разность фаз волновых функций сверхпроводящего конденсата на переходе; V – напряжение на переходе. Уравнение (1) определяет стационарный эффект Джозефсона, а уравнение (2) нестационарный эффект.
3 |
4 |
Полный ток смещения в сквиде |
|
I = I1( t ) + I2( t ) = const. |
(3) |
Несмотря на то, что I = const, токи I1 и I2 являются в общем случае функциями времени из-за возникновения индуцированного внешним переменным магнитным полем кругового тока в кольце. Ток I1, а также ток I2 имеет две компоненты: сверхпроводящую и нормальную:
I ( t ) = I |
c |
sinϕ ( t ) + |
V1( t ) |
, |
|
(4) |
||||||||||||
|
|
|
||||||||||||||||
1 |
|
|
|
|
|
|
|
1 |
|
|
|
R1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
I2( t ) = Ic sinϕ2 |
( t ) + |
V2( t ) |
. |
|
(5) |
|||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|||
Разность фаз ϕ1 и ϕ2 согласно (2) определяются уравнениями: |
|
|||||||||||||||||
|
¶ϕ1 |
= |
2e |
V ( t ), |
|
(6) |
||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
¶t |
|
|
|
|
|
h |
1 |
|
|
|
|
|
|
|
|||
|
¶ϕ2 |
|
= |
|
2e |
V ( t ) . |
|
(7) |
||||||||||
|
|
¶t |
|
|
|
|
||||||||||||
|
|
|
|
|
|
h |
2 |
|
|
|
|
|
|
|
||||
Напряжение на сквиде V определяется следующим образом: |
|
|||||||||||||||||
V( t ) = V1( t ) + L1 |
dI1( t ) |
= V2( t ) + L2 |
dI2( t ) |
. |
(8) |
|||||||||||||
|
|
dt |
|
|
dt |
|||||||||||||
Уравнения (3)–(8) в принципе описывают работу dc-сквида, поскольку влияние внешнего магнитного поля учитывается зависи- мостью I1 и I2 от времени, что в свою очередь позволяет найти раз- ность потенциалов на сквиде (8). Однако удобнее явно ввести поток внешнего магнитного поля в уравнение dc-сквида. Это можно сде- лать следующим образом: введем круговой ток в контуре
J( t ) = |
I2( t ) - I1( t ) |
. |
(9) |
|
|||
2 |
|
|
|
С помощью выражения для полного потока Φ , сцепленного с |
|||
контуром |
|
||
F( t ) = Fe( t ) - LJ( t ) , |
(10) |
||
можно записать круговой ток J в виде |
|
|||
J = Fe( t ) - |
F( t ) . |
(10’) |
||
|
|
L |
L |
|
Полный поток Φ связан с разностью ϕ2 -ϕ1 |
соотношением |
|||
ϕ |
2 |
-ϕ = 2π F( t ) , |
(11) |
|
|
1 |
F0 |
|
|
|
|
|
|
|
где F0 = πeh – квант потока. Покажем справедливость соотношения
(11).
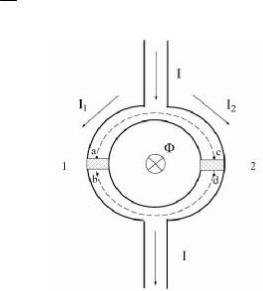
Рис. 2. К выводу соотношения (11): штриховыми линиями изображены контуры, по которым проводят интегрирование
Проведем внутри кольца контуры ac и db, соединяющие пары точек, расположенных вблизи переходов (рис. 2). Обобщенный им-
пульс куперовской пары имеет вид: |
|
r |
(12) |
hÑθ = 2mvs + 2eA, |
где θ – фаза волновой функции сверхпроводящего конденсата; vs –
скорость куперовской пары. Полагая, что контуры ac и db располо- жены на расстоянии от края кольца, превышающем лондоновскую
5 |
6 |

глубину проникновения магнитного поля |
λ , |
и интегрируя (12) по |
|||
этим контурам, получим |
|
|
|
|
|
θa -θc +θd -θb = |
2e |
æ a r r |
d |
r rö |
|
ç |
|
÷ |
(13) |
||
|
|
||||
h |
çò Adl |
+ ò Adl ÷. |
|||
|
è c |
b |
ø |
|
|
Вводя обозначение разности фаз на |
левом ϕ1 и правом ϕ2 |
переходах |
|||
θb -θa = ϕ1, |
θd -θc = ϕ2 |
(14) |
|||
и учитывая, что расстояние между точками a и b, а также c и d малы
по сравнению с длинами контуров ca и bd, получаем |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2e |
|
|
|
|
|
|
r |
|
r |
F |
|
|
|
|
|
||||||
|
ϕ2 -ϕ1 = |
|
ò |
Adl = 2π |
, |
|
|
|
|
|||||||||||||||||||||
h |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
abcda |
|
|
|
|
F0 |
|
|
|
|
||||||||||||
поскольку по теореме Стокса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
ò Adl = òrot AdS = òH dS = F, |
|
||||||||||||||||||||||||||||
|
abcda |
|
|
|
S |
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|||||||||
где S – площадь контура квантования. |
|
|
|
|
|
|
||||||||||||||||||||||||
С учетом (11) выражение для кругового тока запишем в виде |
||||||||||||||||||||||||||||||
|
|
J( t ) |
= |
|
2 |
|
Fe |
- |
|
ϕ2( t ) -ϕ1( t ) |
, |
|
(15) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
Ic |
|
|
|
|
β F0 |
|
|
|
|
πβ |
|
|
|
|
|
|
||||||||||||
где введем параметр β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
β = |
|
2Ic L |
. |
|
|
|
|
|
|
|
(16) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F0 |
|
|
|
|
|
|
|
|
|
|
||||||
В выражении (9), подставляя вместо I1 или I2 , соответствующее вы- |
||||||||||||||||||||||||||||||
ражение из (3), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
J( t ) = |
|
I - 2I1( t ) |
|
= |
- I + 2I2( t ) |
, |
|
(17) |
|||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||
откуда имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dJ( t ) |
= - |
dI1( t ) |
, |
|
dJ( t ) |
= |
dI2( t ) |
. |
(18) |
||||||||||||||||||||
|
dt |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
dt |
dt |
|
|
|
|
|||||||||
Учитывая (18), можно записать выражение для разности потенциа- лов на сквиде V(t) в виде
V( t ) = V ( t ) - |
L |
|
dJ( t ) |
|
= V ( t ) + |
L |
|
dJ( t ) |
. |
(19) |
|
|
|
|
|||||||
1 |
2 dt |
2 |
2 dt |
|
||||||
|
|
|
||||||||
Отсюда с учетом (6) и (7) получаем |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
V +V |
|
|
|
|
|
|
|
h |
æ dϕ ( t ) |
|
dϕ |
2 |
( t ) ö |
|
||||||||||||||
V( t ) = |
|
|
1 |
|
|
2 |
|
= |
|
|
ç |
|
|
|
1 |
|
|
+ |
|
|
|
÷. |
(20) |
|||||||||
|
|
|
2 |
|
|
|
|
|
|
|
dt |
dt |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4e è |
|
|
ø |
|
||||||||||||
Подставляя в (6) и (7) соответствующие выражения для V1 и V2 из (4) |
||||||||||||||||||||||||||||||||
и (5), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dϕ1 |
|
|
= |
|
2eR |
|
|
|
(I ( t ) - I |
c |
sinϕ ( t )), |
|
|
(21) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
dt |
|
|
|
|
|
|
h |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dϕ2 |
|
|
|
= |
|
2eR |
|
|
|
|
(I2( t ) - Ic sinϕ2( t )). |
(22) |
|||||||||||||||||||
|
|
|
|
h |
|
|
|
|||||||||||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из соотношений (3) и (9) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
I |
|
= |
1 |
|
- J , |
I |
2 |
= |
1 |
+ J . |
|
|
|
|
(23) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
Подставляя (23) в (21) и (22), получаем |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
dϕ |
|
|
|
|
|
2eR |
æ |
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
||||||
|
1 |
= |
|
|
|
|
|
ç |
|
|
|
|
- J( t ) - I sinϕ ( t )÷, |
(24) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
dt |
|
|
|
|
|
|
h |
è 2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
ø |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
dϕ |
2 |
|
|
|
|
|
2eR |
æ |
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|||||
|
|
|
= |
|
|
|
|
|
ç |
|
|
|
+ J( t ) - I sinϕ ( t )÷. |
(25) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
dt |
|
|
|
|
|
|
h |
è 2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
ø |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Уравнения (15), (20), (24) и (25) составляют систему уравнений, опи- сывающих dc-сквид без учета шума. Для удобства вычислений пе- рейдем к безразмерным величинам. Введем обозначения:
h |
= |
h |
= |
F0 |
ºτ |
c |
, V = I |
R = |
h |
. |
|
|
|
|
|||||||
2eRIc |
|
2eVc |
2πVc |
c c |
|
2eτc |
||||
|
|
|
|
|||||||
С учетом этих обозначений образуем безразмерные величины:
|
|
t |
® t, |
|
|
I |
|
º i, |
J |
º iL , |
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
τc |
|
|
|
|
|
Ic |
|
|
|
Ic |
|
|||||||
|
|
V º v, |
|
|
L |
º l, |
|
Fe |
º φe . |
|
|||||||||
|
|
|
|
|
|
||||||||||||||
|
|
Vc |
|
|
|
|
|
|
Lc |
|
|
F0 |
|
||||||
Тогда система уравнений dc-сквида записывается в виде: |
|
||||||||||||||||||
|
|
dϕ1 |
= |
|
i |
- i |
L |
( t ) - sinϕ ( t ), |
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
dt |
2 |
|
|
|
|
1 |
|
||||||||||
|
dϕ2 |
|
= |
i |
|
+ iL( t ) - sinϕ2( t ), |
(26) |
||||||||||||
|
|
|
|||||||||||||||||
|
|
dt |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
7 |
8 |
|
1 |
æ dϕ ( t ) |
|
dϕ |
2 |
( t )ö |
|
|
2φ |
e |
|
ϕ |
|
-ϕ |
|||
v = |
|
ç |
1 |
|
+ |
|
|
÷ |
, i |
= |
|
- |
|
2 |
1 . |
||
|
|
|
|
|
|
|
|
||||||||||
|
2 |
è |
dt |
|
dt |
ø |
L |
|
β |
|
|
|
πβ |
||||
|
|
|
|
|
|
|
|||||||||||
В общем случае система уравнений (26) может быть решена только численно. Интегрируя (26), можно определить все важней- шие характеристики сквида, а также чувствительность, определяе-
мую выражением
æ |
¶V |
ö |
ç |
÷ |
|
S = ç |
|
÷ . |
è |
¶Fe øI |
|
Критический ток, вольтамперная, вольтпотоковая характеристики и чувствительность dc-сквида
Пусть Fe = 0 , тогда при токе смещения I, меньшем удвоенно-
го значения критического тока Ic, I < 2Ic, ток, протекающий через джозефсоновские переходы, будет являться сверхпроводящим
I = I1s( t ) + I2s ( t ) = Ic (sinϕ1 + sinϕ2 ) |
|
||||
или |
ϕ2 -ϕ1 |
|
ϕ1 + ϕ2 |
|
|
I = 2Ic cos( |
)sin( |
). |
(27) |
||
|
2 |
|
2 |
|
|
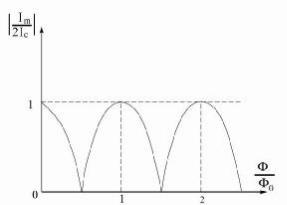
Рис. 3. Зависимость максимального сверхтока Im от полного потока в контуре Φ
Используя (11), запишем ток I в виде |
|
|||||||
I = 2I |
|
cos(π |
F |
)sin(π |
F |
+ ϕ ). |
(28) |
|
c |
|
|
||||||
|
|
|
F0 |
F0 |
|
|||
Отсюда можно видеть, что максимальный сверхпроводящий ток |
|
|||||||
|
|
Im = 2Ic cos(π |
|
F |
) |
(29) |
||
|
|
|
|
|||||
|
|
|
|
|
|
F0 |
|
|
является периодической функцией полного потока, захваченного контуром. Как видно из рис. 3, |Im| = 2Ic при F = nF0 , где n = 0,1,2,...,
т. е. при целом значении квантов захваченного потока. При числе квантов, равном полуцелому числу n+1/2, Im=0. Зависимость Im от
внешнего потока Fe |
будет также функцией от индуктивности кон- |
|||||||
тура или от параметра β . В соответствии с выражением (10) |
|
|||||||
æ |
|
π |
ö |
æ |
Fe |
|
ö |
|
ç |
|
÷ |
ç |
|
πβJ ÷ |
|
||
Im = 2Ic cosç |
|
|
(Fe - LJ )÷ |
= 2Ic cosçπ |
|
- |
÷ |
(30) |
|
|
F0 |
||||||
è F0 |
ø |
è |
|
2Ic ø |
|
|||
зависит от параметра β . Чем больше β , тем меньше разность D Im между значениями Im при Fe = 0 и его значением при Fe = 0,5F0
(при β ® ¥, D Im ® 0 ). При β → 0 , т. е. при L → 0 , F ® Fe ,
Im →1. Таким образом, изменение внешнего потока при заданном
2Ic
β приведет к изменению максимального критического тока; Im ми-
нимален при |
Fe |
= 0,5 и максимален (| Im |= 2Ic ) при |
Φe |
= 0 и |
|
|
|
F0 |
|
Φ0 |
|
Φe |
= 1. |
|
|
|
|
Φ0 |
|
|
|
|
|
9 |
10 |
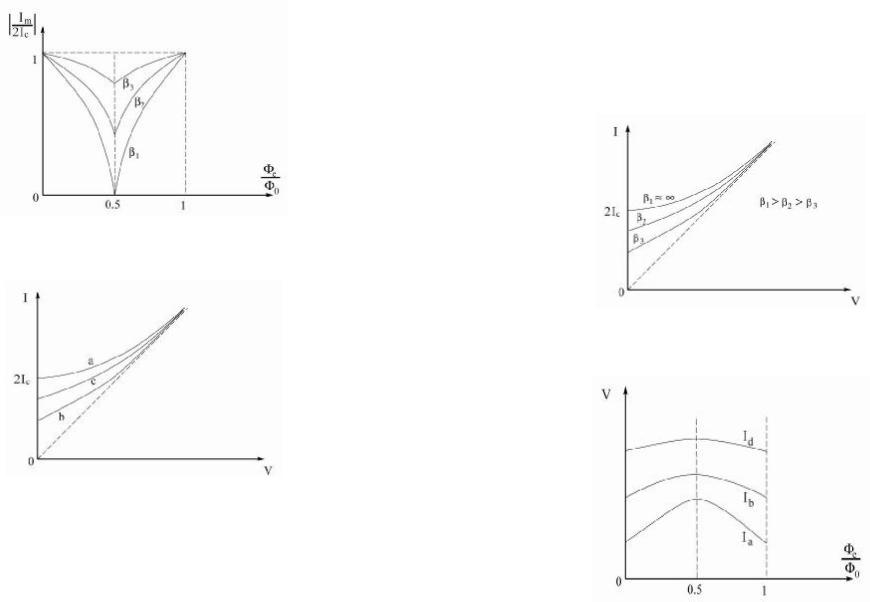
Рис. 4. Зависимость максимального сверхтока Im
от внешнего потока при различных значениях β : β1 < β2 < β3
|
Рис. 5. ВАХ dc-сквида при β = const : |
|||
Fe |
= 0 (или 1) (a); |
Fe |
= 0,5 (b); 0 < Fe <1, но |
Fe ¹ 0,5 (c) |
F0 |
|
F0 |
|
F0 |
Вольт-амперная характеристика (ВАХ) сквида при заданном
β ¹ 0 и Φe = 0 имеет вид, изображенный на рис. 5 (a). При Fe =1
F0
ВАХ совпадает с предыдущей ВАХ (а). При Fe = 0,5 ВАХ лежит
F0
ниже всех остальных ВАХ при тех же значениях β (b) , т.е. ВАХ при
всех остальных значениях Φe лежат между ВАХ a и b.
Φ0
Рис. 6. ВАХ dc-сквида при Φe = const
и различных значениях β ( β1 > β2 > β3 )
Рис. 7. Вольтпотоковая характеристика dc-сквида (Ia<Ib<Ic)
11 |
12 |

При заданном внешнем потоке Fe ВАХ изменяется при изме- нении β . ВАХ при β ® 0 будет лежать ниже всех остальных ВАХ при неизменном Fe , а при β ® ¥ выше всех остальных, так что все остальные ВАХ при β ¹ 0 и ∞ будут лежать между ними. Как сле-
дует из рис. 3 и 4, сверхток минимален при |
F |
и |
Fe |
, равном 0,5. |
|||
F0 |
|||||||
|
|
F0 |
|
|
|
||
Следовательно, поскольку ток смещения I = const, |
то при |
F |
и |
||||
|
|||||||
F0 |
|||||||
Fe = 0,5 будет максимальный квадратичный ток, т.е. будет макси-
F0
мальным и напряжение на сквиде. На рис. 7 представлен типичный вид вольтпотоковых характеристик dc-сквида при различных токах смещения.
æ |
¶V |
ö |
|
ç |
÷ |
||
|
|||
Как видно из рис. 7, чувствительность сквида S = ç |
|
÷ |
|
è |
¶Fe øI |
||
уменьшается при увеличении тока смещения. Оценку чувствитель- ности можно произвести по приближенной формуле:
S » |
DV |
|
I =const = |
2rDIm |
, |
(31) |
|
|
|||||||
F0 / 2 |
|
||||||
|
|
|
F0 |
|
|||
где r = R2 – динамическое сопротивление двух параллельно соеди-
ненных переходов. При β = 1: D Im » F2L0 и
S » |
r |
. |
(32) |
|
|||
|
L |
|
|
Для r ≈ 1 Ом, L »10−9 Гн , V ≈1 мкВ и S » 2мкВ / F0 .
Общие указания к выполнению работы
Данная лабораторная работа реализована в виде комплекса программ, предназначенных для расчета вольтамперных, вольтпото-
ковых характеристик и чувствительности симметричного сквида при различных значениях параметра β и тока смещения I. Дополни- тельно, вольтамперные характеристики сквида могут быть рассчита- ны при различных значениях внешнего магнитного потока Fe . В
работе используется следующий алгоритм расчета: численно реша- ется система уравнений, моделирующая динамику симметричного сквида во внешнем магнитном поле. Полученное решение позволяет найти среднее (усреднение проводится по периоду джозефсоновских осцилляций) напряжение на сквиде как функцию от величины внеш- него магнитного потока, проходящего через сквид при различных значениях тока смещения и параметра β . Чувствительность сквида
определяется как относительная глубина модуляции вольтпотоковой характеристики (зависимость среднего напряжения на сквиде от внешнего магнитного потока).
Все программы объединены в рамках одного командного фай- ла и доступны через общее меню. Далее приведены общие указания по использованию данного программного продукта.
1.Для разделения основания и мантиссы при вводе вещественных чисел используйте знак «точка», например: «–1,23», «0,567» и т.п.
2.Для набора значений параметра вводите список значений в одно поле редактирования через пробел, например: «0,01 0,1 1».
3.Для указания пределов изменения параметра введите начальное (меньшее) значение в левое поле редактирования, конечное (большее) – в правое поле.
4.Для изменения параметров алгоритма решения системы уравне- ний ПТ-СКВИДа используйте диалог «Настройки», появляю- щийся при нажатии кнопки «Настройки».
5.Для начала процесса счёта нажмите кнопку «Старт».
6.По мере выполнения вычислений на экран будет выводиться информация о проценте готовности. Напряжение на выходе ПТ-
13 |
14 |
СКВИДа как функция времени, найденное в процессе решения системы дифференциальных уравнений с текущими параметра- ми, выводится в окне «Осциллограф».
7.Каждому параметру должно быть присвоено значение.
8.Для построения семейства кривых (например, семейство ВПХ при разных значениях параметра β) введите в поле редактирова- ния соответствующего параметра нужный набор значений. При этом в полях редактирования других параметров должно содер- жаться одно и только одно значение.
9.Все значения параметров необходимо вводить в безразмерном виде. Результаты вычислений также представляются в безраз- мерном виде.
10.Для того чтобы выделить построенный график в отдельном ок- не, нажмите кнопку «Выделить». После этого появится возмож- ность редактировать график, добавлять или убирать подписи к кривым и осям, изменять тип линий, сохранять график в файл в векторных и растровых форматах.
11.Для изменения параметров алгоритма решения системы уравне- ний ПТ-СКВИДа используйте диалог «Настройки», появляю- щийся при нажатии кнопки «Настройки».
12.Для изменения точности вычислений служит ползунок «Уро- вень точности». Возможно задать уровень от 1 до 10. Уровень 1 соответствует минимальной точности и минимальному интерва- лу интегрирования, 10 – максимальной точности и максималь- ному интервалу интегрирования. Чем выше уровень точности, тем дольше идёт процесс счёта.
13.Для задания количества точек на одной кривой введите целое число в поле редактирования «Количество точек».
14.Выберите используемый алгоритм решения ОДУ из списка «Ал- горитм».
Ход работы Построение вольтпотоковой характеристики (ВПХ)
симметричного ПТ-СКВИДа.
1.Введите интервал изменения значений потока Фе внешнего маг- нитного поля, пронизывающего контур квантования ПТ-СКВИДа в поле «Фе=».
2.Введите значения параметров: I (ток смещения) и β.
3.Для построения семейства кривых при разных значениях I введи- те набор значений тока смещения в поле «I=».
4.Для построения семейства кривых при разных значениях пара- метра β введите набор значений в поле «β=».
5.Для начала счёта нажмите кнопку «Старт».
6.Ожидайте окончания счёта. Информация о текущем состоянии процесса счёта отображается на экране.
7.Для того чтобы выделить построенный график в отдельном окне, нажмите кнопку «Выделить».
Построение вольтамперной характеристики (ВАХ) симметричного ПТ-СКВИДа.
1.Введите интервал изменения значений тока смещения I в поле
«I=».
2.Введите значения параметров: Фе (поток внешнего магнитного поля) и β.
3.Для построения семейства кривых при разных значениях Фе, вве- дите набор значений потока в поле «Фе=».
4.Для построения семейства кривых при разных значениях пара- метра β, введите набор значений в поле «β=».
5.Для начала счёта нажмите кнопку «Старт».
6.Ожидайте окончания счёта. Информация о текущем состоянии процесса счёта отображается на экране.
7.Для того чтобы выделить построенный график в отдельном окне, нажмите кнопку «Выделить».
15 |
16 |
|
|
ЛАБОРАТОРНАЯ РАБОТА № 2 |
|
|
|
Построение кривой функции отклика симметричного |
Исследование асимметричного dc-сквида |
|
|
|
ПТ-СКВИДа. |
|
|
|
|
Зависимость от параметра β |
Сквиды ({SQUID} – Superconductinq Quantum Intenreference |
||
1. |
Введите интервал изменения значений параметра β в поле «β=». |
Device) – сверхпроводящие квантовые интерферометры – представ- |
||
2. |
Для построения семейства кривых при разных значениях I введи- |
ляют собой высокочувствительные датчики для измерения сверхсла- |
||
|
те набор значений тока смещения в поле «I=». |
бых магнитных полей. Обычно в литературе рассматривают симмет- |
||
3. |
Для начала счёта нажмите кнопку «Старт». |
ричные dc-сквиды [1–3]. Однако на практике изготовить абсолютно |
||
4. |
Ожидайте окончания счёта. Информация о текущем состоянии |
симметричный сквид практически невозможно из-за влияния боль- |
||
|
процесса счёта отображается на экране. |
шого числа факторов в технологии, приводящих к неоднородности и |
||
5. |
Для того чтобы выделить построенный график в отдельном окне, |
поэтому к асимметрии |
плеч сквида. Между тем |
асимметрия |
|
нажмите кнопку «Выделить». |
dc-сквида играет важную роль при работе сквида: чем больше асим- |
||
|
Зависимость от тока смещения I |
метрия, тем меньше чувствительность сквида. Кроме того, наличие |
||
1. |
Введите интервал изменения значений тока смещения I в поле |
асимметрии приводит к более эффективному возбуждению в сквиде |
||
|
«I=». |
динамического шума, обусловленного нелинейностью системы. |
||
2. |
Для построения семейства кривых при разных значениях пара- |
Цель настоящей лабораторной работы – исследование асим- |
||
|
метра β введите набор значений в поле «β=». |
метричной модели dc-сквида, влияние асимметрии на вольтампер- |
||
3. |
Для начала счёта нажмите кнопку «Старт». |
ные и вольтпотоковые характеристики на чувствительность сквида. |
||
4. |
Ожидайте окончания счёта. Информация о текущем состоянии |
|
|
|
|
процесса счёта отображается на экране. |
Уравнения асимметричного dc-сквида |
|
|
5. |
Для того чтобы выделить построенный график в отдельном окне, |
Уравнение асимметричного dc-сквида, так же как и симмет- |
||
|
нажмите кнопку «Выделить». |
ричного, основывается на двух соотношениях Джозефсона: |
||
|
Литература |
I = Ic sin ϕ, |
(1) |
|
|
|
∂ϕ = 2eV , |
|
|
1. |
Шмидт В.В. Введение в физику сверхпроводников. М.: Наука, |
h |
(2) |
|
|
1982. |
|
∂t |
|
|
где I – сверхпроводящий ток куперовских пар; Ic – критический ток |
|||
2. |
Бароне А., Патерно Дж. Эффект Джозефсона. М.: Мир, 1984. |
|||
3. |
Кларк Дж. Сверхпроводящие квантовые интерференционные |
джозефсоновского перехода; ϕ – разность фаз волновой функции |
||
|
приборы для низкочастотных измерений // Слабая сверхпрово- |
сверхпроводящего конденсата на переходе; V – разность потенциа- |
||
|
димость. Квантовые интерферометры и их применения / Под ред. |
лов двумя берегами перехода. Уравнение (1) определяет стационар- |
||
|
Б.Б. Шварца, С. Фонера. М.: Мир, 1980. |
ный эффект Джозефсона, а уравнение (2) – нестационарный. Схема |
||
|
|
асимметричного dc–сквида представлена на рис. 1. |
|
|
17 |
18 |
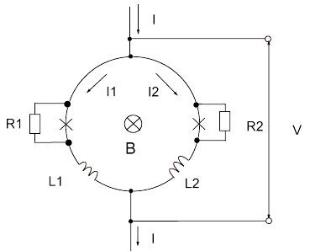
Рис. 1. Схема dc-сквида |
|
Полный ток смещения I представляются в виде: |
|
I = I1( t ) + I2( t ) = const, |
(3) |
где I1(t) и I2(t) – зависящие от времени токи в левом и правом плечах сквида соответственно. Эти токи определяются следующими выра- жениями:
I ( t ) = I |
c1 |
sinϕ ( t ) + |
V1( t ) |
|
+ I |
1 f |
( t ), |
(4) |
|||
|
|
||||||||||
1 |
1 |
|
|
R1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
I2( t ) = Ic2 sinϕ2 |
( t ) + |
V2( t ) |
+ I2 f ( t ), |
(5) |
|||||||
|
|||||||||||
|
|
|
|
|
R2 |
|
|
|
|
|
|
где Ic1 и Ic2, ϕ1 и ϕ2, V1(t) и V2(t), R1 и R2, I1f(t) и I2f(t) – критические токи, разности фаз, разности потенциалов, активные сопротивления,
шумовые токи соответственно на правом и левом плечах перехода. Шум, учитываемый в (4) и (5), как мы будем предполагать, это соб- ственные шумы сквида. Используя второе уравнение Джозефсона,
запишем для каждого из плеч
¶ϕ1 |
= |
2e |
V ( t ), |
(6) |
|
||||
¶t |
|
h 1 |
|
|
|
¶ϕ2 |
= |
2e |
V ( t ). |
|
|
(7) |
||
|
¶t |
h |
|
|
|||||
|
|
2 |
|
|
|
||||
Полная разность потенциалов на сквиде: |
|
|
|
||||||
V( t ) = V1( t ) + L1 |
dI1( t ) |
= V2( t ) + L2 |
dI2( t ) |
. |
(8) |
||||
|
dt |
|
|
dt |
|||||
Здесь L1 и L2 – индуктивности левого и правого плеча сквида. Раз- ность ϕ2(t) – ϕ1(t) определяется, как известно, полным потоком, сце- пленным с контуром квантования сквида F(t)
ϕ |
( t ) -ϕ ( t ) = 2π F( t ) |
, |
(9) |
|
2 |
1 |
F0 |
|
|
|
|
|
|
|
где F0 =ph/e – квант потока. Поток F(t) определяется в свою очередь
выражением
F( t ) = Fe( t ) - L1I1( t ) + L2I2( t ), |
(10) |
где Fe(t) – внешний поток. Введем выражение для кругового тока в контуре:
|
|
J( t ) = |
L2I2( t ) - L1I1( t ) |
, |
|
|
|
|
|
|
|
|
(11) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где L = L1+L2 – индуктивность контура сквида. С помощью (3) мож- |
|||||||||||||||||||||||||||||||||
но записать выражение для кругового тока в виде: |
|
|
|
|
|||||||||||||||||||||||||||||
|
J( t ) = |
|
L2I - LI1( t ) |
= |
- L1I + LI2( t ) |
, |
|
|
|
(11’) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
откуда получаем |
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dJ( t ) |
= - |
dI1( t ) |
, |
|
dJ( t ) |
= |
dI2( t ) |
. |
|
|
|
|
|
(12) |
||||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
dt |
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|||||
С учетом (12) выражения для V(t) можно записать в виде |
|
|
|||||||||||||||||||||||||||||||
V( t ) = V ( t ) - L |
dJ( t ) |
= V ( t ) + L |
|
|
dJ( t ) |
. |
(13) |
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
1 |
|
|
|
dt |
|
|
2 |
|
2 |
|
|
|
dt |
|
|
||||||||||
Отсюда, используя (6) и (7), легко получить: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
h |
æ dϕ ( t ) |
|
|
|
dϕ |
2 |
( t ) ö |
L - L dJ( t ) |
|
|
|||||||||||||||||||||
V( t ) = |
|
|
ç |
|
1 |
|
|
+ |
|
|
|
|
|
|
÷ + |
|
2 |
|
1 |
|
|
|
|
|
. |
(14) |
|||||||
|
|
|
dt |
|
|
dt |
|
|
2 |
|
|
|
|
dt |
|||||||||||||||||||
|
|
4e è |
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
||||||||||||||||
19 |
20 |
