
Прохождение излучения через границу раздела однородных изотропных сред (96
..pdfCopyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
Московский государственный технический университет имени Н.Э. Баумана
И.И. Пахомов, А.М. Хорохоров
ПРОХОЖДЕНИЕ ИЗЛУЧЕНИЯ ЧЕРЕЗ ГРАНИЦУ РАЗДЕЛА ОДНОРОДНЫХ ИЗОТРОПНЫХ СРЕД
Рекомендовано редсоветом МГТУ им Н Э Баумана в качестве учебного пособия. . .
по курсу «Основы оптики»
Москва Издательство МГТУ им. Н.Э. Баумана
2006
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
УДК 535.(075.8) |
|
|
ББК 22.34 |
|
|
П21 |
Рецензенты: Б.И. Голубь, Л.Н. Тимашова |
|
|
||
П21 |
Пахомов И.И., Хорохоров А.М. |
|
Прохождение излучения через границу раздела однород- |
||
|
ных изотропных сред: Учеб. пособие. – |
М.: Изд-во МГТУ |
|
им. Н.Э. Баумана, 2006. – 42 с.: ил. |
|
ISBN 5-7038-
Рассмотрены явления возникающие при падении электро магнитной волны на границу, раздела однородных изотропных- сред Проанализированы два наиболее важных с практической позиции. случая границы раздела диэлектрик диэлектрик и диэлектрик металл Приведен вывод: уравнений– Френеля ам плитудных и– энергетических. коэффициентов отражения и ,про- пускания Особое внимание уделено поляризационным пре- образованиям. волны при отражении от границы раздела и про- хождении через нее -
Для студентов . го курса обучающихся по направлению Оптотехника 3- , « Ил. 14. Библиогр». . 6 назв.
ISBN 5-7038-
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
1. ПРОХОЖДЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ |
||||||||
ЧЕРЕЗ ГРАНИЦУ РАЗДЕЛА ОДНОРОДНЫХ |
||||||||
ДИЭЛЕКТРИЧЕСКИХ СРЕД |
|
|||||||
1.1. |
Уравнения Френеля |
|
||||||
Рассмотрим поведение плоской электромагнитной волны, пада- |
||||||||
ющей на границу раздела двух сред со значениями диалектрической |
||||||||
проницаемости ε1,, ε2, магнитной проницаемости μ1, μ2 |
по обе сто- |
|||||||
роны от границы раздела. |
|
|
|
|
|
|
|
|
Если на границу раздела двух однородных сред, обладающих |
||||||||
разными оптическими свойствами, падает плоская волна, она раз- |
||||||||
деляется на две волны: проходящую во вторую среду и отраженную. |
||||||||
Существование этих волн вытекает из граничных условий. Можно |
||||||||
показать, что они удовлетворяются при наличии как проходящей, |
||||||||
так и отраженной волн. Предположим, что эти волны также являют- |
||||||||
ся плоскими, и выведем выражения для их амплитуд и направлений |
||||||||
распространения. |
|
|
|
|
|
|
|
|
Обозначим величины, относящиеся к падающей волне, индек- |
||||||||
сом (i), к отраженной и прошедшей — |
индексами (r) и (t) соответ- |
|||||||
ственно. |
|
|
|
|
|
|
|
|
Уравнения падающей, прошедшей и отраженной волн запишем |
||||||||
в комплексной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
~(i) |
|
|
|
|
|
~rS |
|
|
|
|||
E~ (i) = E~0(i) |
∙ exp "i(ωit − ωi |
|
|
|
+ δi)# ; |
|
||
|
|
V1 |
|
|||||
|
|
|
|
|
~(r) |
|
||
E~ (r) = E~0(r) |
∙ exp "i(ωrt − ωr |
~rS |
|
+ δr)# ; |
(1.1) |
|||
|
|
|||||||
V1 |
|
|||||||
|
|
|
|
|
~(t) |
|
|
|
|
|
|
~rS |
|
|
|
||
E~ (t) = E~0(t) |
∙ exp "i(ωtt − ωt |
|
|
+ δt)# , |
|
|||
|
V2 |
|
||||||
|
|
|
|
|
|
|
|
3 |
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
где E0 |
, |
E0 |
, E0 |
— |
|
|
амплитуды колебаний электрического векто- |
||||||||||||||||||||||||||||||||
~ (i) |
|
~ (r) |
~ |
(t) |
|
|
|
|
|
|
частоты колебаний волн; δ(i), δ(r), δ(t) — |
||||||||||||||||||||||||||||
ра в волнах; ωi, ωr, ωt — |
|
||||||||||||||||||||||||||||||||||||||
начальные фазы волн; S |
|
, |
S |
(r) |
, S |
|
|
|
|
— |
|
единичные векторы, харак- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
~(i) |
|
~ |
|
~(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
скорости рас- |
||||||||||
теризующие направления распространения; V1, V2 — |
|
||||||||||||||||||||||||||||||||||||||
пространения волны в средах 1 |
|
и |
|
2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
V1 = √ |
c |
|
|
; V2 = √ |
|
c |
|
. |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
ε1μ1 |
ε2μ2 |
|
|
|
|
|
||||||||||||||||||||||||||||
Введем комплексные амплитуды волн |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
~ |
|
~ (i) |
e |
iδi |
; |
|
|
~ |
|
|
~ |
(t) |
e |
iδt |
; |
|
|
|
|
|
~ |
|
|
~ (r) |
e |
iδr |
(1.2) |
||||||||||
|
|
A = E0 |
|
|
|
|
|
T = E0 |
|
|
|
|
|
|
|
R = E0 |
|
|
|||||||||||||||||||||
и обозначим переменные части аргументов волновой функции |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~(i) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~rS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
τi = ωit − ωi |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
(r) |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~rS |
|
|
|
|
|
|
|
|
(1.3) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τr = ωrt − ωr V1 |
; |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~(t) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~rS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
τt = ωtt − ωt |
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
V2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Тогда уравнения волн примут вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
~ (i) |
|
~ |
|
iτi |
; |
|
|
~ |
|
(r) |
|
|
|
|
~ |
|
|
|
iτr |
; |
|
|
|
|
~ (t) |
~iτt |
. |
(1.4) |
|||||||||
|
|
E |
= Ae |
|
|
|
|
E |
|
|
= Re |
|
|
|
|
|
|
E |
= T |
|
|||||||||||||||||||
Воспользуемся граничным условием для напряженностей элек- |
|||||||||||||||||||||||||||||||||||||||
трического поля |
|
|
|
|
|
~ (i) |
|
|
|
~ (r) |
]τ |
|
|
|
|
|
|
~ (t) |
]τ , |
|
|
|
|
(1.5) |
|||||||||||||||
|
|
|
|
|
|
|
[E |
|
+ E |
|
|
= [E |
|
|
|
|
|
||||||||||||||||||||||
которое говорит о том, что тангенциальные составляющие полей в |
|||||||||||||||||||||||||||||||||||||||
средах 1 |
и 2 равны. Тогда с учетом |
(1.4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
~ |
|
iτi |
|
|
|
~ |
iτr |
]τ |
|
|
|
|
|
~ |
|
|
|
iτt |
]τ . |
|
|
|
|
(1.6) |
|||||||||
|
|
|
|
|
[Ae |
|
|
+ Re |
|
|
|
|
= [T e |
|
|
|
|
|
|
||||||||||||||||||||
Равенство (1.6) должно выполняться для всех значений τi, τr, |
|||||||||||||||||||||||||||||||||||||||
τt, т. е. для любого момента времени t |
и любой точки с радиусом- |
||||||||||||||||||||||||||||||||||||||
вектором ~r на границах раздела. Покажем, |
что для обеспечения это- |
||||||||||||||||||||||||||||||||||||||
го равенства необходимо, |
чтобы соблюдалось условие |
τi = τr = τt. |
|||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
Действительно, левую часть выражения (1.6) можно предста- |
||||||||||||
вить в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
iτi |
|
~ |
iτr |
= ae |
i(τi+δi) |
+ be |
i(τr+δr) |
, |
(1.7) |
z = (A)τ e |
|
+ (R)re |
|
|
|
|||||||
где a = (E0 |
)τ ; b = (E0 |
)τ — |
тангенциальные составляющие ам- |
|||||||||
~ (i) |
|
|
|
~ (r) |
|
|
|
|
|
|
|
|
плитуд колебаний падающей и отраженной волн. |
|
|
6= τr |
|||||||||
Покажем, что модуль m комплексного числа (1.7) при τi |
||||||||||||
будет зависеть от t |
и ~r. Это противоречит условию (1.6), |
поскольку |
||||||||||
правая часть в (1.6) |
представляет собой комплексное число с посто- |
|||||||||||
янным модулем: |
|
|
|
|
|
|
|
|
|
|
|
|
m2 = zz = a2 + b2 + 2ab cos[(τi − τr) + δi − δr].
Для того чтобы обеспечить независимость m от t и r, необходи- |
|
мо положить τi = τr = τ, тогда из (1.6) получим |
|
(A~ + R~)τ e−iτi = (T~)τ e−iτt , |
(1.8) |
откуда следует, что τi = τt. |
|
Таким образом, мы доказали, что переменные части аргументов |
|
волновой функции волн должны быть равными, т. е. |
|
τi = τr = τt = τ, |
(1.9) |
и, следовательно, граничное условие (1.6) будет связывать лишь |
||
комплексные амплитуды волн: |
|
|
~ ~ |
~ |
(1.10) |
(А + R)τ |
= (T )τ . |
|
Это очень важный вывод, который позволяет нам значительно упро- |
|
стить решение поставленной задачи. |
|
Поместим начало координат в плоскости раздела сред. Посколь- |
|
ку выражение (1.9) справедливо для всех ~r и t, рассмотрим точку |
|
r = 0. С учетом (1.3) и (1.9) получим ωit = ωrt = ωtt = ω, откуда |
|
ωi = ωr = ωt = ω, |
(1.11) |
|
5 |

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
т. е. частота электромагнитной волны при отражении и преломле- |
|||||||||||||||||||||
нии не изменяется. Рассмотрим теперь условие (1.9) |
в некоторый |
||||||||||||||||||||
момент времени t0. С учетом |
(1.3) и (1.11) оно имеет вид |
|
|
|
|||||||||||||||||
|
|
|
|
~(i) |
|
~(r) |
|
|
|
~(t) |
|
|
|
|
|
||||||
|
|
|
|
~rS |
|
|
= |
~rS |
|
= |
|
~rS |
. |
|
|
(1.12) |
|||||
|
|
|
|
V |
|
|
|
V |
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
1 |
|
|
|
V |
2 |
|
|
|
|
|
|
||
|
Выберем в плоскости |
P (рис. 1) |
начало координат (точка O) та- |
||||||||||||||||||
кое, что для радиуса-вектора |
~r некоторой точки О0 плоскости вы- |
||||||||||||||||||||
|
|
|
~ |
(i) |
= 0, |
т. е. ~r |
|
~ |
(i) |
, тогда из (1.12) получим |
|||||||||||
полняется условие ~rS |
|
|
S |
|
|
||||||||||||||||
~ |
(r) |
~(t) |
|
|
|
|
|
|
|
|
|
|
|
~ |
(i) |
~(r) |
~ |
(t) |
) |
||
~rS |
|
= ~rS |
= 0. Cледовательно, все три вектора (S |
|
, S |
, S |
|
||||||||||||||
перпендикулярны одному радиусу-вектору ~r и находятся в одной |
|||||||||||||||||||||
плоскости Q, |
нормальной к P . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рис. 1. Взаимное расположение плоской границы раздела сред (Р), плос-
|
|
|
|
~(i) |
|
~(r) |
кости падения (Q) и единичных векторов падающей S |
, отраженной S |
|||||
~(t) |
волн |
|
|
|
|
|
и прошедшейS |
|
|
|
будем называть |
||
|
|
~(i) |
~(r) |
~(t) |
||
Направления единичных векторов S |
, S |
, S |
|
|||
лучами. Введем систему координат xyz, в которой ось ox совпадает |
||||||
с линией пересечения плоскостей Q и Р, |
а оси oz и oy находятся в |
|||||
плоскостях Q и |
Р |
соответственно (ось oy направлена по радиусу- |
||||
вектору ~r, а ось oz |
совпадает с направлением нормали ~n к плоскости |
|||||
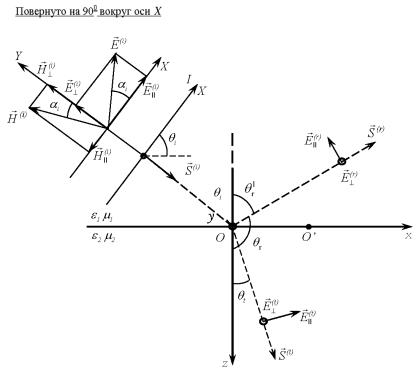
Плоскость будем называть плоскостью падения Совме стимP . теперь плоскостьQ (xoz) падения xoz с плоскостью чертежа .(рис. 2).-
6
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
Рис. 2. К выводу законов отражения, преломления и формул Френеля |
|
||||||||||||||||
|
Проекции векторов S |
|
|
, S |
, S |
на выбранные оси равны: |
|
||||||||||
|
|
|
|
~ |
(i) |
~(r) |
|
~(t) |
|
|
|
|
|
||||
|
|
|
~ |
(i) |
{sin θi |
, 0, cos θi} ; |
|
|
|||||||||
|
|
|
S |
|
|
|
|
|
|||||||||
|
|
|
~ |
(r) |
{sin θr, 0, cos θr} ; |
(1.13) |
|||||||||||
|
|
|
S |
|
|
|
|
|
|||||||||
|
|
|
~ |
(t) |
{sin θt, 0, cos θt} . |
|
|
||||||||||
|
|
|
S |
|
|
|
|
|
|||||||||
|
В связи с тем, что (1.12) справедливо для всех точек плоскости |
||||||||||||||||
P , выберем в ней точку O0, для которой |
~r = xi~, |
тогда из (1.12) по- |
|||||||||||||||
лучим |
|
|
|
x sin θi |
|
|
|
x sin θr |
|
|
|
||||||
|
|
|
|
|
= |
, |
|
|
|||||||||
т е |
|
− |
|
|
|
|
V1 |
|
|
|
V1 |
|
|
Последнее равен |
|
||
. sin θi = sin (π |
r |
|
|
|
|
|
r |
, |
откуда |
|
r |
- |
|||||
. |
|
θ0 ) = sin θ0 |
|
|
|
θ0 = θi. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
ство известно как закон отражения угол падения равен углу отра жения : -
Из.второго равенства (1.12) получим соотношение
|
|
|
|
|
x sin θi |
= |
|
x sin θt |
, |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
V1 |
|
|
V2 |
|
|
|
|
|||||||
из которого вытекает известный закон преломления. Действитель- |
||||||||||||||||||||
но, |
|
sin θi |
|
|
V1 |
|
cV1 |
|
|
|
√ |
|
|
|
n2 |
|
|
|||
|
|
|
|
|
|
|
|
ε2μ2 |
|
|
(1.14) |
|||||||||
|
|
|
= |
|
|
|
= |
|
|
= |
|
|
= |
|
. |
|||||
|
|
sin θt |
|
|
V2 |
cV2 |
|
√ |
|
n1 |
||||||||||
|
|
|
|
|
ε1μ1 |
|||||||||||||||
Из закона преломления следует, что если n2 > n1, |
то θt < θi, а если |
|||||||||||||||||||
n2 < n1, то |
θt > θi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Во втором случае может наблюдаться так называемое полное |
||||||||||||||||||||
внутреннее отражение, |
при котором преломленный луч движется |
|||||||||||||||||||
вдоль границы раздела θt = π/2. |
Соответствующий этому случаю |
|||||||||||||||||||
угол θi = θ |
называется предельным углом полного внутреннего |
|||||||||||||||||||
отражения, |
причем |
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
(1.15) |
|||
|
|
|
|
|
|
sin θпр |
= |
. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||||
При θi > θпр уравнение (1.14) не имеет решения в области дей- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
ствительных значений углов θt. Перейдем к нахождению амплитуд |
||||||||||||||
колебаний волн. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим некоторую плоскость I, перпендикулярную падаю- |
||||||||||||||
щему лучу, т. е. представляющую собой волновой фронт падающей |
||||||||||||||
волны. Очевидно, что векторы E |
(i) |
и |
H |
(i) |
падающей волны лежат |
|||||||||
|
|
|
~ |
|
~ |
|
|
|
|
|
|
|||
в этой плоскости. Введем в эту плоскость систему координат XOY |
||||||||||||||
таким образом, чтобы ось OX находилась в плоскости падения, а |
||||||||||||||
ось OY была параллельна оси Oy (см. |
рис. 2). Пусть падающая вол- |
|||||||||||||
на линейно-поляризована и вектор |
E |
(i) |
составляет азимутальный |
|||||||||||
угол αi с осью OX. Вектор H |
|
~ |
|
|
|
|
|
|
и |
|||||
перпендикулярен вектору E |
(i) |
|||||||||||||
выражается через вектор |
E |
|
~ (i) |
|
|
|
|
|
|
|
~ |
|
||
|
|
следующим образом [1, 2]: |
|
|
|
|||||||||
|
~ |
(i) |
|
|
|
|
|
|
|
|
|
|
|
|
H~~(i()i)= p |
|
S~(i) × E~ (i). |
|
|
(1.16) |
|||||||||
ε1/μ1 |
(i) |
|
||||||||||||
Разложим вектор E |
на две составляющие: Ek |
, находящуюся |
||||||||||||
в плоскости падения, и E(i), ортогональную ей (см. рис. 2): |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E(i) = E(i) cos αi; |
E(i) = E(i) sin αi; |
(1.17) |
||||||||||||
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
аналогично поступим и с вектором H |
|
: |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˉ (i) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
(i) = H(i) sin αi; |
|
H(i) |
= H(i) cos αi. |
|
|
(1.18) |
||||||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначим на чертеже также параллельные и перпендикуляр- |
||||||||||||||||||||||||
ные компоненты векторов отраженной и прошедшей волн |
(E(r), |
|||||||||||||||||||||||
E(r), |
E(t), |
E(t) |
|
). Найдем амплитуды отраженной и прошедшей |
||||||||||||||||||||
волн, используя граничные условия для векторов E |
|
|
|
|
k |
|
||||||||||||||||||
и H. Эти усло- |
||||||||||||||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
~ |
|
|
|
|
|||
вия в проекциях на оси ox и oy выглядят так: |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
Ex(i) + Ex(r) = Ex(t); |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
Ey(i) + Ey(r) = Ey(t); |
|
|
|
|
|
(1.19) |
|||||||||||
|
|
|
|
|
|
|
Hx(i) + Hx(r) = Hx(t); |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
Hy(i) + Hy(r) = Hy(t). |
|
|
|
|
|
|
|
|
|||||||||
Для того чтобы решить систему уравнений (1.19), воспользу- |
||||||||||||||||||||||||
емся соотношением (1.16), которое для всех рассматриваемых волн |
||||||||||||||||||||||||
можно записать в общем виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
H~ (j) = q |
|
S~(j) × E~ (j), |
|
|
|
|
(1.20) |
|||||||||||||||
где j = i, r, t. |
|
εj/μj |
|
|
|
|
||||||||||||||||||
В выражении (1.20) εi |
= εr |
= ε1 |
, μi |
= μr |
= μ1, εt |
= ε2, |
||||||||||||||||||
μt = μ2 |
, S |
(j) |
— |
|
единичные векторы волн, |
определяемые соотно- |
||||||||||||||||||
шением |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(1.13), |
|
~ |
(j) |
{sin θj |
, 0, cos θj} , |
|
|
|
|
(1.21) |
||||||||||||||
причем |
|
|
|
|
|
S |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
sin θr = sin θi; |
|
cos θr |
= − cos θi. |
|
|
|
(1.22) |
||||||||||||
Амплитуды E |
|
|
|
|
|
|||||||||||||||||||
|
принимают конкретные значения: при j = i E |
(i) |
= |
|||||||||||||||||||||
= Ae |
|
|
|
~ |
(j) |
|
= Re |
|
; |
при j = t |
E |
= T e |
|
. |
~ |
|
||||||||
|
; при j = r E |
|
|
|
|
|
||||||||||||||||||
~ |
iτi |
|
|
|
|
|
~ (r) |
|
~ |
iτr |
|
|
|
|
|
|
~ (t) |
|
~ |
iτt |
|
|
|
|
Запишем проекции векторов всех волн через перпендикулярные |
||||||||||||||||||||||||
и параллельные составляющие (см. |
рис. 2 ): |
|
|
|
|
|
|
|
|
|||||||||||||||
Ex(j) = Ek(j) cos θj; |
Ey(j) = E(j); |
Ez(j) = −Ek(j) sin θj. |
(1.23) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
|
Из (1.20) для векторов |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
H всех волн найдем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
H~ (j) = |
r |
εj |
|
|
|
sin θi |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
cos θj |
|
|
|
|
|
|
|
|
|
(1.24) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
μj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E(j) cos θj |
|
|
E(j) |
|
|
E(j) sin θj |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− || |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
компоненты векторов |
~ |
|
|
|
~ |
в (1.19). С |
|||||||||||||||||||||||||||||||||||||
|
Подставим теперь |
|
E и |
|
H |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
учетом соотношений (1.20)—(1.24) |
|
и условия на границе раздела |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
τi = τr = τt |
получим окончательно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
Ak cos θi − Rk cos θi |
= Tk cos θt; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
A + R = T ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.25) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
A |
√ |
|
|
cos θi |
− |
R |
|
|
√ |
|
|
cos θi = |
|
T |
|
√ |
|
|
cos θt; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
ε1 |
|
|
ε1 |
|
ε2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
√ε1A + √ε1R = √ε2T . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.25) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μ |
|
= μ |
|
= 1 |
|
|
|||||||||||||||||
|
Система |
уравнений |
|
|
|
|
|
|
|
|
|
|
записана для случая |
|
|
1 |
|
|
|
2 |
|
|
|
и |
||||||||||||||||||||||||||||||||||||||||||
легко решается относительно амплитуд |
|
~ |
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
R и |
T : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Tk = |
|
|
|
|
|
2n1 cos θi |
|
|
|
|
|
|
Ak |
= |
|
|
|
|
2 sin θt cos θi |
|
|
|
|
|
Ak; |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
n2 cos θi + n1 cos θt |
sin(θt + θi) cos(θi − θt) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
T |
|
= |
|
|
|
|
|
2n1 cos θi |
|
|
|
|
|
|
A |
|
|
|
= |
|
2 sin θt cos θi |
A |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
n1 cos θi + n2 cos θt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
sin(θi + θt) |
|
|
|
|
|
|
|
|
|
|
|
|
(1.26) |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n1 cos θi − n2 cos θt |
|
|
|
|
|
|
|
|
|
|
tg(θi − |
θt) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
R |
k |
|
= |
|
A |
k |
= |
|
A |
k |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n2 cos θi + n1 cos θt |
|
|
|
|
|
|
|
tg(θi + θt) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
R |
|
|
= |
|
n1 cos θi − n2 cos θt |
A |
|
= |
|
|
sin(θi − θt) |
A . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
n1 cos θi + n2 cos θt |
|
|
|
|
|
−sin(θi + θt) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Здесь n1 = √ |
|
; n2 = √ |
|
|
. Уравнения (1.26) — |
|
|
это уравнения Фре- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ε1 |
ε2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
неля. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на |
|
||||
|
Коэффициенты |
t |
k |
|
|
|
|
Tk |
; t |
|
= |
|
T |
|
; r |
k |
|
|
|
|
|
Rk |
; r |
|
= |
R |
- |
|||||||||||||||||||||||||||||||||||||||
|
|
= A |
k |
|
|
|
|
A |
|
|
|
|
= A |
k |
|
|
|
A |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
зываются амплитудными коэффициентами отражения и пропуска- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ния соответственно. |
Так как углы θi и θt |
вещественны, |
амплитуд- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ные коэффициенты также вещественны, |
и, |
следовательно, фаза ка- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ждой компоненты отраженной и прошедшей волн равна фазе соот- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ветствующей компоненты падающей волны либо отличаются от нее |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
на π |
радиан. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
