Лабораторная работа №2

Аналитическое исследование эффективности статической балансировки загрузки мвс

1. Цель работы

Целью работы является изучение двух следующих методов статической балансировки загрузки многопроцессорной вычислительной системы (МВС) [1, 2]: 1) балансировка загрузки на основе геометрической схемы декомпозиции области решения; 2) балансировка загрузки на основе равномерной декомпозиции узлов расчетной сетки.

2. Теоретическая часть

2.1. Постановка задачи. Пусть-n-мерный вектор параметров задачи. Положим, что, где-n-мерное арифметическое пространство. Параллелепипедом допустимых значений вектора параметров назовем не пустой параллелепипед, где- заданные константы. На векторXдополнительно наложено некоторое количество функциональных ограничений, формирующих множество, где- непрерывные ограничивающие функции. На множестве тем или иным способом (аналитически или алгоритмически) определена вектор-функциясо значениями в пространстве. Ставится задача поиска значения некоторого функционала.

Положим, что приближенное решение поставленной задачи может быть найдено по следующей схеме.

Шаг 1. Покрываем параллелепипедПнекоторой сеткой(равномерной или неравномерной, детерминированной или случайной) с узлами.

Шаг 2. В тех узлах сетки, которые принадлежат множеству ,вычисляем значения вектор функции.

Шаг 3. На основе вычисленных значений вектор функциинаходим приближенное значение функционала.

В виде рассмотренной схемы можно представить, например, решение задачи вычисления многомерного определенного интеграла от функции в области.

Суммарное числоарифметических операций, необходимых для однократного определения принадлежности вектораXмножеству(т.е. суммарную вычислительную сложность ограниченийи ограничивающих функций), обозначим. Вообще говоря, величиназависит от вектораX. Мы, однако, пренебрежем этой зависимостью, и будем полагать, что имеет место равенство. Заметим, что до начала вычислений величина, как правило, неизвестна. Однако в процессе первого же определения принадлежности некоторого узла сеткимножеству ,эту величину можно легко определить (с учетом предположения о независимости этой величины от вектораX). Поэтому будем полагать величинуизвестной.

Неизвестную вычислительную сложность вектор-функции обозначим. Подчеркнем зависимость величиныот вектораX. Величинаудовлетворяет, во-первых, очевидному ограничению. Во-вторых, положим, что известно ограничение сверху на эту величину, имеющее смысл ограничения на максимально допустимое время вычисления значения. Вычислительную сложностьназовем вычислительной сложностью узла,.

Вычислительную сложность генерации сетки положим равной, а вычислительную сложность конечномерной аппроксимации функционала- равной, где(дзета) - общее количество узлов сетки, принадлежащих множеству .Положим, что при данныхвеличины- известные константы.

В качестве вычислительной системы рассмотрим однородную МВС с распределенной памятью, состоящую из процессоров иhost-процессора, имеющих следующие параметры:

• – время выполнения одной арифметической операции с плавающей запятой;

• - диаметр коммуникационной сети;

• l – длина вещественного числа в байтах;

• – латентность коммуникационной сети;

• – время передачи байта данных между двумя соседними процессорами системы без учета времени.

В качестве меры эффективности параллельных вычислений используем ускорение

,

где - время последовательного решения задачи на одном процессоре системы,- время параллельного решения той же задачи наNпроцессорах,- номер метода балансировки. Будем рассматривать также в качестве меры эффективности параллельных вычислений асимптотическое ускорение

,

где - время параллельного решения задачи наNпроцессорах без учета коммуникационных расходов (когда).

2.2. Статическая балансировка загрузки методом равномерной декомпозиции параллелепипеда П. Для балансировки загрузки при решении рассматриваемой задачи можно использовать различные методы статической и динамической балансировки загрузки. Простейшим является статический метод на основе декомпозиции параллелепипедаПнаравных подобластей и назначении каждой из этих подобластей своему процессору. Назовем данный метод балансировки методом равномерной декомпозиции параллелепипедаП. Для двумерного случаяэтот метод балансировки иллюстрирует рис. 1.

Балансировка загрузки методом декомпозиции параллелепипеда Почень проста в реализации. Однако она может быть малоэффективной в следующем случае:

• объем пересечения параллелепипеда Пи множества(т.е. объем множества) невелик по сравнению с объемом параллелепипедаП;

• вычислительная сложность значительно превышает вычислительную сложность.

При этом некоторые из подобластей могут не содержать вовсе или содержать малое количество узлов сетки, принадлежащих множеству, и процессоры МВС, которым распределены такие подобласти, будут значительное время простаивать.

Рис. 1. К балансировке загрузки методом равномерной декомпозиции параллелепипедаП

Введем следующие обозначения:

• - множество узлов сетки, покрывающих подобласть,;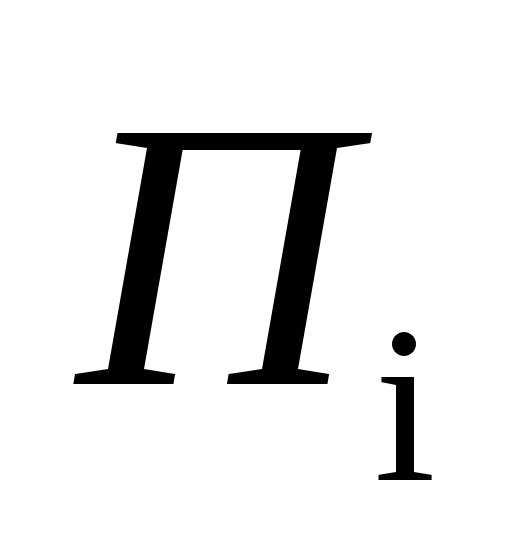

• ,- число узлов во множестве,, а- символ ближайшего целого большего;

• ,- число узлов сетки, принадлежащих множеству;

• ,,- узлы сетки, принадлежащие множеству;

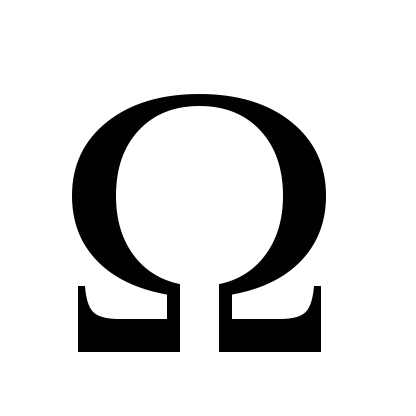• - общее число узлов сетки, принадлежащих множеству;.

В этих обозначениях схему параллельных вычислений при решении рассматриваемой задачи с использованием балансировки загрузки методом равномерной декомпозиции параллелепипеда Пможно представить в следующем виде.

Шаг 1. Host-процессор выполняет следующие действия:

• строит сетку ;

• плоскостями, параллельными одной из координатных плоскостей, разбивает ее узлы на множества ;

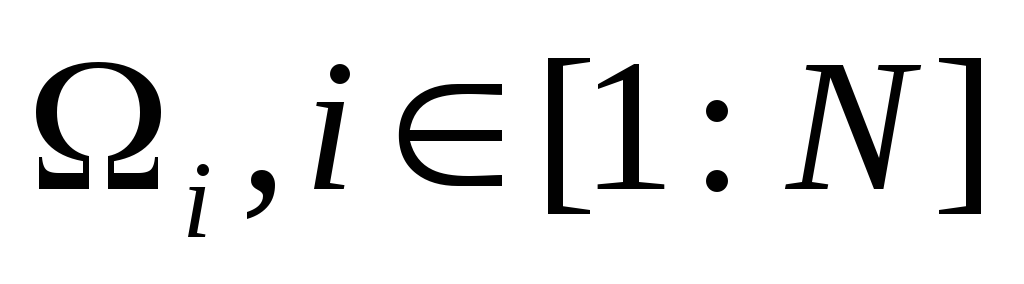• передает процессору 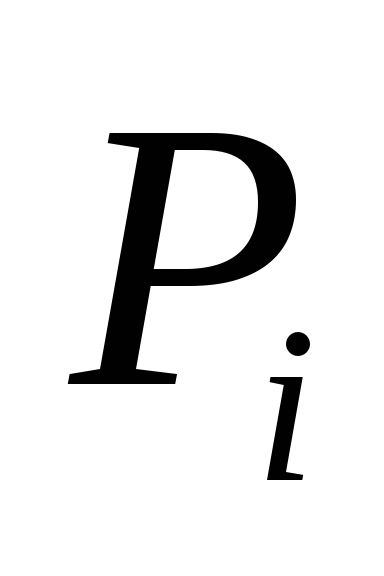координаты узлов множества.

Шаг 2. Процессорвыполняет следующие действия:

• принимает от host-процессора координаты узлов множества;

• последовательно для всех узлов этого множества определяет их принадлежность множеству;

• вычисляет в каждом из узлов множествазначение вектор-функции;

• передает host-процессорувычисленных значений и заканчивает вычисления.

Шаг 3. Host-процессор выполняет следующие действия:

• принимает от процессоров ,вычисленные ими значения вектор-функции;

• на основе полученных значений вектор-функциивычисляет приближенное значение функционала.

Очевидна модификация балансировки загрузки методом равномерной декомпозиции параллелепипеда П, при которой множество узловстроится неhost-процессором, а процессором,. При этомhost-процессору достаточно передать процессорулишь границы «его» подобласти. За счет распараллеливания процедуры генерации расчетной сеткии, возможно, меньшего количества обменов следует ожидать, что эффективность такого метода балансировки будет выше, чем эффективность метода равномерной декомпозиции параллелепипедаП. Отметим, что указанная модификация рассматриваемого метода возможна лишь в том случае, когда можно отказаться от централизованной генерации расчетной сетки.

Можно предложить и другую модификацию метода равномерной декомпозиции параллелепипеда П, направленную на повышение его эффективности. Разделим областьна подобласти,таким образом, чтобы их объемы пересечений с множествомбыли примерно одинаковы. Если при этом использовать равномерную сетку, то ее количество узлов в каждой из подобластей, в отличие от исходной схемы метода декомпозиции параллелепипедаП, будет примерно одинаковым. Если множествоимеет сложную топологию, то построение такого разбиения областина подобласти может иметь неприемлемо высокую вычислительную сложность.

В соответствии с изложенной схемой балансировки загрузки методом равномерной декомпозиции параллелепипеда П, время решения задачи на процессореможно оценить величиной

,, (1)

где сумма представляет собой вычислительную загрузку процессора, а сумма- его коммуникационную загрузку. Отсюда следует, что время параллельного решения всей задачи равно

. (2)

Аналогично, время решения задачи на одном процессоре равно

. (3)

2.3. Статическая балансировка загрузки методом равномерной декомпозиции расчетных узлов. Положим, что из числаузлов расчетной сеткимножествупринадлежитузлов. Обозначим. Тогда идею рассматриваемого метода балансировки загрузки можно представить в следующем виде (рис. 2):

• среди всех узлов сеткивыделяемузлов;

• разбиваем узлы намножеств,, где множествосодержит узлы, множество- узлыи т.д.

• назначаем для обработки процессору множеств узлов,.

Очевидно, что если величина не кратна количеству процессоров, то количество узлов во множествах,,,может отличаться (не более чем на единицу). Для простоты записи пренебрежем этим обстоятельством.

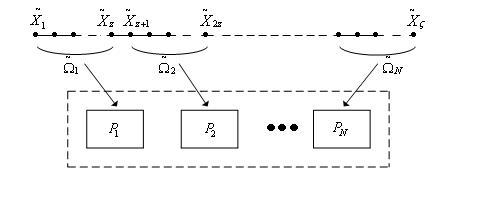
Рис. 2. К балансировке загрузки методом 2.

Назовем рассматриваемый метод балансировки методом равномерной декомпозиции расчетных узлов. Отметим, что в этом случае естественна централизованная генерация расчетной сетки (наhost-процессоре).

Схему параллельных вычислений при балансировке загрузки методом равномерной декомпозиции расчетных узлов можно представить в следующем виде.

Шаг 1. Host-процессор выполняет следующие действия:

• строит сетку ;

• среди всех узлов сеткивыделяетузлов;

• разбивает узлы намножеств узлов;

• посылает процессору координаты узлов множества.

Шаг 2. Процессорвыполняет следующие действия:

• принимает от host-процессора координаты узлов множества;

• вычисляет в каждом из этих узлов значение вектор-функции ;

• передает host-процессорувычисленных векторов и заканчивает вычисления.

Шаг 3. Host-процессор выполняет следующие действия:

• принимает от процессоров ,вычисленные ими значения вектор-функции;

• на основе полученных значений вектор-функциивычисляет приближенное значение функционала.

Обозначим ,,- узлы сетки, принадлежащие множеству. Тогда при балансировке загрузки методом равномерной декомпозиции расчетных узлов время решения задачи на процессореможно оценить величиной

, (4)

где слагаемое представляет собой вычислительную загрузку процессора, а слагаемые- его коммуникационную загрузку. Таким образом, время параллельного решения всей задачи оценивается величиной

. (5)

Заметим, что вычислительная загрузка процессора в данном случае не включает в себя определение принадлежности узлов сеткимножеству- эта работа выполняетсяhost-процессором.

Как и при использовании балансировки загрузки методом равномерной декомпозиции параллелепипеда П, в данном случае время решения задачи на одном процессоре определяется формулой (3).