Энергия волны

Упругая среда, в которой распространяются механические волны, обладает как кинетической энергией колебательного движения частиц, так и потенциальной энергией, обусловленной деформацией.

Выбрав малый объём среды dV можно записать для плотности энергии

, где

–скорость колеблющихся частиц в среде;

–фазовая скорость волны;

–плотность среды;

–относительная деформация.

Для продольной плоской волны и, т.е.

.

Для плоской гармонической волны

.

Для сферической гармонической волны

.

Среднее за период значение плотности энергии

.

Скорость переноса энергии равна фазовой скорости .

Потоком энергии через малую площадкуназывают отношение.

Так как , то

, где

–вектор плотности потока энергии или вектор Умова.

т.е. поток энергии через произвольную поверхность S , мысленно проведённую в среде, охваченной волновым движением, равен потоку вектора Умова через эту поверхность.

Скалярную величину I , равную модулю среднего значения вектора Умова, называют интенсивностью волны:

Принцип суперпозиции волн : результирующее возмущение в какой либо точке линейной среды при одновременном распространении в ней нескольких волн равно сумме возмущений, соответствующей каждой из этих волн в отдельности.

.

Интерференция волн

Две волны называют когерентными, если разность их фаз не зависит от времени. Гармонические упругие волны, частоты которых одинаковы, когерентны всегда.

Рассмотрим наложение двух гармонических волн, возбуждаемых в однородной и изотропной среде точечными источниками S₁ и S₂ , с циклическими частотами ω₁ = ω₂ = ω и начальными фазами φ₁ и φ_2..

По принципу суперпозиции

.

А и Ф определяем по методу векторных диаграмм

.

–геометрическая разность хода волн от S₁ и S₂ до точки М.

Амплитуда результирующих колебаний максимальна еслиили

. Если то.

Амплитуда результирующих колебаний минимальна еслит.е.или

. Если то.

Число т называют порядком интерференционного максимума.

Стоячие волны

Частным случаем интерференции волн являются стоячие волны, которые образуются в результате наложения двух бегущих синусоидальных волн, распространяющихся навстречу друг другу и имеющих одинаковые частоты и амплитуды, а в случае поперечных волн ещё и одинаковую поляризацию.

Тогда

.

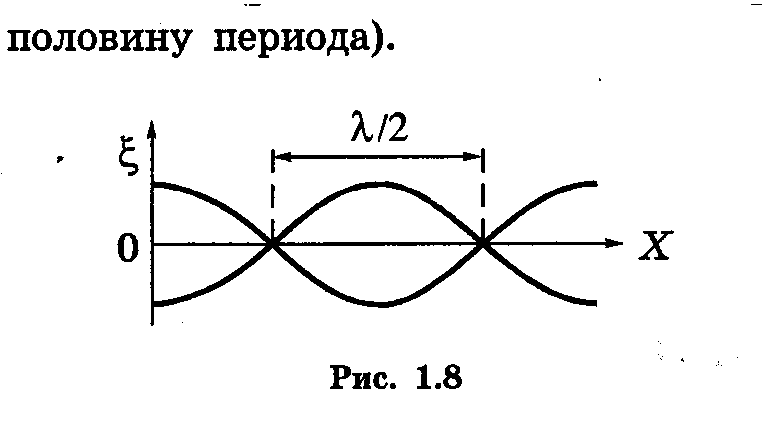
Амплитуда стоячей волны является периодической функцией от координатых .

Точки, в которых А_СТ = 0 называют узлами стоячей волны, а точки, где А_СТ = 2А называют пучностями стоячей волны.

Положение узлов и пучностей находится из условий

–узлы;

–пучности (т = 0; 1; 2; …).

Длиной стоячей волны называют расстояние между двумя соседними узлами или двумя соседними пучностями

.

В стоячей волне все точки между двумя узлами колеблются с различными амплитудами, но с одинаковыми фазами (синфазно), т.к. аргумент синуса в уравнении стоячей волны не зависит от координаты х .

В стоячей волне скорость колебательного движения частиц среды

,

а относительная деформация среды

.

Таким образом, в отличие от бегущей волны, в стоячей волне опережаетυ₀ по фазе на π/2 , так что в те моменты времени, когда υ₀ достигает амплитудного значения, обращается в нуль, и наоборот.

В пучностях стоячей волны располагаются пучности скорости частиц и узлы деформации среды.

Если l – длина струны, стержня или столба газа, υ – фазовая скорость волны, а λ – её длина, то для струн или стержней, закреплённых на обоих концах, и столбов газа в трубах, закрытых или открытых с обоих концов, на длине l укладывается целое число длин стоячей волны λ_СТ = λ /2.

Отсюда вытекает условие

–собственные частоты колебаний таких систем (гармоники).

–основной тон;

–первый обертон.

Для стержней, один конец которых закреплён, а другой свободен, и для труб, закрытых с одного конца и открытых с другого,

.