
Теория функций комплексного переменного (120
..pdfCopyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
Московский государственный технический университет имени Н.Э. Баумана
А.В. Копаев, В.И. Леванков, А.В. Мастихин
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Методические указания к выполнению домашнего задания
Москва Издательство МГТУ им. Н.Э. Баумана
2012
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
УДК 517.53 ББК 22.161.8 К65
|
Рецензент О.Д. Алгазин |
|
К65 |
Копаев А. В. |
|
Теория функций комплексного переменного : метод. ука- |
||
|
зания к выполнению домашнего задания |
/ А. В. Копаев, |
|
В. И. Леванков, А. В. Мастихин. – М. : |
Изд-во МГТУ |
им. Н. Э. Баумана, 2012. – 38, [2] с. : ил.
Представлены необходимые теоретические сведения. Приведены примеры решения задач по теории функций комплексного переменного. Даны условия домашнего задания.
Для студентов второго курса IV семестра, изучающих теорию функций комплексного переменного.
Рекомендовано Учебно-методической комиссией НУК ФН МГТУ им. Н.Э. Баумана.
УДК 517.53 ББК 22.161.8
c МГТУ им. Н.Э. Баумана, 2012
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
1. ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ, ЗАДАННЫМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ
Комплексным числом z называют выражение вида z = x+yi, где x, y — любые действительные числа; i — символ, называемый мнимой единицей. Действительные числа x и y соответственно называют действительной и мнимой частями комплексного числа z и обозначают
x = Re z;y = Im z.
Символы Re и Im являются начальными буквами латинских слов realis (действительный) и imaginarius (мнимый). Представление комплексного числа z = x+yi называют алгебраической формой записи комплексного числа. Если y = 0, то комплексное число x+0i считается совпадающим с действительным числом x; если же x = 0, то комплексное число 0+yi обозначается yi и называется чисто мнимым. Два комплексных числа z = x+yi и w = u+vi равны тогда и только тогда, когда равны их действительные и мнимые части, т. е. z = w тогда и только тогда, когда x = u и y = v.
Комплексное число z = x+yi изображается на плоскости точкой с координатами (x;y) в прямоугольной декартовой системе координат или ее радиус-вектором. Плоскость в этом случае называют плоскостью комплексного переменного, а координатные оси — осями действительных и мнимых переменных и соответственно обозначают Re и Im.
Комплексно-сопряженным к числу z = x+yi называют число z¯= x−iy, изображаемое точкой (и вектором), симметричной точке (и вектору) z относительно действительной оси (рис. 1).
3

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
Рис. 1
Суммой комплексных чисел z и w называют комплексное число
z +w = (x+u)+(y +v)i.
Произведением комплексных чисел z и w называют комплексное число
zw = (xu−yv)+(xv +yu)i.
Однако запоминать эти формулы нет надобности. Так как сложение и умножение комплексных чисел коммутативны, ассоциативны и связаны дистрибутивным законом, сложение и умножение комплексных чисел в алгебраической форме выполняется по обычным правилам алгебры с заменой произведения ii (которое обозначается i2) на −1 (основное свойство символа i: i2 = −1). Операции сложения и умножения комплексных чисел обратимы. Разность комплексных чисел z и w вычисляется по формуле
z −w = (x−u)+(y −v)i.
Таким образом, и вычитание комплексных чисел в алгебраической форме осуществляется по обычным правилам алгебры. Частное комплексных чисел z и w вычисляется по формуле
z x+iy xu+yv yu−xv w = u+iv = u2 +v2 + u2 +v2 i.
Запоминать эту формулу также нет надобности. Необходимо запомнить правило деления комплексных чисел в алгебраической
4

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
форме: для вычисления частного wz следует числитель и знаме-
натель этой дроби умножить на число w¯, сопряженное комплексному числу w, поскольку ww¯ = (u+vi)(u−vi) = u2 +v2. Таким образом,
wz = wzww¯¯.
Отметим, что действия сложения и вычитания комплексных чисел в алгебраической форме соответствуют действиям сложения и вычитания векторов, изображающих эти числа на плоскости комплексных чисел.
Пример 1. Даны комплексные числа z = 2−i и w = 3+4i. Вычислить: 1) z +w; 2) z −w; 3) zw; 4) wz .
Решение. 1)z + w = (2 −i) + (3 + 4i) = (2 + 3) + (−1 + 4)i = = 5+3i;
2)z −w = (2−i)−(3+4i) = (2−3)+(−1−4)i = −1−5i; 3)zw = (2−i)(3+4i) = 6−3i+8i−4 = 6+5i+4 = 10+5i;
4) |
z |
= |
2−i |
= |
(2−i)(3−4i) |
= |
6−3i−8i−4 |
= |
2−11i |
= |
|
w |
|||||||||||
|
|
3+4i |
(3+4i)(3−4i) |
|
9+16 |
|
25 |
|
|||
=0,08−0,44i.
Взаключение определим степень комплексного числа с целым показателем: zn = zz ...z (n сомножителей); z0 = 1 (z =);0
z−n = z1n (z =).0
Пример 2. Для комплексного числа z = 3−2i найти: 1) z2; 2) z3.
Решение. 1)z2 = (3−2i)2 = 9−12i−4 = 5−12i; 2)z3 = (3−2i)3 = 27−54i−36+8i = −9−46i.
2. ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ, ЗАДАННЫМИ В ТРИГОНОМЕТРИЧЕСКОЙ ФОРМЕ
При изучении свойств комплексных чисел весьма удобной оказывается их геометрическая интерпретация. Рассмотрим на плоскости комплексных чисел наряду с прямоугольной декартовой системой координат полярную систему координат, полюс которой находится в начале прямоугольной декартовой системы координат,
5
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
а полярная ось совпадает с положительной полуосью оси действительных чисел Re.
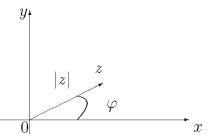
Полярный радиус ρ точки z называют модулем комплексного числа z и обозначают |z|, т. е. ρ = |z|.
Полярный угол ϕ точки z, принадлежащий промежутку (−π; π], называют аргументом комплексного числа z (главным значением аргумента) и обозначают arg z, т. е. ϕ = argz (рис. 2).
Рис. 2
Ясно, что модуль комплексного числа z = x+yi есть неотрицательное действительное число ρ = x2 +y2, причем ρ = 0 тогда и только тогда, когда z = 0. Аргумент нуля не определен, а для остальных комплексных чисел аргумент определяется следующими формулами:
argz = arctg |
y |
, если x > 0; |
|||||||||
x |
|||||||||||
|
|
|
|
|
|
y |
|
||||
argz = π +arctg |
|
,y |
если x < 0,y ≥ 0; |
||||||||
x |
|||||||||||
argz = −π +arctg |
|
, если x < 0,y < 0; |
|||||||||
x |
|||||||||||
argz = |
π |
|
, если x = 0,y > 0; |
||||||||
|
|||||||||||
2 |
|
π |
|
|
|
|
|
||||
argz = − |
|
, если x = 0,y < 0. |
|||||||||
2 |
|||||||||||
Отметим, что в некоторых учебниках считают, что значение аргумента принадлежит промежутку [0;2π).
Так как прямоугольные декартовы и полярные координаты связаны соотношениями x = ρ cos ϕ, y = ρ sin ϕ, для комплексного числа z = x+yi получаем другую форму записи:
z = x+yi = ρ cos ϕ +iρ sin ϕ, или z = ρ(cos ϕ +isin ϕ).
6

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
Эту форму представления комплексного числа называют тригонометрической.
Пусть даны два комплексных числа в тригонометрической форме:
z1 = ρ1(cos ϕ1 +isin ϕ1) и z2 = ρ2(cos ϕ2 +isin ϕ2).
При умножении комплексных чисел их модули перемножаются, а аргументы складываются:
z1z2 = ρ1 ρ2 cos(ϕ1 + ϕ2)+isin(ϕ1 + ϕ2) .
При делении комплексных чисел их модули делятся, а аргументы вычитаются:
z1 |
= |
ρ1 |
cos(ϕ1 |
− ϕ2)+isin(ϕ1 |
− ϕ2) . |
z2 |
ρ2 |
Правило умножения двух комплексных чисел в тригонометрической форме распространяется на любое число сомножителей. В частности, если все сомножители равны,
zn = ρn(cosnϕ +isinnϕ), n = 1,2,...
Эту формулу называют формулой Муавра (она справедлива и для любого целого отрицательного числа n).
|
Пример 3. Для комплексного числа z = 1−i найти z10. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
π |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Решение. Легко видеть, что |z| = |
|
|
2, а argz = − |
|
(рис. 3). |
||||||||||||||
|
|
|
4 |
|||||||||||||||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
10 |
|
|
π |
|
π |
|
|
|
|
|
|
|||||
z10 |
= √2 |
cos10 − |
= |
|
|
|
||||||||||||||
|
|
+isin10 − |
|
|
|
|
|
|
||||||||||||
|
4 |
4 |
|
|
|
|||||||||||||||
|
|
|
|
|
= (2)5 |
cos − |
5π |
+isin |
− |
5π |
= |
|
|
|
||||||
|
|
|
|
|
2 |
2 |
π |
|
|
|||||||||||
|
|
|
|
|
|
|
|
= 32 cos − |
π |
|
|
|
= −32i. |
|||||||
|
|
|
|
|
|
|
|
|
+isin − |
|
||||||||||
|
|
|
|
|
|
|
|
2 |
2 |
|||||||||||
В заключение введем понятие корня n-й степени из комплексного числа z. Так называют любое комплексное число w, для которого wn = z. Если z = 0, то существует единственное число w = 0, такое, что wn = z. Если же z =, 0то существует ровно n корней n-й степени из комплексного числа z = ρ(cos ϕ +isin ϕ):
√ ϕ +2πk ϕ +2πk
w = n ρ cos n +isin n , k = 0,1,2,...,n−1.
7
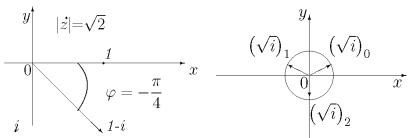
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
Из этой формулы следует, что все корни n-й степени из комплексного числа z изображаются вершинами правильного n-угольника,
вписанного в окружность радиуса с центром в начале коор- n |z|
динат.
|
|
|
|
|
|
|
|
|
Рис. 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4 |
|
|
|
|
|
|
|
|||||||||||
|
|
Пример 4. Найти все значения |
√3 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
Решение. Легко видеть, что |i| = 1, а |
argz = |
(рис. 4). По- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
этому, подставляя k = 0,1,2, получаем три значения кубического |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
корня: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
π |
|
+2π |
· |
0 |
|
|
|
|
π |
|
|
+2π |
· |
0 |
|
|
|
|
|
π |
|
π |
||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
√i 0 |
= cos |
|
|
|
|
|
|
+isin |
|
|
|
|
|
|
|
|
|
|
|
|
|
= cos |
|
|
|
+isin |
|
|
= |
|
|||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
√ |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
6 |
6 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
3 |
|
+ |
i |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
2π |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
√3 |
|
1 |
|
|
|
|
|
+ |
2π ·1 |
|
|
|
|
|
|
|
|
+ |
2π ·1 |
|
= cos |
5π |
+isin |
5π |
= |
||||||||||||||||||||||||||||||||
|
= cos |
2 |
+isin |
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
i |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
3 |
|
|
6 |
6 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
3 |
+ |
i |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
√3 |
|
|
|
|
|
|
|
+ |
2π ·2 |
|
|
|
|
π |
+ |
2π ·2 |
|
|
|
|
|
3π |
|
|
|
|
|
|
3π |
|
|
||||||||||||||||||||||||||
|
2 |
= cos |
2 |
+isin |
2 |
|
= cos |
+isin |
= −i. |
||||||||||||||||||||||||||||||||||||||||||||||||
i |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
2 |
2 |
||||||||||||||||||||||||||||||||||||||||||
8

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
3. ЗАДАНИЕ КРИВЫХ И ОБЛАСТЕЙ НА КОМПЛЕКСНОЙ ПЛОСКОСТИ
Кривые на плоскости задаются уравнениями относительно заданной системы координат, например, относительно прямоугольной декартовой системы координат — уравнением F(x;y) = 0, а относительно полярной системы координат — уравнением Φ(ρ; ϕ) = = 0. Пусть
z = x+yi = ρ(cos ϕ +isin ϕ)
— комплексное число. Тогда
x = z +2 z¯, y = z2−iz¯, ρ = |z|, ϕ = argz.
Поэтому на комплексной плоскости кривые задаются уравнениями
|
z +z¯ |
z |
z |
|
|
||
F |
|
; |
|
2−i¯ |
= 0 |
или |
Φ(|z|;argz) = 0. |
2 |
|
||||||
Приведем примеры уравнений некоторых кривых на комплексной плоскости, для получения которых не требуется выполнение тождественных преобразований, а используется лишь геометрическая интерпретация комплексных чисел.
Окружность с центром в точке z0 радиуса R задается уравнением |z −z0| = R (рис. 5), так как |z −z0| есть расстояние от точки z до точки z0.
Эллипс с фокусами в точках z1 и z2 и большой полуосью
a (2a > |z1 − z2|) задается уравнением |z − z1| + |z − z2| = 2a (рис. 6 ).
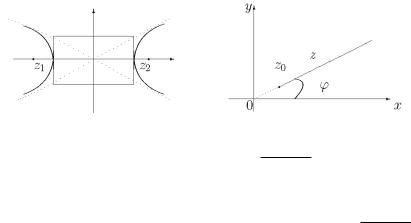
Рис. 5 |
Рис. 6 |
9
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
Рис. 7 |
Рис. 8 |
|
Отметим, что для такого эллипса c = |
|z1 −2 z2| |
, b2 = a2 −c2. |
Гипербола с фокусами в точках z1 и z2 и действительной полу- |
||
осью a (2a < |z1 −z2|) задается уравнением |z −z1|−|zz−1 z2|z2= |
|||||
|
гиперболы c |
|
|
|
, |
= 2a (рис. 7). Отметим, что для такой |
|
= |
| − |
| |
|
|
|
|
2 |
|
|
b2 = c2 −a2.
Луч с началом в точке z0, образующий угол ϕ с положительной полуосью действительной оси, задается уравнением arg(z −z0) = ϕ (рис. 8).
Так как координаты точек, не лежащих на кривой, не удовлетворяют уравнению этой кривой, области, ограниченные кривыми, задаются соответствующими неравенствами.
Например, открытый круг с центром в точке z0 радиуса R задается неравенством |z −z0| < R, замкнутый круг с центром в точке z0 радиуса R — неравенством |z −z0| ≤ R и т. п.
4. ПОНЯТИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Пусть D — некоторое множество комплексных чисел. Если каждому комплексному числу z множества D поставлено в соответствие комплексное число w, то говорят, что на множестве D
задана комплекснозначная функция w = f(z) комплексного переменного z, а множество D называют областью определения этой функции. Примерами функций комплексного переменного могут служить:
многочлен n-й степени с комплексными коэффициентами a0, a1,...,an
10
