Фазовая плоскость.

Фазовой плоскостью называется двумерное пространство, координатами в котором являются координата точки и проекция импульса (соответственно, обобщённая координата и обобщённый импульс).

Для пружинного маятника из закона сохранения энергии:

следует, что фазовая траектория точки, совершающей свободные незатухающие колебания, является эллипсом. Покажем это:

, ,

где главные полуоси эллипса равны: , .

Замечание. В случае если система состоит из N осцилляторов, то фазовое пространство имеет размерность 2N.

Векторная диаграмма.

Рассмотрим радиус-вектор точки М, вращающейся вокруг начала координат с постоянной угловой скоростью . Угол между радиус-вектором и осью Х меняется с течением времени по закону: , где ₀ – его начальное значение. Пусть длина радиус-вектора ОМ=А. Координаты точки М:

,

описывают колебания осцилляторов вдоль осей X и Y.

Данная форма представления колебаний называется амплитудной (векторной) диаграммой.

Рассмотрим сложение двух колебаний одного направления: пусть два осциллятора совершают колебания вдоль оси Х с циклическими частотами ₁ и ₂:

и .

Зададим эти колебания на векторной диаграмме с помощью векторов.

1-е колебание задаётся вектором , который вращается вокруг начала координат с постоянной угловой скоростью ₁, угол вращения меняется по закону: .

2-е колебание задаётся вектором , соответственно, угол .

Тогда результирующему колебанию сопоставим вектор с фазой .

По теореме косинусов:

.

Учтем, что ,

, тогда

,

или .

Соответственно, .

Остановимся подробнее на двух частных случаях.

1) Пусть , . Тогда .

Амплитуда результирующего колебания в этом случае не зависит от времени.

Если разность начальных фаз колебаний , где n – целое число, то и наблюдается усиление колебаний: .

Если разность начальных фаз колебаний , где n – целое число, то и колебания гасят друг друга: .

Для вывода зависимости результирующего колебания воспользуемся соотношением:

, тогда с учётом чётности функции косинуса имеем:

.

Амплитудой должно быть выражение, не зависящее от времени, но амплитуда не может быть отрицательной величиной, следовательно:

, тогда

.

Если , то , если то .

2) Рассмотрим случай, когда амплитуды одинаковые: , но частоты отличаются на небольшую величину: , , . Для упрощения примем, что и . Аналогично предыдущему случаю, получаем:

.

Пренебрегая в выражении для фазы второго сомножителя величиной по сравнению с величиной , получаем:

.

Если , то , но если , то .

Т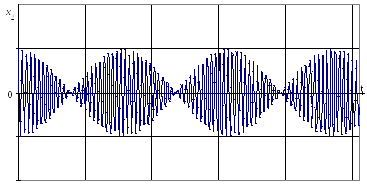 аким образом, при сложении колебаний близких частот возникает периодическое изменение амплитуды и скачкообразное изменение фазы результирующего колебания – явление, которое называется биением.

Сложение взаимно перпендикулярных гармонических колебаний

равных и кратных частот

Рассмотрим траекторию точки, совершающей колебания одновременно по двум взаимно перпендикулярным направлениям:

, .

Отметим, что в этих обозначениях при _x=_y фазы колебаний сдвинуты на /2.

1) Пусть частоты колебаний одинаковые: .

Обозначим . Получим уравнение траектории:

, ,

, ,

.

Это уравнение линии второго порядка на плоскости.

Если =0 (фазы колебаний сдвинуты на =), то получаем эллипс: .

Если = (фазы колебаний сдвинуты на =0 или ), то получаем отрезок прямой.

2) Фигуры для некоторых других соотношений частот и разности фаз показаны на рисунках.

С оотношение частот колебаний по фигуре можно определить из равенства:

,

где n – количество пересечений фигуры и прямой, параллельной соответствующей оси.

Траектория точки, совершающей одновременно два взаимно перпендикулярных колебания, при рациональном отношении частот колебаний называется фигурой Лиссажу. Условие рационального отношения частот означает, что отношение частот можно записать в виде рационального числа. В этом случае траектория является замкнутой. Если отношение частот не является рациональным числом, то траектория - незамкнутая линия.