Химическое (термодинамическое) равновесие Учебное пособие

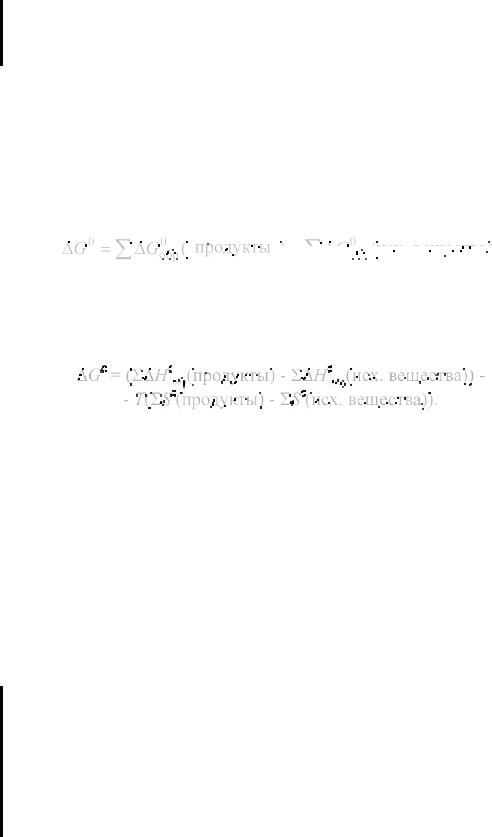
По величине (11), то есть по ∆G, судят о том, возможна ли данная химическая реакция (при р, Т = const).

Если ∆G < 0, возможна реакция в прямом направлении; если ∆G > 0, возможна реакция в обратном направлении; если ∆G = 0, в системе имеет место состояние равновесия.

С помощью уравнения (12) можно вычислить константу равновесия Kр для реакции, протекающей при температуре Т, если известно изменение стандартной свободной энергии процесса. Последняя величина может быть найдена одним из двух способов.

1)Поскольку свободная энергия Гиббса – функция состояния системы,

ееизменения в химической реакции можно вычислить, используя энергии Гиббса образования всех участников реакции:

.

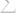
2) Учитывая связь ∆G = ∆H − T∆S, стандартное изменение энергии Гиббса можно рассчитать по стандартным энтальпиям образования и абсолютным энтропиям всех участников реакции:

Термодинамические таблицы обычно содержат энтальпии образования, свободные энергии образования и абсолютные энтропии веществ при температуре 298,15 K (25 °С) и давлении 1 бар = 105 Па (это стандартное со-

Выбранное стандартное состояние реакционной системы определяет значение константы равновесия (через ∆G0, по уравнению (12) или (13)).

При отрицательных ∆G0 константа равновесия весьма велика. Равновесное состояние системы характеризуется крайне малыми концентрациями исходных веществ и большими концентрациями продуктов реакции. При положительных ∆G0 константа равновесия весьма мала. Для равновесного состояния такой системы характерны малые концентрации продуктов реакции и большие концентрации исходных веществ.

21

Заметим, что сами величины ∆G0 к направлению конкретных реакций непосредственного отношения не имеют.

Практический расчет Kр поясним на следующем примере.

Пример 6. Рассчитайте константу равновесия Kр для реакции в газо-

вой фазе при 25 °С:

4HCl + O2 ↔ 2Cl2 + 2H2O.

Решение. Воспользуемся вторым способом расчета. Энтальпии образования Cl2(г), Н2О(г), HCl(г) и О2(г) из простых веществ в стандартных условиях соответственно равны 0; –241,82; –92,31 и 0 кДж/моль. На основе следствия из закона Гесса энтальпия реакции равна:

H2980 = [2 0 + 2 (−241,82)] − [4 (−92,31) + 0] = –114,40 кДж/моль = –114400

Дж/моль.

Абсолютные энтропии Cl2(г), Н2О(г), HCl(г) и О2(г) в стандартных услови-

ях соответственно равны 223,07; 188,83; 186,91 и 205,138 Дж/(моль.K). Та-

ким образом,

S2980 = [2·223,07 + 2·188,83] – [4·186,91 + 205,138] = –128,98

Дж/(моль.K).

Стандартная свободная энергия реакции:

G2980 = –114400 – 298,15·(–128,98) = –75945 Дж/моль.

По уравнению (13):

K p = e+75945/(8.314 298.15) = 2,02·1013 бар–1.

Примечание. Термодинамические свойства вещества можно най-

ти в [5].

Поскольку ∆G0 = ∆H0 – T∆S0, то (12) можно записать в ином виде:

Из этой формы записи следует, что при низких температурах состояние равновесия в реакционной системе преимущественно определяет энтальпийный фактор, а при высоких – энтропийный.

22

Другое преобразование уравнения (12) или (13) позволяет увидеть

связь константы равновесия с температурой и стандартной энтальпией реакции ∆Н0:

Это уравнение называется уравнением изобары Вант-Гоффа (в дифференциальной форме) . Из него следует, что константа равновесия увеличивается с температурой в эндотермических процессах: dlnKp/dT > 0, если ∆Н0 > 0. Для экзотермических процессов ∆Н0 < 0, и константа с ростом температуры уменьшается. Таким образом, уравнение (15) подтверждает принцип Ле Шателье.

Уравнению (15) часто придают особую форму, которая удобна для графической иллюстрации температурного влияния. Переписав его в виде

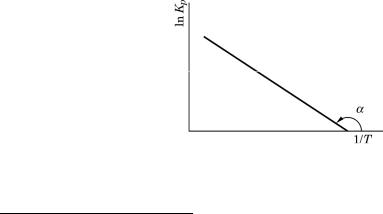
Мы заменили ∆Н0 на энтальпию реакции ∆Н, протекающей в нестандартных условиях, так как энтальпия реакции слабо зависит от давления. В небольшом температурном интервале, где ∆Н почти постоянна, уравнение (16) предсказывает линейную зависимость lnKp от обратной температуры (рис. 3). Тангенс угла наклона прямой определяет энтальпию процесса: tgα = –∆H/R.

Рис. 3. Зависимость константы равновесия от температуры для эндотермического процесса по уравнению (16)

При выводе уравнения (15) пользуются одним из важнейших уравнений термодинамики – уравнением Гиббса–Гельмгольца. Его изучают в курсах физики и физической химии.

23

Таким методом пользуются при экспериментальном определении теплот химических реакций.

4. Упражнения

1. Напишите выражения для констант химического равновесия следующих реакций (все реагирующие вещества находятся в газовой фазе):

а) СО + 2Н2 ↔ СН3ОН;

б) СН4 + 2Cl2 ↔ CH4Cl2 + 2HCl;

в) 2CO + 4H2 ↔ C2H5OH + H2O; г) 4HCl + O2 ↔ 2H2O + 2Cl2;

д) 2Н2О ↔ 2Н2 + О2; е) Н2О ↔ Н2 + 1/2О2;

ж) 1/2СОCl2 + 1/2H2O ↔ 1/2CO2 + HCl.

2. Напишите выражения для констант химического равновесия следующих реакций (реагирующие вещества находятся в разных фазах):

а) Mg(OH)2(тв) ↔ MgO(тв) + Н2О(г); б) 2HgO(тв) ↔ 2Hg(ж) + О2(г);

в) NH4Cl(тв) ↔ NH3(г) + HCl(г);

г) С(тв) + О2(г) ↔ СО2(г);

д) FeO(тв) + Н2(г) ↔ Fe(тв) + Н2О(г);

е) FeO(тв) + Н2(г) ↔ Fe(тв) + Н2О(ж).

3. В реакционной системе при 600 °С установилось равновесие

СО(г) + Cl2(г) ↔ СOCl2(г).

Отбор проб показал, что равновесные концентрации СО, Cl2 и СОCl2 оказались равными 0,0280; 0,0420 и 0,0145 моль/л соответственно. Рас-

считайте константу равновесия Kр при 600 °С.

Ответ: 12,3 (моль/л)–1.

4. На основе условия задачи 3 найдите константу равновесия Kр при

600 °С.

Ответ: 1,70·10–6 Па–1 = 0,170 бар–1 (1 бар = 105 Па).

5. В реакционной системе при Т = 900 K установилось равновесие

4HCl(г) + О2(г) ↔ 2Н2О(г) + 2Cl2(г).

24

Равновесные парциальные давления HCl, О2, Н2О и Cl2 равны 1,00; 9,73; 2,00 и 1,50 бар соответственно. Рассчитайте константы равновесия Kр

и Kс при 900 K.

Ответ: 0,925 бар–1; 69,2 (моль/л)–1.

6. Для реакции

4HCl(г) + О2(г) ↔ 2Н2О(г) +2Cl2(г)

при 900 K константа равновесия Kр = 69,2(моль/л)–1. Исходные концентра-

ции HCl, О2, Н2О и Cl2 равны 0,024; 0,15; 0,019 и 0,015 моль/л соответст-

венно. В каком направлении будет протекать реакция при 900 K?

Ответ: в прямом.

7. Для реакции

4HCl(г) + О2(г) ↔ 2Н2О(г) +2Cl2(г)

при 900 K константа равновесия Kр = 0,925 бар–1. Исходные парциальные давления HCl, О2, Н2О и Cl2 равны 0,65; 1,25; 2,00 и 2,00 бар соответственно. В каком направлении будет протекать реакция при 900 K?

Ответ: в обратном.

8. Реакционная смесь получена из 5 моль Н2 и 3 моль Cl2. Для реакции

Н2(г) + Cl2(г) ↔ 2HCl(г)

при некоторой температуре Kс = 5,000. Определите состав равновесной реакционной смеси в мольных долях. (Мольная доля i-го вещества в смеси – это отношение количества этого вещества к общему числу молей всех веществ смеси).

Ответ: 0,3785; 0,1285; 0,4930.

9. Реакционная система получена смешением 100 моль СО и 160 моль Н2О. При 727 °С константа равновесия Kс реакции

СО(г) + Н2О(г) ↔ СО2(г) + Н2(г)

составляет 1,37. Каков равновесный состав образующейся смеси (в молях) при 727 °С?

Ответ: 33,9; 93,9; 66,1 и 66,1 моль.

10. При 444 °С константа равновесия реакции

25

Н2(г) + I2(г) ↔ 2НI(г)

Kс = 46,7. Какова степень диссоциации HI при 444°С? Сколько молей Н2 нужно добавить к одному молю HI, чтобы степень диссоциации стала рав-

ной 10%?

Ответ: 22,6%; 0,297 моль.

11. При 2000 K степень диссоциации СО2 на СО и О2 составляет 0,0151, когда общее давление в системе равно 1 бар. Рассчитайте константы равновесия Kр и Kс реакции

СО2 ↔ СО + 1/2О2

при 2000 K.

Ответ: 1,31·10–3 бар1/2; 1,02·10–4 (моль/л)1/2.

12. При 2500 K и давлении 0,2 бар степень диссоциации молекулярного водорода на атомы равна 2,79 %. Рассчитайте константы равновесия Kр и Kс реакции диссоциации

Н2 ↔ 2Н

при 2500 K.

Ответ: 6,23·10–4 бар; 3,00·10–6 моль/л.

13. При 1000 K реакция

С(графит) + СО2(г) ↔ 2СО(г)

обладает константой равновесия Kр = 1,70 бар. Найдите концентрации СО2 и СО в равновесном состоянии системы при 1000 K и общем давлении 2,10 бар.

Ответ: 0,0106 и 0,0147 моль/л.

14. В химический реактор с жесткими стенками поместили измельченный графит, после чего туда ввели диоксид углерода, который при 20 °С создал давление в 1,10 бар. Реактор нагрели до 1000 K, в нем установилось химическое равновесие

С(графит) + СО2(г) ↔ 2СО(г)

с константой Kр = 1,70 бар. Рассчитайте общее давление в реакторе при

1000 K.

Ответ: 4,82 бар.

26

15. Рассчитайте константы химического равновесия реакций, протекающих в газовой фазе при 25 °С:

а) SO3 = SO2 + 1/2O2;

б) СО2 + 3Н2 = СН3ОН + Н2О;

в) 3С2Н2 = С6Н6(бензол).

Необходимые термодинамические данные возьмите из таблицы 1.

Ответ: а) 3,86·10–13 бар1/2; б) 0,212 бар–2; в) 1,66·1087 бар-–2.

16. В таблице 2 приведены значения констант равновесия для реакции

СО2(г) + Н2(г) = СО(г) + Н2О(г)

при нескольких температурах. Постройте график зависимости константы равновесия от температуры в координатах lnKp – 1/T и определите графически среднее значение энтальпии реакции в указанном температурном интервале. Сравните полученное значение с термохимическим: H2980 = +41,16

кДж/моль.

27

Библиографический список

1.Теоретические основы неорганической химии / Е. Г. Гончаров [и др.]. – Воронеж : Изд. дом ВГУ, 2014. – 589 с.

2.Гончаров Е. Г. Общая и неорганическая химия / Е. Г. Гончаров, Ю. П. Афиногенов, А. М. Ховив. – Воронеж : Изд-во ВГУ, 2010. – 404 с.

3.Карапетьянц М. Х. Общая и неорганическая химия / М. Х. Карапетьянц, С. И. Дракин. – М. : Химия, 1992. – 592 с.

4.Угай Я. А. Общая и неорганическая химия / Я. А. Угай. – М. : Высшая школа, 2007. – 527 с.

5. Краткий справочник физико-химических величин / под ред. А. А. Равделя и А. М. Пономаревой. – Л. : Химия, 1999. – 232 с.

28