
Алгебра логики
Высказывание - повествовательное предложение, относительно которого определенно и объективно можно сказать истинно оно или ложно (ЛОЖЬ или ИСТИНА, 0 или 1, TRUE или FALSE). Алгебра логики – раздел математики, изучающий процессы умозаключений и законы, которые позволяют из истинности одних высказываний делать заключения об истинности или ложности других высказываний, независимо от их конкретного содержания. Алгебра логики (булева алгебра) была создана в 1854 г. Дж. Булем и в настоящее время находит широкое применение при разработке алгоритмов и для структурно-функционального описания, анализа и синтеза современных электронных схем.
Базовыми операциями
алгебры логики служат операции логического
умножения – конъюнкции (обозначается
точкой или знаком
![]() ),
логического сложения – дизъюнкции
(обозначается знакам + или
),
логического сложения – дизъюнкции
(обозначается знакам + или![]() ),
логического отрицания – инверсии
(обозначается надчеркиванием или знаком
),
логического отрицания – инверсии
(обозначается надчеркиванием или знаком![]() ).
При составлении формул применяются
скобки, чтобы изменять порядок выполнения
операций. Наивысшим приоритетом обладает
операция инверсии, затем идет конъюнкция
и потом уже дизъюнкция.
).
При составлении формул применяются
скобки, чтобы изменять порядок выполнения
операций. Наивысшим приоритетом обладает
операция инверсии, затем идет конъюнкция
и потом уже дизъюнкция.
Таблицы истинности для указанных операций:
|
А |
|
|
0 |
1 |
|
1 |
0 |
|
|
А |
В |
А | ||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
0 |
0 |
0 | ||||||
|
|
0 |
1 |
0 | ||||||
|
|
1 |
0 |
0 | ||||||
|
|
1 |
1 |
1 | ||||||
|
|
|
|
| ||||||
|
|
|
|
| ||||||
|
|
|
|
| ||||||
|
|
|
|
| ||||||
|
|
|
|
| ||||||
|
А |
В |
А |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Представляют
интерес еще две логические операции:
эквиваленции (обозначается знаком
![]() )
и импликации (обозначается знаком
)
и импликации (обозначается знаком![]() ).
).
|
|
А |
В |
А | ||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
0 |
0 |
1 | ||||||
|
|
0 |
1 |
0 | ||||||
|
|
1 |
0 |
0 | ||||||
|
|
1 |
1 |
1 | ||||||
|
|
|
|
| ||||||
|
|
|
|
| ||||||
|
|
|
|
| ||||||
|
|
|
|
| ||||||
|
|
|
|
| ||||||
|
А |
В |
А |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Приведем основные логические законы (тождественно истинные высказывания), которые позволяют упрощать формулы, заменяя их подформулы эквивалентными выражениями:
 -
закон
тождества
-
закон
тождества - закон исключенного
третьего
- закон исключенного
третьего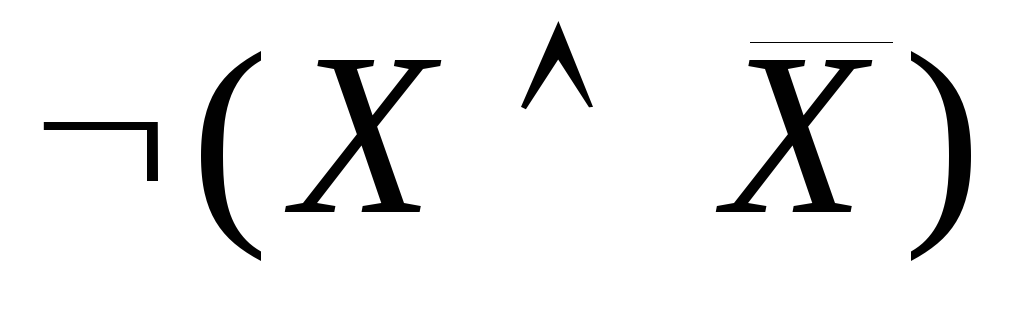 - закон противоречия
- закон противоречия -
закон двойного отрицания
-
закон двойного отрицания -
закон коммутативности конъюнкции
-
закон коммутативности конъюнкции -
закон ассоциативности конъюнкции
-
закон ассоциативности конъюнкции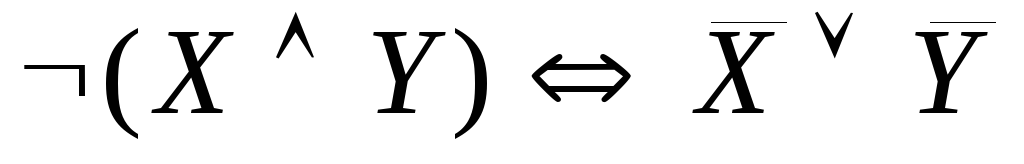 и
и
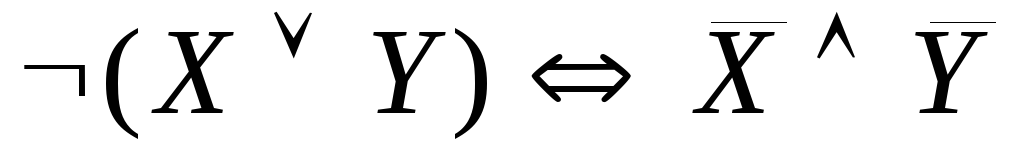 -
законы де Моргана
-
законы де Моргана и
и
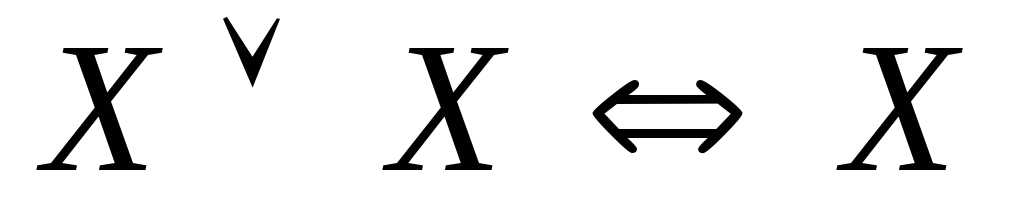 -
законы
сокращений
-
законы
сокращенийи еще с десяток тождественно истинных и тождественно ложных высказываний.
Пример 1. Упростить логическую формулу
![]()
Пример 2. Доказать законы де Моргана, построив соответствующие таблицы истинности.
-
X
Y

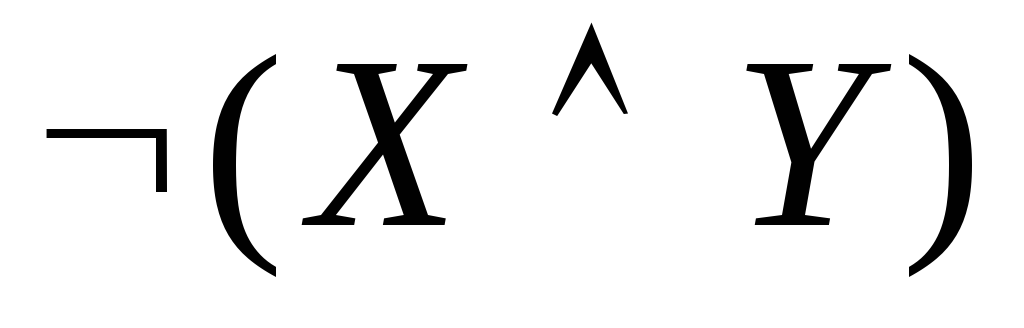



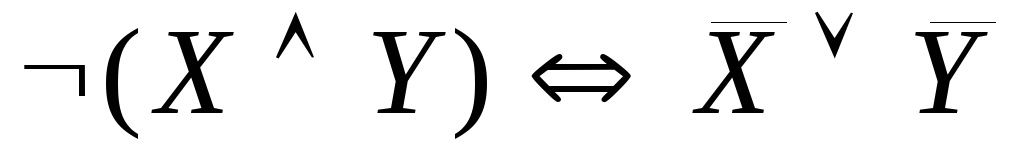
0
0
0
1
1
1
1
1
0
1
0
1
1
0
1
1
1
0
0
1
0
1
1
1
1
1
1
0
0
0
0
1
Таким образом,
результат, выражаемый последним столбцом
таблицы, свидетельствует, что высказывание
![]() является
тождественно истинным (выполняется при
любых комбинациях значений входящих в
него высказываний), т.е. оно действительно
является логическим законом. Так же
доказывается второй закон де Моргана.
является
тождественно истинным (выполняется при
любых комбинациях значений входящих в
него высказываний), т.е. оно действительно
является логическим законом. Так же
доказывается второй закон де Моргана.
