1.2. Модели потоков отказов и сбоев

Отказы и сбои, а следовательно и обусловленные ими возможные ошибки в результатах преобразований, являются случайными событиями, которые в течение некоторого интервала времени эксплуатации АСОИиУ могут произойти или не произойти и точно предсказать заранее моменты их наступления невозможно.

В то же время существуют методы оценки безотказности и достоверности функционирования АСОИиУ, основанные на случайном (вероятностном) характере поведения системы в процессе ее эксплуатации. Для этого создается математическая модель процесса эксплуатации, которая, очевидно, должна основываться на методах теории вероятностей. Так, законы распределения таких случайных величин как наработка на отказ , и наработка на сбойзадают математические модели таких эксплуатационных событий как наступление отказа или сбоя.

В реальных системах действуют различные законы распределения времени между событиями (отказами и сбоями). С целью упрощения оценки надежности обычно принимают, что отказы и сбои подчиняются экспоненциальному закону распределения, для которого плотность распределения непрерывной случайной величины (наработки на отказ, при этом; или наработки на сбой, тогда) задается выражением

, (1.1)

где параметр распределения, интерпретируемый как интенсивность потока событий: отказов, при этом, или сбоев, тогда.

Зависимость интенсивности отказов аппаратурных средств АСОИиУ от времени (характеристика) приведена на рис. 1.1. Ее можно разбить на три периода (обозначены на рисунке римскими цифрами.)

В первый – начальный период работы, именуемый периодом приработки (периодом «детства»), по мере выявления и устранения ошибок проектирования и производственных дефектов интенсивность отказов уменьшается со временем.

Рис. 1.1. Типичная характеристика

Во второй – основной период рабо-ты, обычно достаточно длительный, интенсивность отказов является наиболее низкой и остается примерно постоянной. Этот период соответствует периоду эксплуатации АСОИиУ (период «зрелости»).

В третий – заключительный период интенсивность отказов значительно увеличивается из-за физического износа (деградации) аппаратуры (период «старости») и система снимается с эксплуатации и утилизируется.

Для многих АСОИиУ этот период как правило не достигается, так как они морально устаревают раньше, чем успевают износиться.

Если интенсивность отказов , что имеет место для периода эксплуатации АСОИиУ, то можно показать, что математическое ожидание (среднее значение) интервала времени до наступления отказа (наработка на отказ)связано с параметромвыражением

. (1.2)

Аналогичная связь справедлива и для среднего значения наработки на сбой

. (1.3)

Следует также отметить, что экспоненциальное распределение связано с таким важным понятием, как пуассоновский поток событий.

Пуассоновский поток событий – поток, для которого длительность интервалов между событиями является случайной величиной, имеющей экспоненциальное распределение, задаваемое выражением (1.1).

Важное свойство пуассоновского потока событий заключается в том, что вероятность появления события в течение интервала времени определяется только длительностью интервала и интенсивностью потока событийи не зависит от предистории, т.е. от того, сколько и когда произошло событий (отказов, сбоев) в прошлом.

Интервалы времени между моментами наступления событий в пуассоновском потоке – независимые случайные величины, а вероятность того, что за время [0,t] произойдет ровно событий определяется выражением

. (1.4)

Выражение (1.4) следует интерпретировать следующим образом – число случайных событий, например, число отказов или сбоев системы в течение интервала времени [0,t] определяется дискретным распределением Пуассона с параметром

Отметим следующие свойства пуассоновского потока.

1. Пуассоновский поток ординарен – вероятность двух или более событий в момент времени практически равна нулю.

2. При наложении независимых пуассоновских потоков с интенсивностями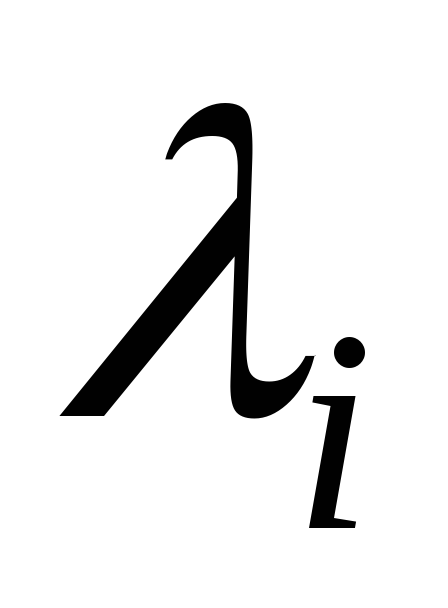() образуется пуассоновский поток с суммарной интенсивностью

. (1.5)

3. Интервал времени от случайно взятой точки до наступления очередного события в пуассоновском потоке с интенсивностью есть случайная величина, имеющая экспоненциальное распределение с тем же параметром.