2.6.2. Код Хэмминга

Развитие принципа контроля по четности приводит к корректирующему коду Хэмминга, который позволяет не только обнаруживать, но и исправлять одинарную ошибку в передаваемых по каналу связи или хранимых в ЗУ данных. Р. Хэмминг – сотрудник фирмы Bell Telephone Laboratories в 1948 г. разработал метод обнаружения и исправления одиночных ошибок в передаваемых кодовых словах. В его честь используемый код был назван кодом Хэмминга.

В коде Хэмминга из n позиций (разрядов) слова m используются в качестве информационных, а k разрядов в качестве контрольных (n=m+k).

Все информационные разряды разбиваются на k групп. За каждой группой закрепляется один контрольный разряд. Перед передачей информации в канал связи или записи её в ЗУ в контрольные разряды заносится символ 0 и 1 таким образом, чтобы сумма единиц в группе, включая контрольный разряд, стала четной. При этом контрольные символы располагают в разрядах кодового слова, номера которых равны целой степени основания 2, т.е. в первом, втором, четвертом и т.д.

Контрольная аппаратура (декодер) на выходе из канала производит k проверок на четность всех k групп. После каждой проверке в специальный k – разрядный регистр, именуемый регистром синдрома ошибки, записывается 0, если результат соответствующей проверки свидетельствует об отсутствии ошибки в разрядах проверяемой группы, и 1, если проверка выявила ошибку. Таким образом, каждая проверка заканчивается записью в соответствующие разряды регистра синдрома ошибки 0 или 1. Полученная последовательность нулей и единиц (синдром ошибки) указывает номер позиции (разряд слова) с искаженным символом.

Требуемое число контрольных разрядов и, следовательно, контрольных групп, на которое разбивают слово, определяется из следующих соображений.

Синдром ошибки должен описывать (задавать) состояния, соответствующие появлению ошибки в любом разряде n – разрядного кодового слова, а также состояние, соответствующее отсутствию ошибки.

Следовательно, должно соблюдаться соотношение:

. (2.19)

Неравенство (2.19) дает возможность определить минимальное значение k для заданного m и, следовательно, разрядность кодового слова – n.

В табл.2.8 приведены значения k и n, определенные в соответствии с (2.19) для некоторых заданных значений m.

Таблица 2.8.

m	1	2	3	4	5	6	7	8	9	10	11	12
k	2	3	3	3	4	4	4	4	4	4	4	5
n	3	5	6	7	9	10	11	12	13	14	15	17

Способ разбивки информационных разрядов на контрольные группы и определения номеров позиций контрольных разрядов следуют непосредственно из структуры ряда чисел, представленных в двоичной форме.

Рассмотрим это на следующем примере.

Предположим, что предназначенное для передачи по линии связи (или записи в память) информационное слово содержит четыре разряда, т.е. . Из таблицы 2.8 видно, что корректирующий код для этого случая должен содержать 7 разрядов (n=7), т.е. к 4 информационным должно быть добавлено 3 контрольных разряда: и (рис. 2.6).

Информационное слово Кодовое слово

7 6 5 4 3 2 1 № разряда Рис. 2.6. Преобразование информационного слова в кодовое, представленного в

коде Хэмминга (7,4)

Разбивка разрядов слова на контрольные группы производится следующим образом (рис. 2.7). В группу с номером i входят те разряды кодового слова, в двоичном номере которых в i-й позиции стоит единица. Так, в первую группу включены те разряды кодового слова, номер которых в двоичной системе счисления имеет единицу в первом разряде (1, 3, 5, 7). Вторая группа включает разряды, номера которых имеют единицу во втором разряде (2, 3, 6,7) и т.д.

Разряды 1, 2 и 4, каждый из которых принадлежит только одной контрольной группе, используется в качестве контрольных.

Рис. 2.7. Структура кодового слова и контрольных групп кода Хэмминга (7,4)

Процедуру коррекции одинарной ошибки проиллюстрируем следующим примером.

Пример 2.7. Положим, что информационное слово, подлежащее передаче или хранению, имеет вид =1100. Значения проверочных символов и , обеспечивающие четность каждой из контрольных групп, найдем из уравнений кодирования:

(2.20)

Следовательно, в канал поступит семиразрядное кодовое слово =1100001. Схема кодера, реализующего уравнения (2.20), изображена на рис. 2.8.

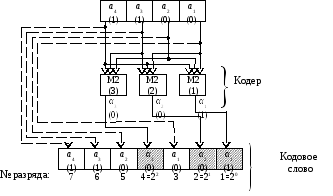
Рис. 2.8. Кодер кода Хэмминга (7, 4)

Допустим, что в канале исказился один из разрядов этого слова, например, третий, т.е. a₁. В результате на выходе из канала получим искаженное слово 11001100 (искаженный символ подчеркнут, а на рис. 2.9 – заштрихован).

Рис. 2.9. Кодовое слово и контрольные группы при искажении символа a₁

поступает на декодер (рис. 2.10), который в первую очередь проверяет сохранность четности в пределах контрольных групп.

Другими словами, декодер определяет значения разрядов синдрома S=s₃s₂s₁ по уравнениям проверок:

(2.21)

Неравенство синдрома S нулю свидетельствует об искажении кодового слова, а его значение указывает на номер искаженного разряда – S=011₂=3₁₀.

Для восстановления (коррекции) слова значение искаженного разряда нужно проинвертировать. Достигается это следующим образом. Синдром ошибки подают на дешифратор, активный выход которого возбуждает управляемый инвертор (двухвходовый элемент М2) в том разряде, в котором произошла ошибка. Если искажение кодового слова при его передаче не произошло, то все разряды синдрома ошибки будут нулями, о чем сигнализирует возбужденный нулевой выход дешифратора. Управляемые инверторы при этом пропускают принятое слово без изменений.

Рис. 2.10. Декодер кода Хэмминга

В тех случаях, когда принятые из канала слова дальше передаваться не будут и необходимость в контрольных разрядах отпадает, можно ограничиться исправлением разрядов только информационного слова и, следовательно, сократить число управляемых инверторов до четырех.

Избыточность рассмотренного варианта кода Хэмминга достаточна лишь для исправления в кодовых словах одинарных ошибок. Действительно, значение минимального кодового расстояния кода Хэмминга D_min=3 и, следовательно, согласно (2.13) код позволяет исправлять только одинарные ошибки. Если же в кодовом слове возникают две ошибки (или более), то с помощью кода Хэмминга исправить их не удается. Более того, вместо исправления двух уже возникших в канале ошибок декодером кода Хэмминга будет привнесена третья.

Проиллюстрируем сказанное на примере (рис. 2.11).

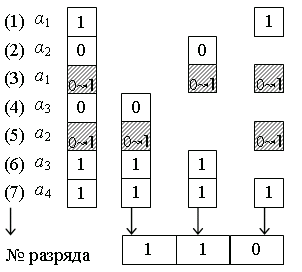
Рис. 2.11. Кодовое слово и контрольные группы при искажении символов a₁ и a₂

Предположим, что в кодовом слове =1100001 исказились два разряда, например, третий и пятый, т.е. ошибки пришлись на символы а₁ и а₂. В результате на выходе из канала получим искаженное слово =1110101(искаженные разряды подчеркнуты, а на рис. 2.11 – заштрихованы). Декодер проведет коррекцию по тем же формальным правилам – определив значение синдрома ошибки S=110₂=6₁₀, он «исправит» (проинвертирует) шестой разряд (а₃) – фактически не искаженный, и тем самым к двум имеющимся ошибкам добавиться третья. При этом формально обеспечивается условие отсутствия ошибок – восстановлена четность в пределах каждой группы и, следовательно, равенство нулю синдрома ошибки S.

От этого нежелательного эффекта можно избавиться, если использовать удлиненный код Хэмминга, способный исправлять одинарные и обнаруживать двойные ошибки, т.е. с D_min=4. Удлиненный код строится из уже рассмотренного кода Хэмминга добавлением к нему еще одного проверочного разряда , значение которого образуется таким образом, чтобы была обеспечена четность всего (n+1)-разрядного кодового слова, т.е.

(2.22)

При декодировании кодовых слов, представленных в удлиненном коде Хэмминга, к проверкам четности контрольных групп добавляется проверка четности кодового слова в целом, т.е.

(2.23)

Если предположить, что кратность ошибок в кодовых словах не превышает двух, т.е. , то возможны следующие ситуации:

d=0, тогда S=0 и P=0 (ошибок нет),

d=1, тогда S0 и P=1(ошибка исправима),

d=2, тогда S0 и P=0 (ошибки не исправимы).

Хотя удлиненный код Хэмминга и не исправляет двойные ошибки, он все же дает возможность верно интерпретировать ситуацию и не наносить ещё большего ущерба.

В рассмотренных примерах предполагалось, что ошибки произошли в информационных разрядах кодового слова. Все выше изложенное в равной степени справедливо и для случаев, когда искаженные контрольные (проверочные) разряды слова.